מבוא עדין לניתוח סיבוכיות של אלגוריתמים
Dionysis "dionyziz" Zindros <dionyziz@gmail.com>תורגם על־ידי ים מסיקה <yammesicka@gmail.com>
- English
- Ελληνικά
- македонски
- Español
- Nederlands
- עברית
- Português
- srpskohrvatski
- Українська
- Русский
- Help translate
הקדמה
הרבה מהמתכנתים שכותבים חלק מהתוכנות המגניבות והשימושיות ביותר כיום, ביניהן חלק גדול מהדברים שאנחנו רואים באינטרנט או משתמשים בהם באופן תדיר, הם אנשים ללא ידע תיאורטי במדעי־המחשב. הם עדיין אנשים די אדירים ומתכנתים יצירתיים, ואנחנו מודים להם על מה שהם בנו.
עם זאת, לתיאוריה של מדעי־המחשב יש שימושים ויישומים שיכולים להתגלות כשימושיים למדי. במאמר זה, שמיועד למתכנתים שיודעים את אומנותם אך חסרי כל רקע תיאורטי בתיאוריה של מדעי־המחשב, אני אציג את אחד מהכלים המעשיים ביותר בתחום: הסימון O גדולה, וניתוח סיבוכיות של אלגוריתמים. כמי שעבד במדעי המחשב הן במסגרת אקדמית והן בתעשייה, זהו כלי שמצאתי כאחד מהשימושיים באמת, כך שאני מקווה שאחרי שתקראו את המאמר הזה תוכלו להחיל אותו בקוד שלכם על־מנת לשפר אותו. לאחר קריאת המאמר הזה, אתם אמורים להיות מסוגלים להבין את כל המונחים הנפוצים שאנשי מדעי־המחשב משתמשים בהם כמו "O גדולה" (Big O), "התנהגות אסימפטוטית" ו"ניתוח המקרה הגרוע ביותר".
הכתוב פה גם מיועד לתלמידים בבית־ספר תיכוניים ובחטיבות הביניים, מישראל או מכל מקום אחר בעולם, המעוניינים להשתתף באולימפיאדה הבין־לאומית למדעי־המחשב, תחרות אלגוריתמים לתלמידים או תחרויות דומות אחרות. ככזה, אין לו דרישות־קדם מתמטיות והוא יספק לכם את הרקע שאתם צריכים כדי להמשיך ללמוד אלגוריתמים עם הבנה מוצקה יותר של התיאוריה מאחוריהם. כמי שנהג להתחרות בתחרויות התלמידים הללו, אני ממליץ לכם בחום לקרוא את כל חומר ההקדמה הזה ולנסות להבין אותו לחלוטין, מכיוון שהוא יהיה הכרחי כשתנסו ללמוד אלגוריתמים או טכניקות מתקדמות יותר.
אני מאמין שמה שכתוב כאן יהיה לעזר גם עבור מתכנתים מהתעשייה שאין להם יותר מדי ניסיון עם התיאוריה של מדעי־המחשב (למעשה, כמה ממהנדסי התוכנה הכי מעוררי השראה מעולם לא פקדו את מוסדות ההשכלה הגבוהה). אבל מכיוון שהמאמר הוא גם לתלמידים, לעיתים הוא ישמע קצת כמו ספר לימוד. בנוסף, חלק מהנושאים המובאים כאן עלולים להישמע מדי ברורים־מאליו עבורכם; לדוגמה, אם ראיתם אותם במהלך הלימודים שלכם בתיכון. אם אתם מרגישים שאתם יכולים להבין אותם, תוכלו לדלג עליהם. חלקים אחרים נכנסים מעט יותר לעומק, והופכים להיות טיפה תיאורטיים, שכן התלמידים בתחרויות הללו צריכים לדעת יותר על אלגוריתמים תיאורטיים מאשר העוסק הממוצע בתחום. הדברים הללו הם עדיין דברים שטוב לדעת, ולא קשה להחריד לעקוב אחריהם, כך שככל הנראה הם עדיין שווים מאוד את הזמן שלכם. מאחר שהמאמר במקור נועד לתלמידי תיכון, אין צורך ברקע מתמטי, כך שכל מי שבאמתחתו ידע בסיסי בתכנות (נניח, אם אתם יודעים מה זה רקורסיה) יוכל לעקוב ללא שום בעיה.
לאורך המאמר, תוכלו למצוא מספר הפניות המקשרות לתוכן מעניין שלעיתים קרובות יהיה מחוץ לתחום של הנושא הנידון. אם אתם מתכנתים בתעשייה, אתם ככל הנראה מכירים את הרעיונות האלו. אם אתם תלמידים מתחילים המשתתפים בתחרויות, לחיצה על הקישורים הללו תיתן לכם הכוונה לגבי אזורים במדעי־המחשב או הנדסת־תוכנה שייתכן שמעולם לא חקרתם, ושאותם אתם יכולים לבדוק כדי להרחיב את האופקים.
הסימון "O גדולה" (Big O) ומחקר סיבוכיות של אלגוריתמים זה משהו שהרבה מתכנתים בתעשייה ותלמידים מתחילים מוצאים כדבר שקשה להבנה, מפחדים ממנו או נמנעים ממנו לחלוטין תחת הטענה שהוא חסר תועלת. אבל הנושא הזה אינו קשה או תיאורטי כפי שהוא עלול להראות. סיבוכיות של אלגוריתמים היא רק דרך למדוד באופן רשמי כמה מהר התוכנית או האלגוריתם רצים, כך שמדובר במשהו מאוד תכליתי. בואו נתחיל במעט זריקת מוטיבציה לגבי הנושא.

מוטיבציה
אנחנו כבר יודעים שישנם כלים המודדים כמה מהר תוכנית רצה. ישנן תוכנות שנקראות Profilers המודדות את זמן ריצת התוכנית במילישניות ויכולות לעזור לנו לייעל את הקוד שלנו בעזרת זיהוי צווארי־בקבוק. זה אמנם כלי שימושי, אולם הוא לא באמת שייך להגדרת הסיבוכיות של האלגוריתם. הסיבוכיות של האלגוריתם היא משהו שעוצב על־מנת להשוות שני אלגוריתמים באותה רמה רעיונית – תוך התעלמות מפרטים קטנים כמו שפת התכנות שבה המימוש המסוים כתוב, החומרה עליה רץ האלגוריתם או קבוצת ההוראות האפשריות של המעבד הנתון. אנחנו רוצים להשוות אלגוריתמים כשאנחנו מתייחסים אך ורק למה שהם עצמם: רעיונות של איך משהו יחושב. לספור מילישניות לא יעזור לנו כאן. זה אפשרי למדי שאלגוריתם גרוע שממומש בשפת תכנות Low Level ("נמוכה") כמו אסמבלי ירוץ מהר יותר מאשר אלגוריתם טוב שכתוב בשפה עילית, כמו Python או Ruby. זה הזמן להגדיר מה זה אלגוריתם "טוב יותר".
כשמתייחסים לאלגוריתמים כתוכנות שמבצעות חישובים בלבד, ולא דברים אחרים כמו פעולות הקשורות ברשת או בקלט ופלט מהמשתמש, ניתוח הסיבוכיות מאפשר לנו למדוד כמה מהירה תוכנית כשהיא מבצעת חישובים. דוגמה לפעולות שהן חישוביות בלבד כוללות פעולות על מספרי נקודה צפה כמו חיבור וכפל; חיפוש אחר ערך מסוים בתוך מסד־נתונים שנכנס ב־RAM; מציאת נתיב שדמות עם בינה־מלאכותית תלך בו במשחק מחשב, כך שהיא תצטרך ללכת את המרחק הקטן ביותר בעולם הווירטואלי שסביבה (ראו איור 1); או הרצת בדיקת התאמה של תבנית ביטוי רגולרי על מחרוזת מסוימת. ללא ספק, חישוביות נמצאת בכל מקום במדעי המחשב.
ניתוח סיבוכיות הוא גם כלי שמאפשר לנו להסביר איך אלגוריתם מתנהג כשגודל הקלט שלנו עולה. אם נזין לאלגוריתם קלט שונה, איך הוא יתנהג? אם לאלגוריתם שלנו לוקח שנייה לרוץ על קלט בגודל 1000, איך הוא יתנהג אם אכפיל את גודל הקלט? האם הוא ירוץ בדיוק באותה מהירות, בחצי מהירות או במהירות שהיא פי ארבע איטית יותר? זה חשוב בתכנות מעשי, שכן זה מאפשר לנו לחזות איך האלגוריתם שלנו יתנהג כשכמות המידע שבקלט תגדל. לדוגמה, אם כתבנו אלגוריתם לתוכנת אינטרנט שעובד היטב עם 1000 משתמשים, ומדדנו את זמן הריצה שלו, בעזרת ניתוח סיבוכיות יהיה לנו מושג די טוב לגבי מה יקרה כשיהיה לנו 2000 משתמשים במקום. לצורך תחרויות אלגוריתמים, ניתוח סיבוכיות מספק לנו תובנות על הזמן שייקח לקוד שלנו לרוץ עבור אוסף הבדיקות הגדול ביותר בו ישתמשו כדי לבחון את נכונות התוכנית שלנו. אז אם מדדנו את התנהגות התוכנית שלנו עבור קלט קטן, נוכל לקבל מושג די טוב לגבי איך הוא יתנהג עבור קלטים גדולים יותר. בואו נתחיל בדוגמה פשוטה: מציאת האיבר הגדול ביותר במערך.
ספירת הוראות
במאמר הזה, אני הולך להשתמש בשפות תכנות שונות עבור הדוגמאות. עם זאת, אל חשש אם אתם לא מכירים שפת תכנות מסוימת. מכיוון שאתם יודעים לתכנת, אתם אמורים להיות מסוגלים לקרוא את הדוגמאות בלי שום בעיה אפילו אם אתם לא מכירים את שפת התכנות שנבחרה, שכן הן פשוטות ומכיוון שאני לא אשתמש באף יכולת אזוטרית של השפה. אם אתם תלמידים שמתחרים בתחרויות אלגוריתמים, אתם ככל הנראה עובדים עם C++, ולכן תוכלו לעקוב ללא בעיה. במקרה הזה אני ממליץ לעבוד על התרגילים ב־C++ לצורכי תרגול.
ניתן לחפש את האיבר הגדול ביותר במערך באמצעות קטע קוד פשוט, כמו קטע הקוד הזה, הכתוב ב־Javascript בהינתן כקלט מערך A בגודל n:
var M = A[ 0 ];
for ( var i = 0; i < n; ++i ) {
if ( A[ i ] >= M ) {
M = A[ i ];
}
}
עכשיו, הדבר הראשון שנעשה הוא לספור כמה הוראות בסיסיות קטע הקוד הזה מבצע. אנחנו נעשה את זה רק הפעם, וזה לא יהיה הכרחי בהמשך המאמר ובזמן פיתוח התיאוריה שלנו, אז תהיו סבלניים איתי עוד כמה רגעים בזמן שאנחנו עושים את זה. כשאנחנו מנתחים קטע קוד, אנחנו רוצים לשבור אותו להוראות פשוטות; דברים שיכולים להיות מורצים על ידי המעבד ישירות – או קרוב לזה. אנחנו נניח שהמעבד שלנו יכול לבצע כל אחת מהפעולות הבאות כהוראה אחת:
- הכנסת ערך למשתנה
- אחזור הערך במקום מסוים במערך
- השוואת שני ערכים
- קידום ערך
- פעולות אריתמטיות בסיסיות כמו חיבור או כפל
אנחנו נניח שסיעוף (הבחירה בין if ל־else בקוד אחרי שהתנאי שבתוך ה־if חושב) קורה מיד ולא נחשב כאחת מההוראות האלו. בקוד שלמעלה, השורה הראשונה היא:
var M = A[ 0 ];
זה מצריך 2 הוראות: אחת כדי למצוא את הערך של A[ 0 ] ואחת כדי להכניס את הערך ל־M (אנחנו מניחים ש־n, גודל המערך, הוא תמיד 1 לפחות). שתי ההוראות האלו תמיד מתבצעות, בלי קשר למה הערך של n. האתחול של לולאת ה־for גם חייב תמיד להתבצע. האתחול מייצר לנו עוד שתי הוראות; השמה והשוואה:
i = 0;
i < n;
הוראות אלו ירוצו לפני שלולאת ה־for תתחיל בחִזְרוּר (איטרציה; מופע) הראשון שלה. לאחר כל חזרור, אנחנו צריכים עוד שתי הוראות שירוצו, הגדלה של i והשוואה שמטרתה לבדוק האם אנחנו צריכים להישאר בלולאה:
++i;
i < n;
אז, אם נתעלם מגוף הלולאה, מספר ההוראות שהאלגוריתם צריך לבצע הוא 4 + 2n. המספר הזה הוא תוצאה של 4 הוראות בתחילת לולאת ה־for, ועוד 2 הוראות בסוף כל חזרור, כשסך החזרורים שלנו הוא n. כעת אנחנו יכולים להגדיר את הפונקציה המתמטית f( n ), אשר בהינתן n, נותנת לנו את מספר ההוראות שהאלגוריתם צריך להריץ. עבור לולאת for בלי גוף, יוצא לנו f( n ) = 4 + 2n.
ניתוח המקרה הגרוע ביותר
עכשיו, כשאנחנו מסתכלים על הגוף של לולאת ה־for, יש לנו פעולות שמתרחשות תמיד – פעולת אחזור מהמערך והשוואה:
if ( A[ i ] >= M ) { ...
אלו שתי הוראות. אבל הגוף של ה־if יכול לרוץ או לא לרוץ, בתלות במה הם הערכים שנמצאים במערך. אם יוצא ש־A[ i ] >= M, אנחנו נריץ שתי הוראות נוספות – אחזור ערך ממערך והשמה:
M = A[ i ]
אבל עכשיו אנחנו לא יכולים להגדיר את f( n ) בקלות שכזו, מכיוון שמספר ההוראות שלנו לא תלוי אך ורק ב־n, אלא גם בקלט עצמו. לדוגמה, עבור A = [ 1, 2, 3, 4 ] האלגוריתם יצטרך לבצע יותר פעולות מאשר עבור A = [ 4, 3, 2, 1 ]. כשמנתחים אלגוריתמים, אנחנו לעתים קרובות מחשבים את המצב הגרוע ביותר. מה הדבר הכי גרוע שיכול לקרות לאלגוריתם שלנו? מתי האלגוריתם יצטרך לבצע הכי הרבה פעולות כדי להשלים את הריצה שלו? עבור הקוד שכתבנו, מדובר במצב בו המערך מסודר בסדר עולה, כמו A = [ 1, 2, 3, 4 ]. במקרה הזה, האלגוריתם יחליף את M עם כל מעבר על תא במערך, ויצור את כמות ההוראות המרבית. לאנשי מדעי המחשב יש שם מגונדר לעניין, והם קוראים לזה "ניתוח המצב הגרוע ביותר"; שזה פשוט למצוא את המצב שבו יש לנו הכי פחות מזל. אז, במצב הגרוע ביותר, יש לנו 4 הוראות שאנחנו צריכים להריץ בגוף לולאת ה־for, ולכן f( n ) = 4 + 2n + 4n = 6n + 4. הפונקציה f, בהינתן גודל n, נותנת לנו את מספר ההוראות שאנחנו צריכים להריץ במקרה הגרוע ביותר.
התנהגות אסימפטוטית
בהינתן פונקציה שכזו, יש לנו מושג די טוב כמה מהיר האלגוריתם שלנו. למרות זאת, כמו שהבטחתי, אנחנו לא נצטרך לעשות משימות מייגעות של ספירת הוראות בתוכנית שלנו. חוץ מזה, מספר ההוראות שהמעבד שלנו מבצע עבור כל שפת תכנות תלוי בקומפיילר של שפת התכנות שלנו ובכמות ההוראות הקיימות במעבד (לדוגמה, בתלות האם המעבד שלכם הוא AMD או Intel Pentium במחשב שלכם, או מעבד MIPS בפלסטיישן 2) ואמרנו שאנחנו נתעלם מזה. עכשיו אנחנו נריץ את הפונקציה f דרך "מסנן" שיעזור לנו להיפטר מהפרטים הקטנים שאנשי מדעי־המחשב מעדיפים להתעלם מהם.
בפונקציה שלנו, 6n + 4, יש לנו 2 ביטויים. 6n ו־4. בניתוח סיבוכיות אכפת לנו רק מה קורה לפונקציית ספירת ההוראות כאשר הקלט של התוכנית (n) גדל. זה מתיישב עם רעיונות קודמים של התנהגות "המצב הגרוע־ביותר": השאלה שמעניינת אותנו היא איך האלגוריתם שלנו יתנהג כשמתייחסים אליו רע; כשהוא מאותגר עם ביצוע דבר קשה. שימו לב שזה ממש מועיל כשמשווים אלגוריתמים. אם אלגוריתם מנצח אלגוריתם אחר בהינתן קלט גדול, ככל הנראה האלגוריתם המהיר יותר יישאר מהיר יותר כשיתנו לו קלט פשוט יותר או קטן יותר. מתוך האיברים שיצאו לנו ב־f, אנחנו נשמיט את כל האיברים שגדלים לאט, ונשמור רק את האיברים שגדלים הכי מהר כש־n גדל. 4 בבירור נשאר 4 כש־n גדל, אבל 6n גדל וגדל, אז הוא נוטה להיות חשוב יותר ויותר עבור בעיות גדולות יותר. לכן, הדבר הראשון שנעשה זה להשמיט את 4 ולהשאיר את הפונקציה בצורה f( n ) = 6n.
זה הגיוני כשאתם חושבים על זה, שכן 4 הוא סך הכול "קבוע אתחול". לשפות תכנות שונות יכול לקחת זמן שונה לאתחל דברים. לדוגמה, ל־Java לוקח הרבה זמן לאתחל את המכונה הווירטואלית שלה. מכיוון שאנחנו מתעלמים מההבדל בין שפות תכנות שונות, זה הגיוני מאוד להתעלם מהערך הזה.
הדבר השני שנתעלם ממנו הוא מקדם ההכפלה שנמצא לפני n, ולכן הפונקציה שלנו תהפוך להיות f( n ) = n. כפי שאתם יכולים לראות, זה מפשט דברים מאוד. שוב, יש היגיון מסוים בלהשמיט את מקדם ההכפלה אם אנחנו חושבים על איך שפות תכנות שונות עוברות הִדּוּר (קומפילציה). הפעולה של "אחזור מהמערך" יכולה לעבור הידור למספר שונה של הוראות בשפות תכנות שונות. לדוגמה, ב־C, הפעולה A[ i ] לא כוללת בדיקה ש־i נמצא בגבולות המוצהרים של המערך, בזמן שב־Pascal היא כן. אז, הקוד הבא שכתוב ב־Pascal:
M := A[ i ]
שווה ערך לקוד הבא שכתוב ב־C:
if ( i >= 0 && i < n ) {
M = A[ i ];
}
אז זה סביר לצפות ששפות תכנות שונות יניבו מקדמי הכפלה שונים כשאנחנו סופרים את ההוראות שלהם. בדוגמה שלנו בה אנחנו משתמשים במהדר טיפש עבור Pascal שאינו מודע לצורות מִטּוּב אפשריות, Pascal תצריך ביצוע של 3 הוראות עבור כל גישה למערך במקום הוראה אחת בה יהיה צורך ב־C. השמטת מקדם ההכפלה הולכת בד־בבד עם הרעיון של התעלמות משפות־תכנות וממהדרים מסוימים, וניתוח הרעיון של האלגוריתם עצמו בלבד.
המסננת הזו של "להשמיט את כל מקדמי ההכפלה" ו"להשאיר את האיבר שגדל במהירות הגבוהה ביותר" כפי שתואר למעלה יוצרת לנו את הדבר שנקרא התנהגות אסימפטוטית. אז ההתנהגות האסימפטוטית של f( n ) = 2n + 8 מתוארת על ידי הפונקציה f( n ) = n. מבחינה מתמטית, מה שאנחנו אומרים כאן זה שאנחנו מעוניינים בגבול של הפונקציה f כש־n שואף לאינסוף; אבל אם אתם לא יודעים מה הביטוי הזה אומר באופן רשמי, אל דאגה, מה שלמדתם זה כל מה שאתם צריכים לדעת. (כהערת צד, בסביבה מתמטית קפדנית, לא נוכל להשמיט את הקבועים בגבול; אבל למטרות המדעי־המחשב, אנחנו רוצים לעשות את זה מהסיבות שפורטו למעלה). בואו נעבוד על כמה דוגמאות כדי להכיר לעצמנו את הרעיון.
נמצא את ההתנהגות האסימפטוטית של הדוגמאות הבאות בעזרת השמטה של מקדמי ההכפלה, ושמירה על האיברים שגדלים הכי מהר.
f( n ) = 5n + 12 נותן לנו f( n ) = n.
על־ידי שימוש בהנמקות שכתובות למעלה.
f( n ) = 109 נותן לנו f( n ) = 1.
אנחנו משמיטים את הכופל 109 * 1, אבל אנחנו עדיין צריכים לשים כאן 1 על־מנת לציין שלפונקציה הזו יש ערך שאינו 0.
f( n ) = n2 + 3n + 112 נותן לנו f( n ) = n2
במקרה הזה, n2 גדל מהר יותר מ־3n עבור כל n גדול מספיק, אז אנחנו נשמור אותו.
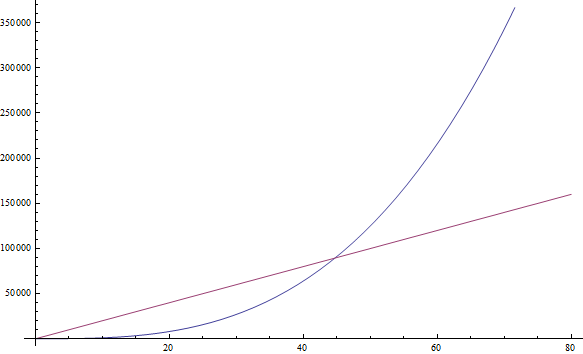
f( n ) = n3 + 1999n + 1337 נותן לנו f( n ) = n3
אפילו שהמכפיל לפני n הוא די גדול, אנחנו עדיין יכולים למצוא n גדול מספיק כך ש־n3 יהיה גדול מ־1999n. מכיוון שאנחנו מתעניינים בהתנהגות עבור ערכים גדולים מאוד של n, אנחנו נשמור רק את n3 (ראו איור 2).
f( n ) = n +
 נותן לנו f( n ) = n
נותן לנו f( n ) = nמכיוון ש־n גדל מהר יותר מאשר
 ככל שאנחנו מגדילים את n.
ככל שאנחנו מגדילים את n.
אתם יכולים לנסות את הדוגמאות הבאות בעצמכם:
תרגיל 1
- f( n ) = n6 + 3n
- f( n ) = 2n + 12
- f( n ) = 3n + 2n
- f( n ) = nn + n
(כתבו לעצמכם את התוצאות; הפתרונים מופיעים למטה).
אם אתם מסתבכים עם אחת מהדוגמאות למעלה, הכניסו מספר גדול ל־n ובדקו איזה מהאיברים גדול יותר. די פשוט, הא?
סיבוכיות
מסתמן שמכיוון שאנחנו יכולים להשמיט את כל המקדמים שמקשטים לנו את הפונקציה, די קל להגיד מה היא ההתנהגות האסימפטוטית של פונקציה שסופרת את כמות ההוראות בתוכנית. למעשה, בכל תוכנית שבה אין שום סוג של לולאות – ההתנהגות האסימפטוטית תהיה f( n ) = 1, מאחר שמספר ההוראות שהיא צריכה לבצע הוא פשוט קבוע (אלא אם היא משתמשת ברקורסיה; ראו מטה). ההתנהגות האסימפטוטית של כל תוכנית עם לולאה בודדת שרצה מ־1 ועד n תהיה f( n ) = n, מכיוון שהיא תעשה כמות קבועה של הוראות לפני הלולאה, כמות קבועה של הוראות אחרי הלולאה וכמות קבועה של הוראות בתוך הלולאה, שכולן ירוצו n פעמים.
זה אמור להיות קל הרבה יותר ופחות מעייף מאשר לספור הוראות אחת־אחת, אז בואו ונציץ בכמה דוגמאות כדי להכיר את הרעיון. התוכנית הבאה ב־PHP בודקת האם ערך מסוים קיים בתוך מערך A בגודל n.
<?php
$exists = false;
for ( $i = 0; $i < n; ++$i ) {
if ( $A[ $i ] == $value ) {
$exists = true;
break;
}
}
?>
השיטה הזו של חיפוש בתוך מערך נקראת חיפוש לינארי. זה שם סביר, מכיוון שההתנהגות האסימפטוטית של התוכנית היא f( n ) = n (אנחנו נגדיר בדיוק מה "לינארי" אומר בחלק הבא). יתכן ששמתם לב לפקודה “break” שמופיעה כאן, שעלולה לסיים את ריצתה של התוכנית מוקדם יותר, אפילו אחרי חזרור אחד בלבד. אך זכרו שאנחנו מעוניינים במצב הגרוע ביותר, שעבור התוכנית הזו הוא שמערך A לא כולל את הערך. אז ההתנהגות האסימפטוטית היא עדיין f( n ) = n.
תרגיל 2
נתחו את מספר ההוראות בתוכנית PHP שלמעלה ביחס ל־n במקרה הגרוע ביותר, על מנת למצוא את f( n ), בדומה לצורה בה ניתחנו את תוכנית ה־JavaScript. לאחר מכן ודאו שמבחינת התנהגות אסימפטוטית, התוכנית שלנו אכן עונה ל־f( n ) = n.
בואו נביט בתוכנית Python שמחברת שני איברים של מערכים אחד לשני, על־מנת לייצר סכום שמאוחסן במשתנה אחר:
v = a[ 0 ] + a[ 1 ]
כאן יש לנו מספר קבוע של הוראות, כך ש־f( n ) = 1.
תוכנית ה־C++ הבאה בודקת האם וקטור (מערך משוכלל) בשם A ובגודל n מכיל שני ערכים זהים בתוכו:
bool duplicate = false;
for ( int i = 0; i < n; ++i ) {
for ( int j = 0; j < n; ++j ) {
if ( i != j && A[ i ] == A[ j ] ) {
duplicate = true;
break;
}
}
if ( duplicate ) {
break;
}
}
מכיוון שיש לנו כאן שתי לולאות המקוננות אחת בתוך השנייה, ההתנהגות האסימפטוטית של האלגוריתם תתואר כ־f( n ) = n2.
כלל אצבע: ניתן לנתח תוכניות פשוטות על־ידי ספירת הלולאות המקוננות. לולאה בודדת מייצרת f( n ) = n. לולאה בתוך לולאה מייצרת f( n ) = n2. לולאה בתוך לולאה בתוך לולאה מייצרת f( n ) = n3.
אם יש לנו תוכנית שקוראת לפונקציה מתוך לולאה, ואנחנו יודעים את מספר ההוראות שהפונקציה מבצעת, קל יהיה להחליט מה מספר ההוראות שהתוכנית כולה הולכת לבצע. ניקח את תוכנית ה־C הבאה כדוגמה:
int i;
for ( i = 0; i < n; ++i ) {
f( n );
}
אם אנחנו יודעים ש־f( n ) היא פונקציה שמבצעת בדיוק n הוראות, אז אנחנו יודעים שמספר ההוראות של כל התוכנית הוא אסימפטוטית n2, שכן הפונקציה נקראת בדיוק n פעמים.
כלל אצבע: בהינתן מספר לולאות נפרדות, האיטית שבהן תכריע את ההתנהגות האסימפטוטית של התוכנית. ההתנהגות האסימפטוטית של תוכנית בעלת שתי לולאות מקוננות שאחריהן יש לולאה בודדת, זהה להתנהגות האסימפטוטית של תוכנית בעלת שתי לולאות מקוננות. זאת משום שהלולאות המקוננות חוֹלְשׁוֹת על הלולאה הבודדת.
עכשיו, בואו נתחיל להשתמש בסימונים המגונדרים שבהם משתמשים אנשי מדעי־המחשב. אחרי שנבין בדיוק את ההתנהגות האסימפטוטית של התוכנית ונסמן אותה ב־f, נוכל להגיד על התוכנית שלנו שהיא Θ( f( n ) ). לדוגמה, התוכנות שהצגנו למעלה הן Θ( 1 ), Θ( n2 ) ו־Θ( n2 ) בהתאמה. את Θ( n ) אנחנו מבטאים כ"תטא של n". לפעמים אנחנו אומרים ש־f( n ), הפונקציה המקורית שבה ספרנו את ההוראות כולל הקבועים, היא Θ ( משהו ). לדוגמה, אנחנו יכולים להגיד ש־f( n ) = 2n היא פונקציה שהיא Θ( n ) – שום דבר חדש עד כאן. אנחנו גם יכולים לכתוב 2n ∈ Θ( n ), שמבוטא כ"שתי n הוא תטא של n". אל תתבלבלו בגלל הסימונים: כל מה שהם אומרים זה שאם ספרנו את מספר ההוראות בתוכנית ויצא לנו 2n, אז ההתנהגות האסימפטוטית של האלגוריתם שלנו מתוארת כ־n, ואותה מצאנו על־ידי השמטת המקדמים. בהינתן הסימון הזה, הטענות הבאות הן נכונות מתמטית:
- n6 + 3n ∈ Θ( n6 )
- 2n + 12 ∈ Θ( 2n )
- 3n + 2n ∈ Θ( 3n )
- nn + n ∈ Θ( nn )
דרך אגב, אם פתרתם את תרגיל 1 שהופיע מעלה, אלו הן בדיוק התשובות שהייתם צריכים לקבל.
אנחנו קוראים לפונקציה הזו, למה שאנחנו שמים ב־Θ ( כאן ), סיבוכיות הזמן או פשוט הסיבוכיות של האלגוריתם שלנו. אז על אלגוריתם שהוא Θ( n ) אפשר להגיד שהוא מסיבוכיות n. יש לנו גם שמות מיוחדים עבור המקרים Θ( 1 ), Θ( n ), Θ( n2 ) ועבור Θ( log( n ) ) מכיוון שהם נפוצים מאוד. אנחנו אומרים שאלגוריתם שמוגדר כ־Θ( 1 ) הוא בעל זמן ריצה קבוע, Θ( n ) הוא לינארי, Θ( n2 ) הוא ריבועי ו־ Θ( log( n ) ) הוא לוגריתמי (אל תדאגו אם אתם לא יודעים מה זה לוגריתמים עדיין – אנחנו נגיע לזה עוד דקה).
כלל אצבע: תוכניות שיש להן ערך Θ גדול יותר רצות לאט יותר מאשר תוכניות עם ערך Θ קטן יותר.

סימון O גדולה (Big-O)
עכשיו, זה נכון שלפעמים קשה להבין מה ההתנהגות המדויקת של אלגוריתם בצורה שביצענו למעלה, במיוחד עבור דוגמאות מורכבות יותר. עם זאת, נוכל להגיד שההתנהגות של האלגוריתם שלנו לעולם לא תחצה חסם מסוים. זה יהפוך את החיים שלנו להרבה יותר קלים, משום שאנחנו לא נצטרך לציין בדיוק כמה מהר האלגוריתם שלנו רץ, אפילו כשמתעלמים מקבועים בצורה שעשינו לפני־כן. כל מה שנצטרך לעשות עכשיו הוא למצוא את החסם המסוים. אפשר להסביר את זה בקלות על־ידי דוגמה.
בעיה מפורסמת שאנשי מדעי־המחשב משתמשים בה כדי ללמד אלגוריתמים היא בעיית המיון. בבעיית המיון, נתון מערך A מגודל n (נשמע מוכר?) ואנחנו מתבקשים לכתוב תוכנית שתמיין אותו לפי הסדר. הבעיה הזו מעניינת מכיוון שהיא בעיה מעשית שקיימת במערכות אמיתיות. לדוגמה, מערכת קבצים צריכה למיין את הקבצים שהיא מציגה לפי שם כך שהמשתמש יוכל להתמצא בהם בקלות. או, דוגמה אחרת, משחק מחשב עשוי להיות צריך למיין חפצים תלת־ממדיים המוצגים בעולם לפי המרחק שלהם מעיניו של השחקן בעולם הווירטואלי כדי להחליט מה נראה ומה לא, דבר שלפעמים נקרא בעיית הנראות (ראו איור 3). החפצים שמתברר שהם הקרובים ביותר לשחקן הופכים לנראים, בעוד אלו הרחוקים ממנו אולי מוחבאים על־ידי חפצים אחרים שנמצאים לפניהם. מיון גם מעניין מכיוון שיש הרבה אלגוריתמים שפותרים אותו, וחלק מהם פחות טובים מאחרים. זו גם בעיה שקל להסביר ולהגדיר אותה. אז בואו נכתוב קוד שממיין מערך.
הנה דרך לא יעילה למימוש של מיון מערך ב־Ruby. (כמובן, Ruby תומכת בסידור מערכים בעזרת פונקציות מובנות שבהן כדאי להשתמש במקום, ושבטוח מהירות יותר ממה שאנחנו נראה כאן. אבל הדוגמה הזו כאן למטרות המחשה).
b = []
n.times do
m = a[ 0 ]
mi = 0
a.each_with_index do |element, i|
if element < m
m = element
mi = i
end
end
a.delete_at( mi )
b << m
end
שיטה זו נקראת מיון בחירה. היא מוצאת את המספר הנמוך ביותר במערך שלנו (המערך שהוזכר למעלה. הערך המינימלי מסומן ב־m ו־mi הוא המיקום שלו במערך), שמה אותו בסוף מערך חדש (במקרה שלנו b) ומסירה אותו מהמערך המקורי. בשלב הזה היא מוצאת את הערך הקטן מבין הערכים שנשארו במערך המקורי שלנו, ומוסיפה אותו למערך החדש שלנו שעכשיו כולל שני איברים, ומוחקת אותו מהמערך המקורי. היא ממשיכה בתהליך הזה עד שכל האיברים נמחקו מהמערך המקורי וסודרו. בדוגמה הזו, כפי שאתם יכולים לראות, יש לנו שתי לולאות מקוננות. הלולאה החיצונית רצה n פעמים, והפנימית רצה פעם אחת עבור כל איבר במערך a. בזמן שבמערך a היו בהתחלה n איברים, מחקנו איבר אחד בכל חזרור. אז הלולאה הפנימית חוזרת על עצמה n פעמים במהלך החזרור הראשון של הלולאה החיצונית, ואז n - 1 פעמים, ואז n – 2 פעמים וכן הלאה, עד החזרור האחרון של הלולאה החיצונית שבו היא רצה רק פעם אחת.
קצת קשה להעריך את הסיבוכיות של התוכנית הזו, שכן אנחנו צריכים להבין מה הסכום של 1 + 2 + … + (n – 1) + n. אבל אנחנו בוודאות יכולים להגיד מה "החסם העליון" של הסיבוכיות. הכוונה היא שאנחנו יכולים לשנות את התוכנית (אתם יכולים לעשות את זה בראש, לא בקוד המקורי) כדי להפוך אותה לגרועה יותר ממה שהיא ואז למצוא את הסיבוכיות של התוכנית החדשה שיצרנו. אם אנחנו יכולים למצוא את הסיבוכיות של התוכנית הגרועה יותר שבנינו, אנחנו יודעים שהתוכנית המקורית שלנו לא תהיה יותר גרועה ממנה, וייתכן שתהיה אפילו טובה יותר. בצורה הזו, אם אנחנו נמצא שהתוכנית הערוכה שלנו כתובה בסיבוכיות די טובה, שגרועה מהסיבוכיות של התוכנית המקורית, אנחנו נוכל להסיק שגם לתוכנית המקורית שלנו יש סיבוכיות טובה למדי – טובה לפחות כמו התוכנית הערוכה, או אולי אפילו טובה יותר.
בואו נחשוב עכשיו על דרך לערוך את תוכנת הדוגמה כדי שיהיה פשוט יותר להעריך את הסיבוכיות שלה. אבל בואו נזכור שאנחנו יכולים לעשות את זה רק על־ידי הפיכתה לגרועה יותר, משמע, יותר הוראות, כך שהשערוך שלנו יהיה בעל משמעות עבור התוכנית המקורית. די ברור שאנחנו יכולים לשנות את הלולאה הפנימית של התוכנית כך שתתבצע תמיד n פעמים במקום מספר משתנה של פעמים. חלק מהחזרות האלו לא יהיו מועילות, אבל זה יעזור לנו לנתח את הסיבוכיות של האלגוריתם שייווצר. אם אנחנו עושים את השינוי הזה, האלגוריתם החדש שבנינו הוא בבירור Θ( n2 ), מכיוון שיש לנו שתי לולאות מקוננות, כאשר כל אחת מהן מתבצעת בדיוק n פעמים. אם זה המצב, אנחנו אומרים שהאלגוריתם המקורי הוא O( n2 ). O( n2 ) מבוטא כ"או גדולה של n בריבוע". מה שזה אומר זה שהתוכנית שלנו מבחינה אסימפטוטית לא גרועה יותר מ־n2. היעילות שלה עשויה להיות טובה יותר, או בדיוק כזו. דרך אגב, אם התוכנית שלנו היא באמת Θ( n2 ), אנחנו עדיין יכולים להגיד שהיא O( n2 ). כדי לעזור לכם להבין את זה, דמיינו שאתם משנים את התוכנית המקורית ככה שהיא לא משתנה הרבה, אבל עדיין נהיית מעט גרועה יותר; נניח בעזרת הוספת כמה הוראות חסרות משמעות בתחילת התוכנית. אם תעשו את זה אתם תשנו את הפונקציה של ספירת ההוראות בקבוע מסוים, שממנו נתעלם כשנבדוק מה ההתנהגות האסימפטוטית של התוכנית. אז התוכנית הזו, שהיא Θ( n2 ), היא גם O( n2 ).
אבל תוכנית שהיא O( n2 ) עלולה לא להיות Θ( n2 ). לדוגמה, כל תוכנית שהיא Θ( n ) היא גם O( n2 ) למרות שהיא גם O( n ). אם אנחנו מדמיינים שתוכנית המתוארת באמצעות Θ( n ) היא למעשה לולאה פשוטה שחוזרת על עצמה n פעמים, אנחנו יכולים לגרום לה להיות גרועה יותר אם נעטוף אותה בלולאה נוספת שגם היא חוזרת על עצמה n פעמים, ובכך לייצר תוכנית שבה f( n ) = n2. בכלליות, כל תוכנית Θ( a ) היא גם O( b ) כאשר b גרוע מ־a. שימו לב שהשינוי לתוכנית לא צריך להיות בעל משמעות או זהה לחלוטין לתוכנית הקודמת. הוא רק צריך לבצע יותר פעולות מאשר התוכנית המקורית עבור n נתון. כל מה שאנחנו עושים זה לספור הוראות, לא באמת לפתור את הבעיה שלנו.
אז, בעצם זה שאנחנו אומרים שהתוכנית שלנו היא O( n2 ) אנחנו הולכים על בטוח: ניתחנו את האלגוריתם שלנו ומצאנו שהוא לעולם לא יותר גרוע מ־n2. אבל יכול להיות שהוא למעשה n2. זה נותן לנו הערכה טובה לכמה מהר התוכנית שלנו רצה. בואו נעשה כמה דוגמאות כדי לעזור לכם להכיר את הסימון החדש הזה.
תרגיל 3
מצא איזה מהבאים הוא נכון:
- אלגוריתם שהוא Θ( n ) הוא גם O( n )
- אלגוריתם שהוא Θ( n ) הוא גם O( n2 )
- אלגוריתם שהוא Θ( n2 ) הוא גם O( n3 )
- אלגוריתם שהוא Θ( n ) הוא גם O( 1 )
- אלגוריתם שהוא O( 1 ) הוא גם Θ( 1 )
- אלגוריתם שהוא O( n ) הוא גם Θ( 1 )
פתרון
- אנחנו יודעים שזה נכון משום שאם התוכנית המקורית הייתה Θ( n ) אנחנו יכולים להשיג O( n ) בלי לערוך את התוכנית.
- מכיוון ש־n2 הוא גרוע מ־n, זה נכון.
- מכיוון ש־n3 הוא גרוע מ־n2, זה נכון.
- מכיוון ש־1 הוא לא גרוע מ־n, זה לא נכון. אם התנהגות אסימפטוטית של התוכנית היא n (מספר לינארי של הוראות), אנחנו לא יכולים להפוך אותה לגרועה יותר בכך שההתנהגות האסימפטוטית שלה תהיה הוראה אחת (מספר קבוע של הוראות).
- זה נכון מכיוון ששתי הערכות הסיבוכיות זהות.
- זה יכול להיות נכון או לא, בתלות באלגוריתם. במקרה הכללי זה לא נכון. אם ישנו אלגוריתם שאנחנו יודעים שהוא Θ( 1 ), אז הוא בוודאות O( n ). אבל אם הוא O( n ) הוא יכול לא להיות Θ( 1 ). לדוגמה, אלגוריתם שהוא Θ( n ) הוא O( n ) אבל לא Θ( 1 ).
תרגיל 4
השתמשו בסכום סידרה חשבונית כדי להוכיח שהתוכנית שהוצגה למעלה היא לא רק O( n2 ), אלא גם Θ( n2 ). אם אתם לא יודעים איך מחשבים סכום של סדרה חשבונית, קראו על הנושא בוויקיפדיה – זה קל.
מכיוון שסיבוכיות O גדולה של אלגוריתמים מבטאת את החסם העליון של סיבוכיות האלגוריתם, בעוד ש־Θ מבטאת את הסיבוכיות האמיתית של האלגוריתם, אנחנו לפעמים אומרים ש־Θ נותנת לנו חסם הדוק. אם אנחנו יודעים שמצאנו חסם שאינו הדוק, אנחנו יכולים להשתמש באות o קטנה כדי לסמן את זה. לדוגמה, אם אלגוריתם הוא Θ( n ), אז החסם ההדוק של הסיבוכיות שלו הוא n. לכן האלגוריתם הוא גם O( n ) וגם O( n2 ). מכיוון שהאלגוריתם הוא Θ( n ), החסם O( n ) הוא החסם ההדוק. אבל החסם O( n2 ) אינו הדוק, ולכן אנחנו יכולים לרשום שהאלגוריתם הוא o( n2 ), קרי "o קטנה של n בריבוע" כדי לציין שאנחנו יודעים שהחסם שלנו אינו הדוק. טוב יותר למצוא חסמים הדוקים לאלגוריתמים שלנו, מכיוון שהם נותנים לנו יותר מידע על איך האלגוריתם שלנו מתנהג, אבל זה לא תמיד קל.
תרגיל 5
החליטו אילו מהחסמים הבאים הם חסמים הדוקים ואילו אינם חסמים הדוקים. בדקו אם חסמים מסוימים יכולים להיות שגויים. השתמשו בסימון o על מנת לציין את החסמים הלא הדוקים.
- אלגוריתם שהוא Θ( n ) עבורו מצאנו את החסם העליון O( n ).
- אלגוריתם שהוא Θ( n2 ) עבורו מצאנו את החסם העליון O( n3 ).
- אלגוריתם שהוא Θ( 1 ) עבורו מצאנו את החסם העליון O( n ).
- אלגוריתם שהוא Θ( n ) עבורו מצאנו את החסם העליון O( 1 ).
- אלגוריתם שהוא Θ( n ) עבורו מצאנו את החסם העליון O( 2n ).
פתרון
- במקרה הזה, הסיבוכיות Θ והסיבוכיות O הן אותו דבר, אז החסם הדוק.
- כאן אנחנו רואים שהסיבוכיות O גדולה בקנה מידה מאשר הסיבוכיות Θ, אז החסם אינו הדוק. החסם O( n2 ) אכן יהיה חסם הדוק. אז אנחנו יכולים לרשום שהאלגוריתם הוא o( n3 ).
- שוב אנחנו רואים שהסיבוכיות O גדולה בקנה מידה מהסיבוכיות Θ, אז החסם אינו הדוק. החסם O( 1 ) יהיה הדוק. אנחנו יכולים להגיד שהחסם O( n ) אינו הדוק אם נרשום אותו כ־o( n ).
- כנראה שעשינו טעות כשחישבנו את החסם, מכיוון שהוא מוטעה. זה לא הגיוני שהחסם העליון של אלגוריתם Θ( n ) יהיה O( 1 ), מכיוון שסיבוכיות n גדולה מסיבוכיות 1. זכרו ש־O מספק לנו את החסם העליון.
- זה עלול להראות כאילו החסם פה אינו חסם הדוק, אבל למעשה זה לא נכון. החסם פה הוא חסם הדוק. זכרו שמבחינת התנהגות אסימפטוטית, 2n ו־n זה אותו דבר. אז אנחנו יכולים להגיד ש־O( 2n ) = O( n ) ולכן החסם הזה הדוק, שכן הסיבוכיות הזו זהה ל־Θ.
כלל אצבע: קל יותר למצוא את סיבוכיות ה־O של אלגוריתם מאשר להבין את סיבוכיות ה־Θ שלו.
יתכן שאתם קצת בשוק מכל הסימונים החדשים האלו, אבל בואו נלמד על שניים נוספים לפני שאנחנו ממשיכים הלאה לכמה דוגמאות. הם יהיו פשוטים עכשיו כשאתם מכירים את Θ, O ו־o, ואנחנו לא נשתמש בהם הרבה בהמשך המאמר, אבל זה טוב להכיר אותם בנקודה הזו. בדוגמה למעלה, ערכנו את התוכנית שלנו כדי להפוך אותה לגרועה יותר (על־ידי זה שהיא צריכה לבצע יותר הוראות, ומכאן שלוקח לה יותר זמן) ויצרנו את הסימון O. הסימון O משמעותי מכיוון שהוא אומר לנו שהתוכנית שלנו לעולם לא תרוץ באופן איטי יותר מאשר חסם מסוים, ולכן היא נותנת לנו מידע ערכי שמאפשר לנו לטעון שהתוכנית שלנו טובה מספיק. אם נעשה את הדבר ההפוך ונערוך את התוכנית שלנו כך שתהיה טובה יותר ונמצא מה הסיבוכיות של התוכנית שיצאה, אנחנו נשתמש בסימן Ω. מכאן, ש־Ω נותן לנו סיבוכיות שאנחנו יודעים שהתוכנית שלנו לא תהיה טובה ממנה. זה שימושי כשאנחנו רוצים להוכיח שהתוכנית שלנו איטית, או שהאלגוריתם שלנו גרוע. ניתן להשתמש בשיטה זו כדי לטעון שהאלגוריתם הוא איטי מדי מכדי שיעבוד במקרה מסוים. לדוגמה, אם נגיד שאלגוריתם הוא Ω( n3 ), זה אומר שהאלגוריתם אינו טוב יותר מ־n3. יכול להיות שהוא Θ( n3 ), אולי הוא גרוע ברמה של Θ( n4 ) או אפילו גרוע יותר, אבל אנחנו יודעים שהוא גרוע לפחות במידה מסוימת. אז Ω נותן לנו חסם תחתון עבור הסיבוכיות של האלגוריתם שלנו. בצורה דומה ל־o, אנחנו יכולים לרשום ω אם אנחנו מאמינים שהחסם שלנו אינו הדוק. לדוגמה, אלגוריתם שהוא Θ( n3 ) הוא גם ο( n4 ) וגם ω( n2 ). את הסימון Ω( n ) מבטאים כ"אומגה גדולה של n", בזמן שאת הסימון ω( n ) מבטאים כ"אומגה קטנה של n".
תרגיל 6
עבור ביטויי סיבוכיות ה־Θ הבאים, כתבו חסמים הדוקים ולא הדוקים של O ושל Ω לבחירתכם, בהינתן שהם קיימים.
- Θ( 1 )
- Θ(
 )
) - Θ( n )
- Θ( n2 )
- Θ( n3 )
פתרון
מדובר ביישום ישיר של ההגדרות שהופיעו למעלה.
- החסמים ההדוקים הם O( 1 ) ו־Ω( 1 ). חסם לא הדוק של O יכול להיות O( n ). זכרו ש־O מספקת לנו חסם עליון. מכיוון ש־n גדול יותר בסדר גודל מאשר 1, זהו חסם שאינו הדוק ואנחנו יכולים לרשום אותו גם כ־o( n ), אבל אנחנו לא יכולים למצוא חסם לא הדוק עבור Ω, שכן אי אפשר לרדת מ־1 בפונקציות האלו. נאלץ להישאר עם החסם ההדוק.
- החסם ההדוק חייב להיות כמו הסיבוכיות של Θ, ולכן הוא נשאר O(
 ) ו־Ω(
) ו־Ω(  ) בהתאמה. עבור חסמים שאינם הדוקים נוכל לקחת את O( n ), שכן n גדול יותר מאשר
) בהתאמה. עבור חסמים שאינם הדוקים נוכל לקחת את O( n ), שכן n גדול יותר מאשר  ולכן הוא חסם עליון עבור
ולכן הוא חסם עליון עבור  . כפי שאנחנו יודעים זהו חסם עליון שאינו הדוק, ולכן אנחנו יכולים לכתוב אותו גם כ־o( n ). עבור חסם תחתון שאינו הדוק אנחנו יכולים להשתמש פשוט ב־Ω( 1 ). כפי שאנחנו יודעים החסם הזה אינו הדוק, ואנחנו יכולים גם לכתוב אותו כ־ω( 1 ).
. כפי שאנחנו יודעים זהו חסם עליון שאינו הדוק, ולכן אנחנו יכולים לכתוב אותו גם כ־o( n ). עבור חסם תחתון שאינו הדוק אנחנו יכולים להשתמש פשוט ב־Ω( 1 ). כפי שאנחנו יודעים החסם הזה אינו הדוק, ואנחנו יכולים גם לכתוב אותו כ־ω( 1 ). - החסמים ההדוקים הם O( n ) ו־Ω( n ). שני חסמים לא הדוקים יכולים להיות ω( 1 ) ו־o( n3 ). אלו חסמים די גרועים, מכיוון שהם מאוד רחוקים מהסיבוכיות המקורית, אבל הם עדיין תקינים לפי ההגדרות שלנו.
- החסמים ההדוקים הם O( n2 ) ו־Ω( n2 ). עבור חסמים שאינם הדוקים אנחנו יכולים להשתמש שוב ב־ω( 1 ) וב־o( n3 ), כמו בדוגמה הקודמת.
- החסמים ההדוקים הם O( n3 ) ו־Ω( n3 ) בהתאמה. שני חסמים לא הדוקים יכולים להיות ω(
 n2 ) ו־o(
n2 ) ו־o(  n3 ). למרות שהחסמים האלו אינם הדוקים, הם עדיין טובים יותר מהחסמים שנתנו למעלה.
n3 ). למרות שהחסמים האלו אינם הדוקים, הם עדיין טובים יותר מהחסמים שנתנו למעלה.
הסיבה שאנחנו משתמשים ב־O וב־Ω במקום ב־Θ למרות ש־O ו־Ω יכולות גם לתת לנו חסמים הדוקים היא שלפעמים אנחנו לא נהיה מסוגלים להגיד אם החסם שמצאנו הוא הדוק, או שייתכן שפשוט אנחנו לא רוצים לעבור את התהליך של לבחון את החסם לעומק.
אם אתם לא זוכרים את כל הסימונים והשימושים שלהם, אל תתנו לזה להטריד אתכם. אתם תמיד יכולים לחזור ולהסתכל. הסימונים החשובים ביותר הם O ו־Θ.
בנוסף, שימו לב שלמרות ש־Ω מספקת לנו חסם תחתון להתנהגות הפונקציה שלנו (שיפרנו את התוכנית וגרמנו לה לבצע פחות הוראות) אנחנו עדיין נתייחס ל"ניתוח המקרה הגרוע ביותר". זאת משום שאנחנו מזינים לתוכנית שלנו את הקלט הגרוע ביותר האפשרי עבור n נתון, ומנתחים את ההתנהגות שלה תחת ההנחה הזו.
הטבלה הבאה מציינת את הסימונים שהצגנו זה עתה ואת סימון השוויון המתמטי המתאים להם עבור שימוש במספרים. הסיבה בגינה אנחנו לא משתמשים בסימונים הרגילים כאן ומשתמשים באותיות יווניות במקום, היא על מנת לציין שאנחנו עושים השוואה של התנהגות אסימפטוטית, ולא השוואה פשוטה.
| אופרטור להשוואה בין אסימפטוטות | אופרטור להשוואה בין מספרים |
|---|---|
| האלגוריתם שלנו הוא o( משהו ) | מספר מסוים < ממשהו |
| האלגוריתם שלנו הוא O( משהו ) | מספר מסוים ≤ ממשהו |
| האלגוריתם שלנו הוא Θ( משהו ) | מספר מסוים = למשהו |
| האלגוריתם שלנו הוא Ω( משהו ) | מספר מסוים ≥ ממשהו |
| האלגוריתם שלנו הוא ω( משהו ) | מספר מסוים > ממשהו |
כלל אצבע: בזמן שכל הסימונים O, o, Ω, ω ו־Θ שימושיים מדי פעם, הסימון O הוא הנפוץ ביותר, שכן יותר קל להכריע את ערכו מאשר את ערכו של Θ והוא יותר שימושי למטרות מעשיות מאשר Ω.
לוגריתמים
אם אתם יודעים מה זה לוגריתמים, תרגישו בנוח לדלג מעל היחידה הזו. מכיוון שהרבה אנשים לא מכירים את הרעיון של לוגריתמים, או אפילו לא השתמשו בהם לאחרונה ולא זוכרים אותם, היחידה הזו כאן כמבוא עבורם. המלל הזה הוא גם עבור תלמידים צעירים שעדיין לא ראו לוגריתמים בבית־הספר. לוגריתמים חשובים מכיוון שהם מופיעים הרבה כשמנתחים סיבוכיות. לוגריתם היא פעולה שמוחלת על מספר והופכת אותו לקטן יותר – בדומה לשורש ריבועי של מספר. אז, אם יש משהו שאתם צריכים לזכור לגבי לוגריתמים, זה שהם לוקחים מספר והופכים אותו לקטן יותר מהמקור (ראו איור 4). עכשיו, בצורה זהה לזה ששורשים ריבועיים הם הפעולה ההופכית של להעלות משהו בריבוע, לוגריתמים הם הפעולה ההופכית של להעלות מספר בחזקת משהו. זה לא קשה כמו שזה נשמע. קל יותר להסביר את זה עם דוגמה. בואו נסתכל על המשוואה הבאה:
2x = 1024
היינו רוצים לפתור את המשוואה הזו עבור x. אז אנחנו שואלים את עצמינו: מה הוא המספר שעבורו אם נעלה את 2 בחזקה שלו נקבל 1024? המספר הזה הוא 10. ואכן, 210 = 1024, שזה דבר שקל לבדוק. לוגריתמים עוזרים לנו לייצג את הבעיה הזו באמצעות סימון חדש. במקרה הזה, 10 הוא הלוגריתם של 1024, ואנחנו יכולים לרשום אותו כ־log( 1024 ) ולקרוא את זה כ"הלוגריתם של 1024". מכיוון שהשתמשנו ב־2 כבסיס, הלוגריתמים האלו נקראים לוגריתמים בבסיס 2. ישנם לוגריתמים בבסיסים אחרים, אבל אנחנו נשתמש רק בלוגריתמים בבסיס 2 במאמר הזה. אם אתם תלמידים שמשתתפים בתחרויות בינלאומיות ואתם לא יודעים לוגריתמים, אני ממליץ לכם בחום להתאמן על לוגריתמים אחרי שתסיימו לקרוא את המאמר הזה. במדעי המחשב, לוגריתמים בבסיס 2 נפוצים בהרבה יותר מאשר לוגריתמים מסוגים אחרים. הסיבה לכך היא שיש לנו שני ערכים שונים: 0 ו־1. אנחנו גם נוטים לחתוך בעיה גדולה לחצאים, מהם יש תמיד שניים. מהסיבות האלו תצטרכו לדעת על לוגריתמים בבסיס 2 כדי להמשיך עם המאמר הזה.
תרגיל 7
פתרו את המשוואות המופיעות מטה. ציינו איזה לוגריתם אתם מוצאים בכל אחד מהמקרים. השתמשו רק בלוגריתמים מבסיס 2.
- 2x = 64
- (22)x = 64
- 4x = 4
- 2x = 1
- 2x + 2x = 32
- (2x) * (2x) = 64
פתרון
מדובר ביישום ישיר של ההגדרות שהופיעו למעלה.
- בעזרת ניסוי וטעייה אנחנו יכולים למצוא ש־x = 6, ולכן log( 64 ) = 6.
- כאן אנחנו שמים לב ש־(22)x, לפי חוקי חזקות, יכול להיכתב גם כ־22x. אז יש לנו את השוויון 2x = 6 מכיוון ש־log( 64 ) = 6 מהתוצאה הקודמת ולכן x = 3.
- אם נשתמש בידע שלנו מהשוויון הקודם, נוכל לכתוב 4 כ־22, ולכן המשוואה שלנו הופכת להיות (22)x = 4 שזה כמו 22x = 4. נשים לב ש־log( 4 ) = 2 מכיוון ש־22 = 4 ולכן אנחנו יכולים להגיד ש־2x = 2. אז x = 1. קל לראות את זה עוד מהמשוואה הראשונית, שכן המעריך 1 גורם לצד למספר כלשהו להיות כמו התוצאה של פעולת החזקה.
- זכרו שמשהו בחזקת 0 יוצא 1. אז יש לנו log( 1 ) = 0 מכיוון ש־20 = 1, אז x = 0.
- כאן יש לנו סכום ולכן אנחנו לא יכולים לבצע את הלוגריתם ישירות. עם זאת, אנחנו משתמשים בכך ש־2x + 2x זה כמו 2 * (2x). אז הכפלנו עוד פעם בשתיים, ולכן התוצאה שווה ל־2x + 1. עכשיו כל מה שאנחנו צריכים לעשות זה לפתור את השוויון 2x + 1 = 32. נמצא ש־log( 32 ) = 5, ולכן x + 1 = 5. לכן x = 4.
- אנחנו מכפילים חזקות של 2 אחת בשנייה, אז אנחנו יכולים לאחד אותן מכיוון ש־(2x) * (2x) הן כמו 22x. כל מה שאנחנו צריכים לעשות עכשיו זה לפתור את המשוואה 22x = 64 שכבר פתרנו למעלה, ולכן x = 3.
כלל אצבע: עבור אלגוריתמים שמומשו ב־C++ בתחרויות, אחרי שניתחתם את הסיבוכיות, אתם יכולים לקבל הערכה גסה של כמה מהירה התוכנית שלכם אם תצפו ממנה לבצע בערך 1,000,000 פעולות לשנייה, כשכמות הפעולות שאתם צריכים לספור נמדדת לפי הפונקציה של ההתנהגות האסימפטוטית של האלגוריתם שלכם. לדוגמה, עבור Θ( n ) לאלגוריתם לוקח כשנייה לעבד את הקלט, עבור n = 1,000,000.
סיבוכיות רקורסיבית
עכשיו בואו נסתכל על סיבוכיות רקורסיבית. פונקציה רקורסיבית היא פונקציה שקוראת לעצמה. האם אנחנו יכולים לנתח את הסיבוכיות שלה? הפונקציה הבאה שכתובה ב־Python מחשבת את העצרת של מספר נתון. ניתן למצוא את העצרת של מספר שלם חיובי אם מכפילים אותו עם כל המספרים החיוביים לפניו. לדוגמה, החזקה של 5 היא 5 * 4 * 3 * 2 * 1. אנחנו כותבים את זה כ־"!5" ומבטאים את זה כ"חמש עצרת" (אנשים מסוימים מעדיפים לבטא את זה בכך שהם פשוט צועקים בקול "חמש!!!").
def factorial( n ):
if n == 1:
return 1
return n * factorial( n - 1 )
בואו ננתח את הסיבוכיות של הפונקציה הזו. בתוך הפונקציה הזו אין לולאות, אבל גם ניתן להגיד שהסיבוכיות שלה אינה קבועה. מה שאנחנו צריכים לעשות כאן על מנת למצוא את הסיבוכיות שלה זה שוב להתחיל ולספור הוראות. קל לראות שאם אנחנו מעבירים n מסוים עבור הפונקציה הזו, היא תתבצע n פעמים. אם אתם לא בטוחים בכך, תריצו אותה עכשיו באופן "ידני" עבור n = 5 כדי לוודא שהיא באמת עובדת. לדוגמה, עבור n = 5 היא תתבצע 5 פעמים, מכיוון שהיא תמשיך להפחית את n ב־1 בכל קריאה. אנחנו יכולים לראות, אם כך, שהפונקציה הזו היא Θ( n ).
אם אתם לא בטוחים בעובדה הזו, זכרו שאתם תמיד יכולים למצוא את הסיבוכיות המדויקת אם תספרו את כמות ההוראות בתוכנית. אם אתם רוצים, אתם יכולים לנסות לספור את כמות ההוראות שמתבצעות בתוכנית הזו על מנת למצוא את f( n ) ולראות שהיא אכן לינארית (זכרו שלינארית אומר Θ( n )).
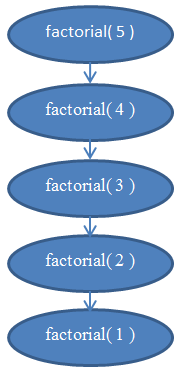
ראו את איור 5 שהוא תרשים שיעזור לכם להבין את הקריאות שמתבצעות לרקורסיה כאשר factorial( 5 ) נקראת.
זה אמור להבהיר למה הפונקציה הזו היא בעלת סיבוכיות לינארית.
סיבוכיות לוגריתמית
בעיה מפורסמת במדעי־המחשב היא חיפוש של ערך בתוך מערך. פתרנו את הבעיה הזו מוקדם יותר עבור מקרה כללי. הבעיה הזו הופכת להיות מעניינת יותר כשיש לנו מערך ממוין, ואנחנו רוצים למצוא בתוכו ערך מסוים. דרך אחת לעשות את זה נקראת חיפוש בינארי. אנחנו מסתכלים על האיבר האמצעי במערך, אם אנחנו מוצאים את הערך שם, סיימנו. במידה ולא, אם הערך שמצאנו שם גדול מהערך שאנחנו מחפשים אחריו, אנחנו נדע שהאיבר שלנו נמצא בצד השמאלי של המערך. אחרת, אנחנו יודעים שהוא בצד הימני של המערך. אנחנו יכולים להמשיך ולחתוך את המערכים הקטנים האלו לחצאים, עד שיש לנו איבר אחד שעליו אנחנו מסתכלים. הנה הדרך בפסאודו־קוד:
def binarySearch( A, n, value ):
if n = 1:
if A[ 0 ] = value:
return true
else:
return false
if value < A[ n / 2 ]:
return binarySearch( A[ 0...( n / 2 - 1 ) ], n / 2 - 1, value )
else if value > A[ n / 2 ]:
return binarySearch( A[ ( n / 2 + 1 )...n ], n / 2 - 1, value )
else:
return true
הפסאודו־קוד הזה הוא פישוט של המימוש האמיתי. בפועל, קל לתאר את השיטה הזו מאשר לממש אותה, שכן מתכנתים צריכים להתגבר על בעיות מימוש שונות. ישנן שגיאות של סטייה באחד מגודלי המערך, וחלוקה ב־2 לא תמיד מייצרת מספר שלם ולכן חייבים לעגל כלפי מעלה או כלפי מטה את הערך. אבל אנחנו יכולים להניח שלמטרות שלנו החלוקה תמיד תצליח, ואנחנו נניח שהמימוש שלנו לוקח בחשבון את ענייני הסטייה ב־1, מכיוון שאנחנו רק רוצים לנתח את הסיבוכיות של השיטה הזו. אם מעולם לא יצא לכם לממש חיפוש בינארי לפני־כן, יתכן שתרצו לעשות את זה בשפה המועדפת עליכם. זו באמת השקעה משתלמת.
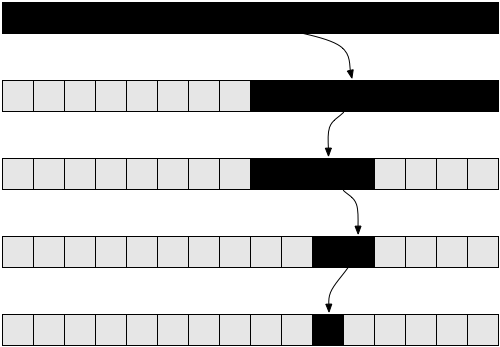
ראו את איור 6 שיעזור לכם להבין איך עובד חיפוש בינארי.
אם אתם לא בטוחים שהדרך הזו באמת עובדת, קחו רגע לנסות להריץ אותה באופן ידני עבור דוגמה פשוטה, ושכנעו את עצמכם שזה באמת יכול לעבוד.
עכשיו בואו ננסה לנתח את האלגוריתם הזה. שוב, יש לנו אלגוריתם רקורסיבי במקרה הזה. נניח, עבור הפשטות, שהמערך תמיד נחתך בדיוק באמצע, תוך שאנחנו מתעלמים מהחלק בקריאה הרקורסיבית שאומר + 1 ומהחלק שאומר - 1. בשלב הזה אתם כבר אמורים להיות משוכנעים ששינוי קטן כמו להתעלם מחלקים כמו + 1 וכמו - 1 לא ישפיעו על התוצאה של הסיבוכיות. זו עובדה שהיינו צריכים להוכיח בדרך כלל אם היינו רוצים להיות זהירים מנקודת מבט מתמטית, אבל מעשית זה ברור מאליו אינטואיטיבית. נניח שהמערך שלנו הוא בגודל שהוא חזקה שלמה של 2, לצורך הפשטות. ההנחה הזו שוב לא משנה את התוצאות הסופיות של ניתוח הסיבוכיות. המצב הגרוע ביותר עבור הבעיה הזו הוא כשהערך שאנחנו מחפשים לא נמצא כלל במערך שלנו. במקרה הזה, אנחנו נתחיל לחפש במערך בגודל n בקריאה הראשונה לרקורסיה, ואז נקבל מערך שגודלו n / 2 בקריאה הבאה. בקריאה שאחרי נקבל מערך שגודלו n / 4, לאחריה נקבל קריאה למערך בגודל n / 8 וכך הלאה. בכלליות, המערך שלנו נחצה לשניים בכל קריאה, עד שאנחנו מגיעים ל־1. אז, בואו נרשום את מספר האיברים במערך עבור כל קריאה:
שימו לב שבחזרור ה־i, במערך שלנו יש n / 2i איברים. זה קורה מכיוון שבכל חזרור אנחנו חותכים את המערך שלנו לחצי, משמע שאנחנו מחלקים את מספר האיברים שלו בשתיים. זה מיתרגם להכפלת המכנה ב־2. אם אנחנו עושים את זה i פעמים, אנחנו מקבלים n / 2i. עכשיו, ההליך הזה ממשיך וככל ש־i גדל אנחנו מקבלים מספר קטן יותר של איברים במערך עד שאנחנו מגיעים לחזרור האחרון בו נשאר איבר אחד. אם נרצה למצוא את i כדי לראות באיזה חזרור זה יקרה, אנחנו צריכים לפתור את המשוואה הבאה:
1 = n / 2i
המשוואה תהיה נכונה כאשר הגענו לקריאה האחרונה של הפונקציה binarySearch(), לא במקרה הכללי. לכן, פתירת המשוואה עבור i תעזור לנו למצוא באיזה חזרור הרקורסיה תסתיים. אם נכפיל את שני הצדדים ב־2i נקבל:
2i = n
עכשיו המשוואה הזו אמורה להיות מוכרת אם קראתם את החלק על לוגריתמים למעלה. נפתור עבור i:
i = log( n )
זה אומר לנו שמספר החזרורים הנדרשים כדי לבצע חיפוש בינארי הוא log( n ), כאשר n הוא מספר האיברים במערך המקורי.
אם אתם חושבים על זה, זה די הגיוני. לדוגמה, קחו את n = 32, מערך בגודל 32 איברים. כמה פעמים נצטרך לחתוך אותו לחצי כדי לקבל רק איבר אחד? נחשב: 32 → 16 → 8 → 4 → 2 → 1. עשינו את זה 5 פעמים, שהוא גם הלוגריתם של 32. לכן, הסיבוכיות של חיפוש בינארי היא Θ( log( n ) ).
התוצאה האחרונה מאפשרת לנו להשוות חיפוש בינארי עם חיפוש לינארי, השיטה הקודמת שלנו. זה ברור שמכיוון ש־log( n ) קטן בהרבה מ־n, הגיוני להסיק שחיפוש בינארי היא שיטה מהירה בהרבה לחיפוש בתוך מערך מאשר חיפוש לינארי, ולכן זו מומלץ לשמור על המערכים שלנו ממוינים אם אנחנו מעוניינים לבצע בהם הרבה חיפושים.
כלל אצבע: שיפור של זמן ריצה אסימפטוטי בתוכנית לרוב מגדיל בצורה משמעותית את הביצועים שלה, יותר מאשר כל שיפור "טכני" קטן כמו שימוש בשפת תכנות מהירה יותר.
מיון אופטימלי
ברכות. עכשיו יש ברשותכם ידע על סיבוכיות של אלגוריתמים, על התנהגות אסימפטוטית של פונקציות ועל הסימון O גדולה. אתם גם יודעים להבין באופן אינטואיטיבי שהסיבוכיות של אלגוריתם מסוים היא O( 1 ), O( log( n ) ), O( n ), O( n2 ) וכן הלאה. אתם מכירים את הסימונים o, O, ω, Ω ו־Θ ויודעים מה זה ניתוח המקרה הגרוע ביותר. אם הגעתם עד כאן, המדריך הזה כבר השיג את מטרתו.
החלק האחרון הזה אינו בגדר חובה. הוא דורש קצת מעורבות, אז תרגישו בנוח לדלג עליו אם אתם מרגישים המומים ממה שהולך פה. החלק הזה ידרוש מכם להתרכז ולהשקיע כמה רגעים בלפתור את התרגילים. עם זאת, הוא יספק לכם שיטה מאוד שימושית בניתוח סיבוכיות של אלגוריתמים שיכולה להיות עוצמתית מאוד, כך שבהחלט שווה להבין אותו.
למעלה, הסתכלנו על מימוש של מיון שנקרא מיון בחירה. הזכרנו שמיון בחירה הוא לא האופטימלי. אלגוריתם מיטבי (או אלגוריתם אופטימלי) הוא אלגוריתם שפותר את הבעיה בצורה הטובה ביותר, משמע, שאין אלגוריתמים טובים ממנו לפתרון הבעיה. זה אומר שכל האלגוריתמים האחרים שפותרים את הבעיה הזו גרועים מהאלגוריתם הזה, או לכל היותר טובים כמוהו. יכולים להיות הרבה אלגוריתמים מיטביים לבעיה שחולקים את אותה סיבוכיות. בעיית המיון יכולה להיפתר במספר רב של דרכים. אנחנו יכולים להשתמש ברעיון של החיפוש הבינארי על מנת למיין מהר מערכים. שיטת המיון הזו נקראת מיון מיזוג.
על מנת לבצע מיון מיזוג, אנחנו קודם נצטרך לבנות פונקציית עזר, בה נשתמש כדי לעשות את המיון עצמו. אנחנו ניצור פונקציית מיזוג בשם merge שתקבל שני מערכים ששניהם כבר ממוינים, ונאחד אותם למערך גדול וממוין. אפשר לעשות את זה בקלות:
def merge( A, B ):
if empty( A ):
return B
if empty( B ):
return A
if A[ 0 ] < B[ 0 ]:
return concat( A[ 0 ], merge( A[ 1...A_n ], B ) )
else:
return concat( B[ 0 ], merge( A, B[ 1...B_n ] ) )
הפונקציה concat לוקחת איבר, ה"ראש", ומערך, ה"זנב", ובונה ומחזירה מערך חדש שמכיל את ה"ראש" כאיבר הראשון במערך החדש ואת הזנב הנתון כשאר האיברים במערך. לדוגמה, concat( 3, [ 4, 5, 6 ] ) יחזיר [ 3, 4, 5, 6 ]. אנחנו נשתמש בסימונים A_n ו־B_n כדי לציין את הגדלים של מערכים A ו־B בהתאמה.
תרגיל 8
וודאו שהפונקציה הכתובה למעלה באמת מבצעת מיזוג. כתבו אותה מחדש בשפת התכנות המועדפת עליכם בעזרת חזרורים (השתמשו בלולאות for) במקום להשתמש ברקורסיה.
ניתוח של האלגוריתם הזה מגלה שהוא רץ ב־Θ( n ), כש־n זה הגודל של המערך שיוצא כתוצאה (n = A_n + B_n).
תרגיל 9
ודא שזמן הריצה של המיזוג בפונקציה merge הוא Θ( n ).
בעזרת הפונקציה הזו אנחנו יכולים לבנות אלגוריתם מיון טוב יותר. הרעיון הוא כזה: נפצל את המערך לשני חלקים. נסדר את שני החלקים באופן רקורסיבי, ואז נמזג את שני החלקים המסודרים למערך אחד. בפסאודוקוד:
def mergeSort( A, n ):
if n = 1:
return A # it is already sorted
middle = floor( n / 2 )
leftHalf = A[ 1...middle ]
rightHalf = A[ ( middle + 1 )...n ]
return merge( mergeSort( leftHalf, middle ), mergeSort( rightHalf, n - middle ) )
את הפונקציה הזו יותר קשה להבין ממה שעברתם עליו עד עכשיו, אז התרגיל הבא עלול לקחת לכם כמה דקות.
תרגיל 10
ודאו את הנכונות של mergeSort. משמע, בדקו האם mergeSort המוגדרת מעלה באמת מסדרת כראוי את המערך שהיא מקבלת. אם אתם נתקלים בבעיות בלהבין למה זה עובד, נסו דוגמה של מערך קטן והריצו אותה "ידנית". כשאתם מריצים אותה ידנית, ודאו ש־leftHalf ו־rightHalf הם מה שאתם מקבלים אם אתם חותכים את המערך בערך באמצע; זה לא חייב להיות בדיוק באמצע אם המערך בגודל אי־זוגי של איברים (לכן יש את פונקציית העיגול כלפי מטה, floor).
כדוגמה אחרונה, בואו ננתח את הסיבוכיות של mergeSort. בכל שלב ב־mergeSort אנחנו מפצלים את המערך לשני חלקים בגודל שווה, בדומה למה שעשינו ב־binarySearch. עם זאת, במקרה הזה, אנחנו שומרים על שני החצאים במהלך הריצה. לאחר מכן אנחנו מחילים את האלגוריתם בצורה רקורסיבית בתוך כל חצי. לאחר שהרקורסיה מחזירה ערך, אנחנו מחילים את פעולת המיזוג (merge) על התוצאה, שרצה בזמן Θ( n ).
אם כן, נפצל את המערך המקורי לשני מערכים שגודל כל אחד מהם הוא n / 2. לאחר מכן נמזג את המערכים האלו, פעולה שהיא מיזוג של n איברים ולכן רצה בזמן Θ( n ).
הביטו באיור 7 כדי להבין את הרקורסיה הזו.
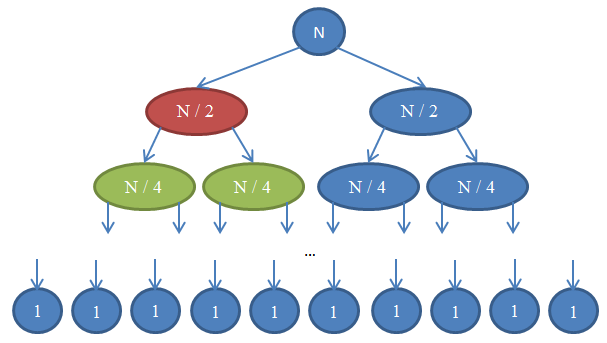
בואו נראה מה הולך כאן. כל עיגול מסמל קריאה לפונקציה mergeSort. המספר שכתוב בעיגול מורה על הגודל של המערך שעובר מיון. העיגול הכחול העליון הוא הקריאה המקורית ל־mergeSort, שם אנחנו ממיינים מערך בגודל n. החצים מצביעים על הקריאות הרקורסיביות שנעשות בין הפונקציות. הקריאה המקורית ל־mergeSort מבצעת שתי קריאות ל־mergeSort על שני מערכים, כל אחד מהם הוא n / 2. זה מסומן על־ידי שני החצים העליונים. בתורם, כל אחת מהקריאות האלו עושה שתי קריאות משל עצמה ל־mergeSort, שמטרתן למיין ולמזג שני מערכים בגודל n / 4, וכך זה ממשיך עד שאנחנו מגיעים למערכים בגודל 1. התרשים הזו נקרא עץ רקורסיה מכיוון שהוא מדגים כיצד הרקורסיה מתנהגת, והוא נראה כמו עץ (השורש למעלה והעלים למטה, כך שבמציאות זה נראה כמו עץ הפוך).
שימו לב איך בכל שורה בתרשים שלמעלה, מספר האיברים הוא n. כדי לראות את זה, העיפו מבט בכל שורה בנפרד. השורה הראשונה כוללת רק קריאה אחת ל־mergeSort עם מערך בגודל n, אז מספר האיברים הכולל הוא n. השורה השנייה מכילה שתי קריאות ל־mergeSort, כל אחת מהן בגודל n / 2. אבל n / 2 + n / 2 = n, ולכן שוב מספר האיברים בשורה הזו הוא n. בשורה השלישית יש לנו 4 קריאות, כל אחת מוחלת על מערך בגודל n / 4, כך שיש לנו מספר איברים ששווה ל־n / 4 + n / 4 + n / 4 + n / 4 = n. אז שוב קיבלנו n איברים. עכשיו שימו לב שבכל שורה בתרשים הפונקציה שקוראת תצטרך לבצע פעולת מיזוג (merge) על האיברים שחזרו מהפונקציות שלהם היא קראה. לדוגמה, העיגול האדום צריך לסדר n / 2 איברים. על מנת לעשות זאת, הוא מחלק את המערך שגודלו n / 2 לשני מערכים בגודל n / 4, וקורא ל־mergeSort באופן רקורסיבי על־מנת שתסדר אותם. פעולת המיזוג הזו דורשת לסדר n / 2 איברים. בכל שורה בעץ שלנו, המספר הכולל של האיברים שממוזגים הוא n. בשורה שזה עתה חקרנו, הפונקציה שלנו תמזג n / 2 איברים והפונקציה שמימינה (בכחול) גם תמזג n / 2 איברים בעצמה. זה יוצר n איברים בסך הכול שצריכים להיות ממוזגים בשורה שעליה אנחנו מסתכלים.
לפי הטענה הזו, הסיבוכיות של כל שורה היא Θ( n ). אנחנו יודעים שמספר השורות בתרשים הזה, שגם נקרא העומק של עץ הרקורסיה, יהיה log( n ). ההיגיון מאחורי זה הוא בדיוק אותו היגיון בו השתמשנו כשניתחנו את החיפוש הבינארי. יש לנו log( n ) שורות וכל אחת מהן רצה ב־Θ( n ), ולכן הסיבוכיות של mergeSort היא Θ( n * log( n ) ). זה הרבה יותר טוב מ־Θ( n2 ), שזה מה שקיבלנו כשהשתמשנו במיון בחירה (זכרו ש־log ( n ) הוא הרבה יותר קטן מ־n, ולכן n * log( n ) הוא הרבה יותר קטן מ־n * n = n2). אם זה נשמע לכם מסובך, אל תדאגו: זה לא פשוט בפעם הראשונה כשרואים את זה. בקרו שוב בחלק הזה וקראו את הטענות כאן אחרי שמימשתם מיון מיזוג בשפת התכנות האהובה עליכם, ווידאתם שהמימוש שלכם עובד.
כמו שראיתם בדוגמה האחרונה, ניתוח סיבוכיות מאפשר לנו להשוות אלגוריתמים כדי לראות מי מהם טוב יותר. תחת הנסיבות האלו, אנחנו יכולים להיות די בטוחים שמיון מיזוג יבצע טוב יותר מאשר מיון בחירה עבור מערכים גדולים. יהיה קשה להסיק מסקנה שכזו אם לא היה לנו את הרקע התיאורטי של אלגוריתמים שפיתחנו. במציאות, אכן משתמשים באלגוריתמים שממיינים בזמן ריצה Θ( n * log( n ) ). לדוגמה, הליבה של לינוקס משתמשת באלגוריתם מיון שנקרא מיון ערימה, שלו יש זמן ריצה זהה לזה של מיון מיזוג שחקרנו כאן, משמע, Θ( n * log( n ) ) ולכן הוא מיטבי. שימו לב שלא הוכחנו שאלגוריתמי המיון האלו מיטביים. אם נרצה לעשות את זה נצטרך לערב טיעונים מתמטיים קצת יותר מורכבים, אבל היו סמוכים ובטוחים כי האלגוריתמים האלו לא יכולים להיות טובים יותר מבחינת הסיבוכיות שלהם.
מאחר שסיימתם את המדריך הזה, האינטואיציה שפיתחתם בנוגע לניתוח סיבוכיות צריכה לעזור לכם לעצב תוכניות מהירות יותר ולרכז את מאמצי הייעול שלכם בדברים שבאמת חשובים במקום בדברים קטנים שאינם חשובים, ולתת לכם לעבוד בצורה יותר פרודקטיבית. בנוסף, השפה המתמטית והסימונים שפיתחנו במאמר הזה כמו O גדולה (Big O) שימושיים בתקשורת עם מהנדסי תוכנה אחרים כשאתם רוצים לדבר על זמן הריצה של אלגוריתמים, בתקווה שתוכלו לעשות את זה עם הידע החדש שרכשתם.
על־אודות
מאמר זה כפוף לרישיון Creative Commons 3.0 Attribution. זה אומר שאתם יכולים להעתיק ולהדביק אותו, לשתף אותו, לפרסם אותו באתר שלכם, לשנות אותו ובאופן כללי לעשות איתו מה שאתם רוצים, כל עוד אתם מזכירים את שם הכותב המקורי. אני ממליץ לכם לפרסם את הכתבות שלכם תחת רישיון Creative Commons בעצמכם, כך שיהיה לאחרים קל יותר להפיץ ולשתף פעולה גם אצלכם. בצורה דומה, אני צריך להזכיר את המקורות שהשתמשתי בהם כאן. הסמלילים הקטנים שאתם רואים בדף הגיעו מ־fugue icons. התבנית המפוספסת היפהפייה שאתם רואים נוצרה על־ידי Lea Verou. והכי חשוב, את האלגוריתמים שאני יודע ושאפשרו לי לכתוב את המאמר לימדו אותי הפרופסורים שלי, Nikos Papaspyrou ו־Dimitris Fotakis.
אני כרגע מועמד לתואר שלישי בקריפטוגרפיה באוניברסיטת אתונה. כשכתבתי את המאמר הזה הייתי סטודנט לתואר ראשון בחשמל והנדסת מחשבים, וסיימתי את לימודי התואר השני שלי באוניברסיטה הטכנית הלאומית של אתונה, בהתמחות בתוכנה וכמאמן לאולימפיאדת מדעי־המחשב של יוון. בתעשייה, עבדתי כחבר־צוות בצוות ההנדסה שבנה את devianART, רשת חברתית של אמנים, בצוותי האבטחה של Google ושל Twitter, ובשני חברות הזנק, Zino ו־Kamibu, שם עסקנו ברשתות חברתיות ובפיתוח משחקים בהתאמה. עקבו אחריי ב־Twitter או ב־GitHub אם אתם אוהבים את הרעיון, או שלחו לי הודעת דואר־אלקטרוני אם אתם רוצים ליצור קשר. להרבה מתכנתים צעירים אין ידע טוב בשפה האנגלית. כתבו לי הודעת דואר אלקטרונית אם אתם רוצים לתרגם את המאמר הזה לשפתכם הטבעית כך שיותר אנשים יוכלו לקרוא אותו.
תודה שקראתם. לא שילמו לי על לכתוב את המאמר הזה, אז אם אהבתם אותו, שלחו לי הודעת דואר־אלקטרוני ותגידו שלום. אני נהנה לקבל תמונות ממקומות מסביב לעולם, אז תרגישו בנוח לצרף תמונה של עצמכם בעיר שלכם!
סימוכין
- Cormen, Leiserson, Rivest, Stein. Introduction to Algorithms, MIT Press.
- Dasgupta, Papadimitriou, Vazirani. Algorithms, McGraw-Hill Press.
- Fotakis. Course of Discrete Mathematics at the National Technical University of Athens.
- Fotakis. Course of Algorithms and Complexity at the National Technical University of Athens.

