Доступное введение в анализ сложности алгоритмов.
Dionysis "dionyziz" Zindros <dionyziz@gmail.com>Перевод: Y. E. T.
- English
- Ελληνικά
- македонски
- Español
- Nederlands
- עברית
- Português
- srpskohrvatski
- Українська
- Русский
- Help translate
Вступление
Многие из современных программистов — создающих классные и чрезвычайно полезные приложения, которые мы видим в Интернете или используем ежедневно — не обладают теоретическими знаниями в области информатики. Такие программисты всё же прекрасные созидающие специалисты, и мы благодарны им за то, что они делают.
Однако теоретические знания имеют прикладное значение и могут быть использованы для решения практических задач. Эта статья предназначена для программистов, владеющих своим искусством, но не имеющих образования в области информатики. В статье будет описан один из самых прагматичных инструментов информатики: анализ сложности алгоритмов. Я работал как в академической среде, так и в сфере построения прикладного программного обеспечения, и обнаружил, что этот инструмент по-настоящему полезен. Так что я надеюсь, что после прочтения этой статьи и вы сможете применять его для улучшения кода. Вы также познакомитесь с такими общепринятыми в информатике терминами, как «О‐большое», «асимптотическое поведение» и «анализ наихудшего случая».
Этот текст также предназначен для учеников средних и старших классов, участвующих в Международной олимпиаде по информатике или в других подобных соревнованиях. Таким образом, эта статья не требует от вас глубоких математических знаний и предоставит необходимый теоретический материал для дальнейшего изучения алгоритмов. Я сам участвовал в подобных соревнованиях, и поэтому настоятельно рекомендую внимательно прочитать весь вводный материал и попытаться полностью его понять, так как он необходим для дальнейшего изучения алгоритмов и более сложных методов их анализа.
Я верю, что этот текст будет полезен программистам практикам, не имеющим больших теоретических знаний (некоторые из самых вдохновляющих инженеров программного обеспечения не получали высшего образования). Однако имейте в виду, что статья написана и для учеников, так что время от времени она может несколько напоминать учебник. Также некоторые из тем могут оказаться для вас слишком простыми; к примеру, если вы уже сталкивались с ними. В такой ситуации переходите к следующей теме. Последующие разделы больше углубляются в рассматриваемые вопросы и приобретают теоретическую окраску, так как ученикам, участвующим в соревнованиях, необходимы эти знания. Как бы то ни было, все рассматриваемые здесь темы полезно знать, они доступны для понимания, так что скорее всего достойны вложения вашего времени.
В этой статье вы найдете ссылки на интересный материал, выходящий за рамки рассматриваемой темы. Если вы профессиональный программист, скорее всего вы уже знакомы с большей частью такого материала. Если вы ученик, участвующий в соревнованиях, изучение дополнительного материала поможет вам познакомиться с другими областями информатики и программирования и, возможно, расширить круг ваших интересов.
Многие программисты и ученики считают, что анализ сложности алгоритмов труден для понимания. Они боятся его или даже полностью его избегают, думая, что это бесполезная тема. На самом деле, «O‐большое» и анализ сложности алгоритмов не так трудны для понимания, как это может казаться. Анализ сложности алгоритмов — это всего лишь способ оценить скорость работы программы или алгоритма, так что это весьма практический инструмент. Давайте начнём с небольшой мотивации.

Мотивация
Мы уже знаем о существовании инструментов, измеряющих скорость работы кода. Эти программы называются профилировщиками (англ. profilers). Профилировщики измеряют длительность работы кода в миллисекундах и помогают выявлять узкие места (англ. bottleneck) в работе кода, для дальнейшей его оптимизации. При всей полезности таких инструментов, профилировщики не имеют отношения к сложности алгоритмов. Анализ сложности алгоритмов был разработан для сравнения алгоритмов на уровне их идей, игнорируя несущественные детали: используемый язык программирования, оборудование, набор команд центрального процессора. Мы хотим сравнить сущность алгоритмов: идеи, каким образом должно быть произведено вычисление. Подсчёт миллисекунд не поможет нам справиться с такой задачей. Вполне вероятно, что плохой алгоритм, написанный на низкоуровневом языке программирования — к примеру на ассемблере — отработает гораздо быстрее, чем хороший алгоритм, написанный на высокоуровневом языке программирования — к примеру на Python или Ruby. Итак, настало время дать определение понятию «более хороший алгоритм».
Так как алгоритмы — это программы, занятые вычислениями (в отличие от других задач, выполняемых компьютерами: сетевых, ввода и вывода данных пользователем), анализ сложности позволяет нам измерить скорость работы программы. Примеры сугубо вычислительных операций включают в себя операции с числами, представленными в форме с плавающей запятой (такие как сложение и умножение); поиск по резидентной базе данных (англ. in-memory database); нахождение самого короткого пути для персонажа, управляемого искусственным интеллектом (Рисунок 1); или поиск в тексте с использованием регулярных выражений. Очевидно, что вычислительные задачи встречаются повсеместно в компьютерных программах.
Анализ сложности также позволяет описать, как алгоритм ведёт себя при увеличении размера входных данных. Как поведёт себя алгоритм, получив другое количество входных данных? Если наш алгоритм отрабатывает за 1 секунду, получив 1000 единиц входных данных, то как он поведёт себя, получив в два раза больше данных? Будет ли он работать с той же скоростью или в два раза медленнее, или в четыре раза медленнее? Анализ сложности позволяет предсказывать поведение алгоритма, что важно для прикладного программирования. Предположим, мы написали алгоритм для веб-приложения, хорошо работающий с данными 1000 пользователей, и измерили как быстро он справляется со своей задачей. Тогда анализ сложности алгоритма позволит нам оценить насколько быстро он будет работать, получив данные 2000 пользователей. Для соревнований по информатике, анализ сложности даёт понимание, сколько времени понадобится нашему коду, чтобы обработать самые большие тестовые данные, используемые для проверки правильности работы нашей программы. Таким образом, если мы измерим скорость работы программы с малым количеством входных данных, тогда мы сможем оценить, какова будет скорость её работы с большим количеством данных. Начнём с простого примера: нахождение самого большого элемента в массиве данных.
Подсчёт инструкций
В этой статье примеры кода будут написаны на разных языках программирования. Не унывайте, если вы не знакомы с какими-либо из них. Все примеры будут простыми, без использования эзотерических возможностей языков, так что человек, знакомый с программированием, сможет понять все примеры без проблем. Если вы ученик, участвующий в соревнованиях, вы вероятнее всего знакомы с C++, так что примеры и для вас должны быть понятны. Ученикам я рекомендую попрактиковаться с примерами, написав их на C++.
Мы можем найти наибольший элемент массива используя показанный ниже фрагмент Javascript кода. Пусть нам дан массив данных A с размером n >= 1. Тогда:
var M = A[ 0 ];
for ( var i = 0; i < n; ++i ) {
if ( A[ i ] >= M ) {
M = A[ i ];
}
}
Сначала мы подсчитаем количество базовых команд в этом фрагменте кода. Мы проведём такой подсчёт только один раз. Необходимость в нём отпадёт по мере разбора теории, так что наберитесь немного терпения. Во время анализа этого фрагмента кода мы хотим разбить его на простые команды: те, которые могут быть выполнены процессором напрямую (или близко к этому). Предположим, что наш процессор может выполнять такие операции как одну команду:
- Присвоить значение переменной.
- Найти значение заданного элемента в массиве.
- Сравнить два значения.
- Увеличить значение на единицу (инкремент).
- Произвести базовые арифметические действия (сложение, вычитание).
Мы предположим, что ветвление (выбор между частями кода в теле if или else) происходит мгновенно, и не будем подсчитывать эти команды. Рассмотрим первую строку кода, показанного выше:
var M = A[ 0 ];
Эта строка содержит две команды: одна находит элемент массива A[ 0 ], другая присваивает найденную величину переменной M. Алгоритм всегда выполняет эти две команды, независимо от значения n. Цикл for тоже выполняется всегда и даёт нам ещё две команды: присваивания и сравнения.
i = 0;
i < n;
Они отработают до первой итерации цикла for. После каждой итерации цикла for отработают ещё две команды: инкремента i и сравнения (для проверки, остаёмся ли мы в цикле):
++i;
i < n;
Так что (если мы проигнорируем тело цикла) количество команд выполняемых этим алгоритмом равно 4 + 2n. А именно, 4 команды в начале цикла for и 2 команды в завершении каждой итерации (всего осуществляется n итераций). Теперь мы можем определить математическую функцию f( n ), которая соотносит n с количеством команд, выполняемых алгоритмом. При пустом теле цикла for, f( n ) = 4 + 2n.
Анализ наихудшего случая
А теперь посмотрим на тело цикла for. Здесь всегда осуществляются поиск в массиве и операция сравнения:
if ( A[ i ] >= M ) { ...
То есть в теле цикла выполняются две команды. Однако выполнение или невыполнение команд в теле if зависит от значений элементов массива. Если A[ i ] >= M, тогда отработают ещё две команды: поиска в массиве и присваивания:
M = A[ i ]
Но теперь мы больше не можем легко определить f( n ), потому что количество команд зависит не только от n, но и от значений вводимых данных. Например, при A = [ 1, 2, 3, 4 ], алгоритму понадобится выполнить больше команд, чем при A = [ 4, 3, 2, 1 ]. При анализе алгоритмов часто рассматривается наихудший сценарий. Какие входные данные самые неблагоприятные для нашего алгоритма? В каком случае нашему алгоритму понадобится выполнить максимальное количество операций? Для рассматриваемого примера самый плохой вариант — это получить массив, отсортированный по возрастанию, например: A = [ 1, 2, 3, 4 ]. В таком случае с каждой новой итерацией значение i-го элемента массива будет присвоено M, а это максимальное количество выполняемых команд. Для таких случаев у теоретиков есть затейливое название: анализ наихудшего случая; а ведь это всего лишь рассмотрение самого неудачного варианта. Итак, при наихудшем случае в теле цикла for отработает 4 команды. Итого, f( n ) = 4 + 2n + 4n = 6n + 4. Функция f при заданной проблеме с размером n даёт нам количество команд, исполняемых в наихудшем случае.
Асимптотическое поведение
Полученная выше функция даёт нам довольно ясное представление о скорости работы алгоритма. Однако, как я и обещал, нам не понадобится каждый раз заниматься трудоёмким подсчётом количества команд в программе. К тому же количество реальных команд, выполняемых процессором, зависит от компилятора нашего языка программирования и от типа самого процессора. Как мы уже говорили, мы проигнорируем эту разницу. Сейчас мы пропустим нашу функцию «f» через «фильтр», который поможет нам избавиться от несущественных деталей, игнорируемых во время анализа.
Функция f( n ) = 6n + 4 состоит из двух членов: 6n и 4. При анализе сложности нас интересует, что происходит с функцией подсчёта команд при увеличении количества входных данных n. Этот подход хорошо соответствует анализу поведения при наихудшем случае: нам интересно узнать, как алгоритм поведёт себя в «плохих» условиях (при необходимости обработать тяжёлую задачу). Заметьте, что это очень удобно при сравнении алгоритмов между собой. Если один алгоритм «побеждает» другой при большом количестве входных данных, тогда наиболее вероятно, что более быстрый алгоритм останется таковым и при меньшем количестве входных данных. Поэтому мы пренебрежём теми членами функции, которые растут медленно, и оставим те, которые растут очень быстро при увеличении n. Явно, что 4 останется равным 4 при любом значении n. При этом 6n будет становиться больше и больше с увеличением значения n, так что именно 6n будет иметь всё большее и большее значение с увеличением входных данных. Следовательно, мы можем пренебречь значением 4 и записать нашу функцию в такой форме: f( n ) = 6n.
И это здравый подход, ведь 4 — всего лишь «константа инициализации». Разным языкам программирования может понадобиться разное количество времени для инициализации. Например, языку Java требуется значительное количество времени для запуска виртуальной машины. А так как мы игнорируем различия между языками программирования, то разумно будет пренебречь и константой 4.
Ещё один элемент, которым можно пренебречь — это постоянный множитель 6. Таким образом, нашу функцию можно записать в таком виде: f( n) = n. Как видите, мы очень сильно упростили функцию подсчёта команд. И это снова выглядит как разумный подход, принимая во внимание, что разные языки программирования компилируются по-разному. Например, язык C, выполняя инструкцию A[ i ], не удостоверяется, что значение i находится в диапазоне размера массива. В то же время Паскаль делает такую проверку. Другими словами, последующий фрагмент кода на языке Паскаль:
M := A[ i ]
эквивалентен такому коду на языке C:
if ( i >= 0 && i < n ) {
M = A[ i ];
}
Так что во время подсчёта команд приемлемо ожидать разные множители от разных языков программирования. В нашем примере для языка Паскаль используется самый примитивный компилятор, без каких-либо оптимизаций. В таком случае Паскалю необходимо 3 команды для каждого запроса к массиву данных; вместо лишь 1 команды, выполняемой языком C. Опуская соответствующий множитель, мы поступаем согласно уже принятому нами подходу игнорирования разницы между языками программирования и анализа самой сущности алгоритмов.
Описанный выше фильтр «пренебрежения множителями и константами» имеет название: асимптотическое поведение. Так, асимптотическое поведение функции f( n ) = 2n + 8 описывается функцией f( n ) = n. Говоря математическим языком, нам интересен предел функции f при n, стремящемся к бесконечности. (Если вам не понятен смысл этой фразы, не беспокойтесь: достаточно, что вы ознакомились с этой формулировкой. Примечание: при строгом математическом подходе мы не смогли бы пренебречь константами; но для задач в сфере информатики мы ими пренебрегаем по причинам, описанным выше). А теперь проработаем пару примеров, чтобы привыкнуть к уже описанным концепциям.
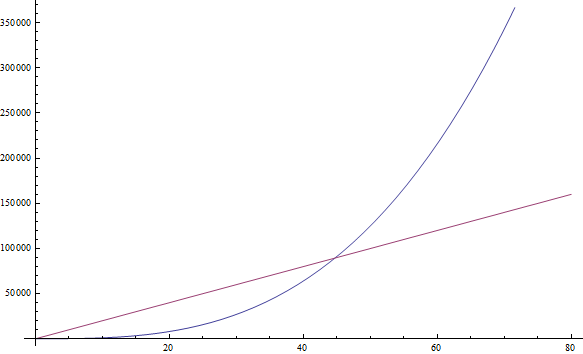
Найдем асимптотическое поведение следующих функций:
f( n ) = 5n + 12 даёт f( n ) = n.
Следуя ходу мысли, изложенному выше.
f( n ) = 109 даёт f( n ) = 1.
Мы пренебрегаем множителем 109 * 1, но должны оставить 1 для обозначения, что функция обладает не нулевым значением.
f( n ) = n2 + 3n + 112 даёт f( n ) = n2
n2 растёт быстрее, чем 3n, при достаточно большом значении n.
f( n ) = n3 + 1999n + 1337 даёт f( n ) = n3
Множитель 1999 довольно велик, но мы всё же можем найти достаточно большое значение n, такое, что n3 будет больше, чем 1999n. А так как мы заинтересованы в поведении при очень больших значениях n, то мы оставляем только n3 (смотрите Рисунок 2).
f( n ) = n +
 даёт f( n ) = n
даёт f( n ) = nИз-за того, что n растёт быстрее чем
 по мере увеличения n.
по мере увеличения n.
Попробуйте найти асимптотическое поведение следующих функций самостоятельно:
Упражнение 1
- f( n ) = n6 + 3n
- f( n ) = 2n + 12
- f( n ) = 3n + 2n
- f( n ) = nn + n
(Запишите ваши результаты; решения даны ниже.)
Если у вас возникли проблемы с какой-либо из функций, подставьте в неё большое значение n и сравните, какой из членов становится больше. Довольно-таки просто, ага?
Сложность
Так как мы можем пренебречь всеми декоративными константами, то довольно легко определить асимптотическое поведение функции подсчёта команд. На самом деле, асимптотическое поведение любой программы без циклов будет f( n ) = 1, так как количество команд, выполняемых такой программой, всегда равно какой-то константе (это не касается случая рекурсии, рассматриваемого ниже). Асимптотическое поведение любой программы с одним циклом, проходящем от 1 до n, будет f( n ) = n, так как такая программа будет вызывать какое-то постоянное количество команд до начала цикла, после завершения цикла и внутри цикла (команды внутри цикла всего будут вызываться n раз).
Такой подход должен быть на порядок проще, чем громоздкий подсчёт всех команд программы. Так что давайте взглянем на пару примеров, чтобы привыкнуть к нему. Следующая программа, написанная на языке PHP, проверяет, находится ли заданное значение в массиве A с размером n:
<?php
$exists = false;
for ( $i = 0; $i < n; ++$i ) {
if ( $A[ $i ] == $value ) {
$exists = true;
break;
}
}
?>
Такой метод поиска значения в массиве данных называется линейным поиском. Это подходящее название, так как асимптотическое поведение этой программы описывается функцией f( n ) = n (мы дадим точное определение «линейности» в следующем разделе). Обратите внимание на инструкцию «break», которая может вызвать более раннее завершение работы программы (возможно, сразу же на первом шаге цикла). Вспомните, что нас интересует только самый плохой сценарий. Для данной программы — это отсутствие искомого элемента в массиве A. Так что мы всё ещё имеем f( n ) = n.
Упражнение 2
Используя данную выше программу на языке PHP, подсчитайте количество команд, вызываемых этой программой в наихудшем случае, и выведите функцию подсчёта команд f( n ), как мы это уже делали на примере Javascript программы. Затем проверьте, что асимптотически мы получаем сложность, описываемую функцией f( n ) = n.
Взгляните на программу, написанную на языке Python. Эта программа складывает значения двух элементов массива и присваивает результат сложения новой переменной:
v = a[ 0 ] + a[ 1 ]
Эта программа содержит постоянное количество команд, так что f( n ) = 1.
Следующая программа на языке C++ проверяет, содержит ли вектор (причудливый массив) A с размером n два одинаковых значения:
bool duplicate = false;
for ( int i = 0; i < n; ++i ) {
for ( int j = 0; j < n; ++j ) {
if ( i != j && A[ i ] == A[ j ] ) {
duplicate = true;
break;
}
}
if ( duplicate ) {
break;
}
}
Эта программа содержит вложенные циклы. В таком случае асимптотическое поведение описывается функцией f( n ) = n2.
Подсказка: Простые программы могут быть проанализированы путём подсчёта циклов. Единичный цикл с n шагами приводит к сложности f( n ) = n. Дополнительный вложенный цикл приводит к сложности f( n ) = n2. Цикл внутри цикла внутри цикла имеет сложность f( n ) = n3.
Если программа вызывает функцию в теле цикла, и если нам известно количество команд, исполняемых этой функцией, тогда несложно подсчитать количество команд, выполняемых всей программой. Действительно, взгляните на такой пример на языке C:
int i;
for ( i = 0; i < n; ++i ) {
f( n );
}
Если нам известно, что f( n ) выполняет n команд, значит мы знаем, что количество команд, выполняемых всей программой, асимптотически равно n2, так как функция f( n ) будет вызвана точно n раз.
Подсказка: Если нам дана последовательность циклов for, то самый медленный из них определяет асимптотическое поведение всей программы. Два вложенных цикла, за которыми следует одиночный цикл, асимптотически равны просто двум вложенным циклам, потому что вложенные циклы доминируют над одиночными.
Теперь перейдём к причудливому способу записи, используемому теоретиками. Когда мы выводим асимптотическое поведение, мы можем сказать, что наша программа — это Θ( f( n ) ). Например, программы выше — это, соответственно, Θ( 1 ), Θ( n2 ) и Θ( n2 ). Θ( n ) произносится как «тета от эн». Иногда мы говорим, что f( n ), изначальная функция подсчёта команд программы, включающая в себя константы, — это Θ( что-то ). Например, можно сказать, что функция f( n ) = 2n — это Θ( n ). Ещё один вариант записи: 2n ∈ Θ( n ), произносится как "два эн есть тета от эн". Не смущайтесь, ведь всё, что эта форма записи говорит: мы подсчитали количество команд, выполняемых программой, и оно равно 2n; значит асимптотическое поведение алгоритма можно описать как n (опустив константу 2). Следующие математические выражения используют новый способ записи:
- n6 + 3n ∈ Θ( n6 )
- 2n + 12 ∈ Θ( 2n )
- 3n + 2n ∈ Θ( 3n )
- nn + n ∈ Θ( nn )
Кстати, это и есть ответы к упражнению 1.
Мы называем эту функцию — я имею в виду ту функцию, которую мы разместили Θ( здесь ) — временнОй сложностью или просто сложностью алгоритма. Так, алгоритм с Θ( n ) имеет сложность n. У нас также есть специальные названия для Θ( 1 ), Θ( n ), Θ( n2 ) и Θ( log( n ) ), потому что это очень часто встречающиеся классы сложности. Алгоритм с Θ( 1 ) называется алгоритмом константного времени, Θ( n ) — линейным алгоритмом, Θ( n2 ) — квадратичным, Θ( log( n ) ) — логарифмическим (не беспокойтесь, если вы не знакомы с последним термином: логарифмы будут рассмотрены чуть ниже).
Подсказка: Чем больше Θ, тем медленнее работает программа.

«O‐большое»
На самом деле иногда нелегко определить поведение алгоритма, используя данный выше подход. Особенно это касается более сложных примеров. Как бы то ни было, всегда возможно оценить, в каких рамках ведёт себя алгоритм. Это облегчает нам жизнь, так как освобождает от необходимости определять точную скорость работы алгоритма. Всё, что нам необходимо сделать — это определить границы поведения алгоритма. Этот подход доступно объясняется на следующем примере.
Для обучения алгоритмам обычно используется задача сортировки. В этой задаче даётся массив A с размером n (звучит знакомо?), и нас просят написать программу, которая упорядочивает элементы массива. Это интересная задача: она имеет практическое применение в реальных системах. Например, менеджер файлов должен отсортировать файлы по наименованию, для упрощения навигации пользователя. Или другой пример: видеоигре необходимо отсортировать 3D объекты мира на основании их расположения относительно игрока, для определения какие из объектов видны, а какие нет (расчёт области видимости, смотрите Рисунок 3). Самые близкие к игроку объекты будут видны, а более удалённые могут быть скрыты объектами между ними. Сортировка становится ещё более интересной из-за наличия различающихся по эффективности алгоритмов сортировки. И, наконец, это довольно доступная для объяснения и понимания задача. Так что и мы сейчас напишем код сортировки массива.
Далее показан неэффективный способ реализации сортировки массива, написанный на языке Ruby. (Конечно, Ruby предоставляет встроенные функции для сортировки массивов, которые и следует использовать в большинстве случаев. Встроенные функции работают быстрее, чем показанная ниже программа, предложенная в сугубо иллюстрационных целях).
b = []
n.times do
m = a[ 0 ]
mi = 0
a.each_with_index do |element, i|
if element < m
m = element
mi = i
end
end
a.delete_at( mi )
b << m
end
Такой метод называется сортировкой выбором (англ. selection sort). Сортировка выбором находит наименьшее значение массива (мы обозначили массив как a, минимальное значение m, индекс этого значения mi), добавляет найденное значение в конец массива b и удаляет это значение из заданного массива a. Затем алгоритм снова находит минимальное значение среди оставшихся элементов массива a, добавляет его в конец массива b (теперь массив b содержит два отсортированных элемента) и удаляет из массива a. Перечисленные шаги повторяются до тех пор, пока изначально заданный массив не станет пустым, а все его элементы окажутся перенесёнными в новый, отсортированный, массив. Этот пример содержит вложенные циклы. Внешний цикл отрабатывает n раз, а внутренний массив отрабатывает один раз для каждого элемента массива a. Изначально массив a содержит n элементов, однако мы удаляем из него один элемент на каждом шаге внешнего цикла. Так что внутренний цикл отрабатывает n раз во время первого шага внешнего цикла, затем n - 1 раз, затем n - 2 раз и так далее, до последнего шага внешнего цикла, на котором внутренний цикл отработает лишь один раз.
Оценить сложность этой программы немного труднее, так как нам надо подсчитать сумму 1 + 2 + ... + (n - 1) + n. Но мы точно можем найти «верхнюю границу» для этой программы. Ведь мы можем изменить нашу программу (вы можете проделать эту операцию в уме, без написания кода) таким образом, чтобы она стала хуже, чем она есть на самом деле, и затем найти сложность такой выведенной программы. Если мы найдём сложность выведенной программы, то сложность оригинальной программы будет такой же или даже меньшей. То есть, если окажется, что выведенная программа довольно эффективна (эта эффективность по определению хуже, чем у нашей изначальной программы), то мы сможем сделать вывод, что оригинальная программа тоже имеет хорошую эффективность. По крайней мере, не меньше (или даже больше), чем у выведенной — ухудшенной — программы.
А теперь подумаем о способе отредактировать программу из примера так, чтобы упростить оценку её сложности. При этом удерживайте мысль о том, что мы можем изменять её лишь в сторону ухудшения, то есть сделать так, чтобы она выполняла ещё больше команд (чтобы оценка сложности правильно соотносилась с изначальной программой). Очевидно, что мы можем изменить количество шагов, выполняемых внутренним циклом программы так, чтобы их всегда было точно n, вместо уменьшающегося количества шагов. Некоторые из этих повторений будут бесполезными для сортировки, но упростят нам анализ сложности алгоритма. Если мы сделаем это простое изменение, тогда новый, только что сконструированный, алгоритм будет оцениваться как Θ( n2 ), потому что он будет состоять из двух вложенных циклов, каждый из которых повторяется n раз. В такой ситуации мы говорим, что оригинальный алгоритм имеет сложность O( n2 ). O( n2 ) произносится как «большое о от эн в квадрате». Это означает, что наша программа асимптотически не хуже, чем n2 (она может быть лучше или равняться n2). Между прочим, если наша программа в действительности имеет сложность Θ( n2 ), то это соответствует и O( n2 ). Чтобы помочь вам это осмыслить, представьте, как вы изменяете изначальную программу совсем немного, но всё же ухудшаете её производительность, например добавив несущественную команду в начало программы. Таким способом вы измените функцию подсчёта команд на константу, игнорируемую при определении асимптотического поведения. Отсюда следует, что программа Θ( n2 ) также является и O( n2 ).
Но вот программа со сложностью O( n2 ) может не иметь Θ( n2 ). Например, любая программа с Θ( n ) — это также O( n2 ), вдобавок к O( n ). Представим, что программа Θ( n ) — это простой цикл for, повторяющийся n раз. Тогда мы можем ухудшить её, обернув во второй цикл for, тоже повторяющийся n раз, и получив в результате программу с f( n ) = n2. Обобщим: любая программа со сложностью Θ( a ) также имеет и сложность O( b ), если b растёт быстрее, чем a. Заметьте, что изменения, внесённые в программу, не должны привести к правильно работающей программе или программе, аналогичной изначальной. Ей только необходимо выполнять больше команд, чем выполняется оригинальной версией программы. Изменённую программу мы используем сугубо для подсчёта команд, а не для решения изначальной задачи.
Итак, безопаснее будет сказать, что наша программа имеет сложность O( n2 ): мы проанализировали алгоритм и нашли, что он никогда не работает хуже, чем n2. Такая формулировка даёт нам хорошую оценку скорости работы нашей программы. Следующие упражнения даны для привыкания к новой нотации.
Упражнение 3
Определите, какие из формулировок верны:
- Алгоритм с Θ( n ) имеет сложность O( n )
- Алгоритм с Θ( n ) имеет сложность O( n2 )
- Алгоритм с Θ( n2 ) имеет сложность O( n3 )
- Алгоритм с Θ( n ) имеет сложность O( 1 )
- Алгоритм с O( 1 ) имеет сложность Θ( 1 )
- Алгоритм с O( n ) имеет сложность Θ( 1 )
Решения
- Это правда, так как наша изначальная программа имеет сложность Θ( n ). Мы можем получить O( n ) даже не меняя программу.
- Так как n2 хуже, чем n, то и это утверждение верно.
- Так как n3 хуже, чем n2, то это утверждение верно.
- Так как 1 не хуже, чем n, то это неверное утверждение. Если программа асимптотически выполняет n команд (линейное количество), то мы не можем усложнить её и получить всего лишь одну команду, выполняемую асимптотически (константное количество).
- Это верно, так как эти сложности равнозначны.
- Это может быть как верным, так и ложным утверждением. В общем случае оно ложно. Если алгоритм имеет сложность Θ( 1 ), тогда он конечно же имеет сложность O( n ). Но при O( n ), он не обязательно будет иметь сложность Θ( 1 ). Например, алгоритм Θ( n ) имеет сложность O( n ), но не Θ( 1 ).
Упражнение 4
Используйте формулу суммы арифметической прогрессии для доказательства, что данная выше программа имеет сложность не только O( n2 ), но также Θ( n2 ). Если вы не знаете, что такое арифметическая прогрессия, загляните в Википедию — это легко.
Так как «О‐большое» алгоритма описывает верхнюю границу реальной сложности алгоритма, описываемой Θ, то иногда можно сказать, что Θ описывает точные границы сложности. Если известно, что найденная граница сложности не является точной, то в таких случаях можно использовать нотацию «o-малое». Например, если алгоритм имеет сложность Θ( n ), тогда его точная сложность соответствует n. Следовательно, этот алгоритм имеет сложность и O( n ), и O( n2 ). Граница O( n ) является точной, но граница O( n2 ) — нет. Так что можно написать, что этот алгоритм имеет сложность o( n2 ) — произносится «o малое от эн в квадрате» — для иллюстрации того, что эта граница неточная. Обычно лучше знать точные границы алгоритмов, ведь таким образом больше становится известно о поведении алгоритма. Однако точные границы не всегда легко определить.
Упражнение 5
Определите, какие из перечисленных границ точные, а какие нет. Проверьте, все ли границы верны. Используйте «О‐большое» для иллюстрации неточных границ.
- Алгоритм с Θ( n ) и верхней границей O( n ).
- Алгоритм с Θ( n2 ) и верхней границей O( n3 ).
- Алгоритм с Θ( 1 ) и верхней границей O( n ).
- Алгоритм с Θ( n ) и верхней границей O( 1 ).
- Алгоритм с Θ( n ) и верхней границей O( 2n ).
Решения
- В этом случае Θ и O сложности одинаковы, так что это точная граница.
- Здесь мы видим, что O даёт большую сложность, чем Θ, так что эта граница неточная (сложность O( n2 ) дала бы точную границу). Следовательно, мы можем записать сложность алгоритма как o( n3 ).
- Снова мы видим, что O даёт большую сложность, чем Θ. Так что это неточная граница (граница O( 1 ) была бы точной). Следовательно, можно обозначить, что граница O( n ) неточная, записав её в виде o( n ).
- Должно быть мы ошиблись при выводе этой границы; она неверна. Для алгоритма с Θ( n ) невозможно, чтобы верхняя граница была O( 1 ), ведь n имеет большую сложность, чем 1. Помните, что «О‐большое» описывает верхнюю границу.
- Может показаться, что это неточная граница, однако это не так. Эта граница на самом деле точная. Вспомните, что асимптотическое поведение 2n есть n; и что O и Θ описывают асимптотическое поведение. Из этого следует, что O( 2n ) = O( n ), и значит это точная граница, ведь она равна Θ.
Подсказка: Вывести O-сложность легче, чем Θ-сложность.
Возможно, к этому моменту вас уже утомили все эти новые формы записи. Всё же познакомимся с ещё двумя символами и затем перейдём к примерам. Эти символы будет легко понять на базе уже знакомых вам Θ, O и o. Новые символы не будут использоваться в оставшейся части статьи, однако хорошо бы их знать, и сейчас подходящий момент для такого знакомства. В примере выше, мы изменяли программу так, чтобы она работала хуже (добавив команды для замедления её работы), и выводили таким образом «О‐большое». «O» предоставляет ценную информацию, на базе которой можно доказывать, что наша программа работает достаточно хорошо. Если проделать обратное действие: улучшить программу, а затем найти её сложность, то можно использовать форму записи «Ω». Ω описывает сложность таким образом, что мы знаем: наша программа не будет работать лучше этой сложности. Такое знание полезно в тех случаях, когда мы хотим показать, что программа работает медленно или что анализируемый алгоритм не эффективен для решения определённой задачи. Например, алгоритм со сложностью Ω( n3 ) означает, что этот алгоритм не работает лучше, чем n3 (он как минимум настолько плох). То есть этот алгоритм может иметь сложность Θ( n3 ), или Θ( n4 ), или даже хуже. Итак, Ω даёт нам нижнюю границу сложности алгоритма. Наподобие «ο-малое», можно использовать запись в виде «ω-малое» в тех случаях, когда известно, что граница неточная. Например, алгоритм Θ( n3 ) имеет ο( n4 ) и ω( n2 ). Ω( n ) произносится как «омега большое от эн», а ω( n ) произносится как «омега малое от эн».
Упражнение 6
Определите точные и неточные О и Ω границы для следующих Θ сложностей.
- Θ( 1 )
- Θ(
 )
) - Θ( n )
- Θ( n2 )
- Θ( n3 )
Решения
- Точными границами являются O( 1 ) и Ω( 1 ). Неточной O-границей может быть O( n ). Вспомните, что O даёт нам верхнюю границу. Так как n имеет большую сложность, чем 1, то эту неточную границу можно также записать в виде o( n ). Неточная Ω граница не существует, так как мы не можем упростить сложность, равную 1.
- Точные границы равны Θ-сложности, так что это, соответственно, O(
 ) и Ω(
) и Ω(  ). В роли неточной границы можно использовать O( n ), так как n больше чем
). В роли неточной границы можно использовать O( n ), так как n больше чем  . Зная, что это неточная верхняя граница, можно использовать форму записи o( n ). Для неточной нижней границы можно использовать Ω( 1 ), что также можно записать в виде ω( 1 ).
. Зная, что это неточная верхняя граница, можно использовать форму записи o( n ). Для неточной нижней границы можно использовать Ω( 1 ), что также можно записать в виде ω( 1 ). - Точными границами являются O( n ) и Ω( n ). Неточными границами могут быть ω( 1 ) и o( n3 ). Это довольно плохой выбор границ, так как они сильно отличаются от заданной сложности. Однако они соответствуют данным нами определениям, так что могут быть использованы.
- Точными границами являются O( n2 ) и Ω( n2 ). В качестве неточных границ можно снова использовать ω( 1 ) и o( n3 ), как и в предыдущем примере.
- Точными границами являются O( n3 ) и Ω( n3 ), соответственно. Неточными границами могут быть ω(
 n2 ) и o(
n2 ) и o(  n3 ). Хотя эти границы неточные, всё же они лучше тех, что были даны выше.
n3 ). Хотя эти границы неточные, всё же они лучше тех, что были даны выше.
Причина использования O и Ω вместо Θ — хотя O и Ω тоже могут определять точные границы — заключается в том, что не всегда известно, является ли найденная граница точной (вероятно в ситуации, когда мы просто не хотим дотошно анализировать алгоритм).
Если вы не запомнили все упомянутые символы и их точное использование, не беспокойтесь. Вы всегда можете вернуться к этой статье и уточнить их данные. Самыми важными символами являются O и Θ.
Также заметьте, что хотя Ω определяет поведение нижней границы функции (т.е. функция была улучшена посредством урезания количества выполняемых команд), мы всё ещё ссылаемся на анализ «наихудшего случая». Так происходит потому, что программе даётся самый плохой вариант из возможных входящих данных; её поведение анализируется исходя из этого предположения.
Следующая таблица показывает только что представленные символы и соответствующие им обычные математические символы, используемые для сравнения чисел. Буквы греческого алфавита используются вместо более привычных символов для указания, что мы занимаемся сравнением асимптотического поведения, а не чисел.
| Асимптотическое сравнение | Численное сравнение |
|---|---|
| Алгоритм с o( что-то ) | Число < что-то |
| Алгоритм с O( что-то ) | Число ≤ что-то |
| Алгоритм с Θ( что-то ) | Число = что-то |
| Алгоритм с Ω( что-то ) | Число ≥ что-то |
| Алгоритм с ω( что-то ) | Число > что-то |
Подсказка: Хотя все символы O, o, Ω, ω и Θ очень полезны, «О‐большое» используется наиболее часто. Его проще определить, чем Θ, и оно более практично, чем Ω.
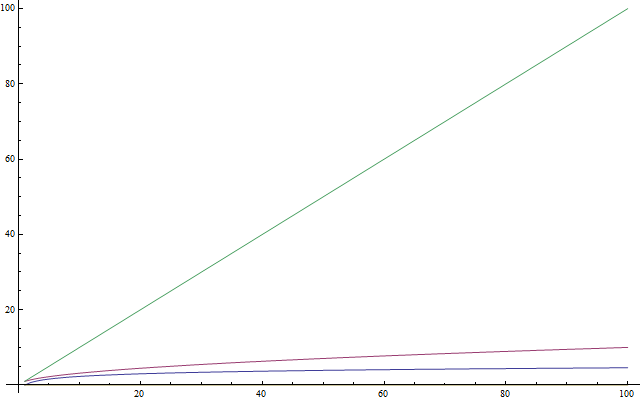
Логарифмы
Если вы знаете, что такое логарифм, то можете пропустить этот раздел. Этот ознакомительный раздел написан для людей, не знакомых с логарифмами; а также для тех, кто давно с ними не сталкивался. Этот текст также предназначен для учеников, которые ещё не изучали логарифмы в школе. Знание логарифмов очень важно, так как они постоянно встречаются при анализе сложности алгоритмов. Логарифм — это операция, применённая к числу так, что число значительно уменьшается (совсем как извлечение корня). Извлечение квадратного корня является операцией, обратной от возведения числа в квадрат. Точно так же, логарифм — это обратная операция от возведения числа в какую-либо степень. На самом деле всё гораздо проще, чем звучит. Лучше рассмотрим на таком примере:
2x = 1024
Для того, чтобы решить это уравнение и найти значение x, мы спрашиваем себя: в какую степень нужно возвести 2, чтобы получить 1024? Это будет число 10. Действительно, мы получаем 210 = 1024, что легко подтвердить. Логарифмы помогают записать эту задачку в другой нотации. В данном случае, 10 является логарифмом 1024, что записывается как log( 1024 ) (произносится как «логарифм 1024»). Так как мы используем 2 в основании логарифма, то такие логарифмы называются двоичными. Существуют логарифмы и с другими основаниями, но в этой статье мы используем только логарифмы с основанием 2. Если вы ученик, участвующий в международных соревнованиях и не знакомый с логарифмами, то я крайне рекомендую вам попрактиковаться после прочтения этой статьи. В информатике двоичные логарифмы встречаются гораздо чаще других типов логарифмов. Всё из-за того, что в информатике мы в базе имеем только две сущности: 0 и 1; и предпочитаем разбивать большие проблемы на две части (повторяя это действие). Итак, для дальнейшего чтения статьи вам необходимы только двоичные логарифмы.
Упражнение 7
Решите уравнения. Запишите найденные логарифмы. Используйте только двоичные логарифмы.
- 2x = 64
- (22)x = 64
- 4x = 4
- 2x = 1
- 2x + 2x = 32
- (2x) * (2x) = 64
Решения
Просто используйте идеи, данные выше.
- Методом проб и ошибок находим, что x = 6 и log( 64 ) = 6.
- Согласно свойствам степеней, (22)x можно записать как 22x. Применяя предыдущий результат log( 64 ) = 6, мы получаем, что 2x = 6. Следовательно, x = 3.
- Используя данные из предыдущего уравнения, можно записать 4 в виде 22, так что уравнение преобразуется в (22)x = 4, а это то же самое, что 22x = 4. Затем мы замечаем, что log( 4 ) = 2 (ведь 22 = 4) и, следовательно, мы получаем, что 2x = 2. Итак, x = 1. Этот результат легко подтвердить, ведь возведение числа в степень 1 возвращает само число.
- Вспомним, что возведение числа в степень 0 даёт в результате 1. Значит, 20 = 1, то есть x = 0 и log( 1 ) = 0.
- Здесь мы имеем дело со сложением, так что не можем определить логарифм напрямую. Однако мы замечаем, что 2x + 2x это то же самое, что и 2 * (2x). Итак, у нас появился множитель 2, значит это выражение можно записать в виде 2x + 1. Теперь нам осталось только решить уравнение 2x + 1 = 32. Мы находим, что log( 32 ) = 5 и тогда x + 1 = 5. Следовательно, x = 4.
- Мы умножаем результаты возведения 2 в степень x, значит мы можем объединить множители, заметив, что (2x) * (2x) равно 22x. Затем всё, что нам надо сделать — это решить уравнение 22x = 64, которое мы уже решали выше с результатом x = 3.
Подсказка: В случае с алгоритмами, написанными для соревнований (на языке C++), как только сложность была проанализирована, можно получить ориентировочную оценку скорости работы вашей программы. Ожидайте производительность около 1,000,000 операций в секунду (для операций, количество которых определено функцией асимптотического поведения алгоритма). Например, алгоритм со сложностью Θ( n ) отрабатывает приблизительно за секунду при размере входных данных n = 1,000,000.
Сложность рекурсивных алгоритмов
Рассмотрим рекурсивные функции. Рекурсивной называется функция, которая вызывает саму себя. Поддаётся ли анализу сложность таких функций? Следующая функция, написанная на языке Python, вычисляет факториал заданного числа. Факториал положительного целого числа находится посредством умножения данного числа с каждым предшествующим ему положительным целым числом. Например, факториал числа 5 равен 5 * 4 * 3 * 2 * 1. Факториал записывается в виде «5!», что произносится как «пять факториал» (хотя некоторые люди предпочитают просто громко выкрикивать «ПЯТЬ!!!»)
def factorial( n ):
if n == 1:
return 1
return n * factorial( n - 1 )
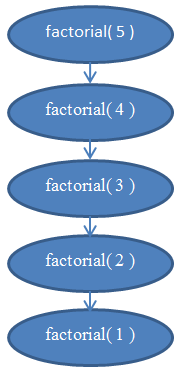
Проанализируем сложность этой функции. Она не содержит циклов, но её сложность всё же не является константной. Для определения сложности нам надо снова заняться подсчётом команд, выполняемых программой. Очевидно, что если передать в эту программу некоторое значение n, то она отработает n раз. Если вы не уверены в этом, то «вручную» проверьте как работает функция при n = 5. Вы увидите, что функция будет вызвана 5 раз, каждый раз уменьшая n на 1. Итак, функция имеет сложность Θ( n ).
Если вы всё ещё не уверены в этом факте, вспомните, что всегда можно найти точную сложность, подсчитав количество выполняемых команд. Если хотите, попробуйте подсчитать реальное количество команд, выполняемых функцией факториала, выведите f( n ) и убедитесь, что она в действительности линейна (напоминаю, что линейная функция соответствует Θ( n )).
Рисунок 5 содержит диаграмму, которая поможет вам понять, как выглядит рекурсия при вызове функции factorial( 5 ), и почему эта функция имеет линейную сложность.
Логарифмическая сложность
Одна из классических задач в информатике — это поиск значения в массиве. Мы уже решали такую задачу для общего случая в одном из предыдущих разделов. Поиск в массиве становится очень занимательным, если нам дан уже отсортированный массив. Один из способов поиска в отсортированном массиве называется двоичным (бинарным). При таком способе проверяется элемент в середине массива: если найдено искомое значение, то поиск закончен; если значение середины больше, чем искомое, то поиск продолжится в левой части массива; иначе поиск продолжится в правой части массива. Затем полученные меньшие массивы снова разбиваются пополам, до тех пор, пока не останется лишь один элемент. Вот этот метод записанный с помощью псевдокода:
def binarySearch( A, n, value ):
if n = 1:
if A[ 0 ] = value:
return true
else:
return false
if value < A[ n / 2 ]:
return binarySearch( A[ 0...( n / 2 - 1 ) ], n / 2 - 1, value )
else if value > A[ n / 2 ]:
return binarySearch( A[ ( n / 2 + 1 )...n ], n / 2 - 1, value )
else:
return true
Этот псевдокод является упрощённой версией реальной реализации двоичного поиска. На практике двоичный поиск легче описать, чем реализовать в коде. Ведь программистам надо позаботиться о всех деталях: ошибках на единицу, необходимости округления результатов деления на 2 и т.д. Учитывая, что мы хотим лишь проанализировать сложность этого алгоритма, то для наших целей предположим, что он всегда работает успешно, и что реальная реализация позаботится о всех необходимых деталях. Если вы никогда не реализовывали двоичный поиск, рекомендую сделать это на вашем любимом языке программирования. Это действительно просвещающее занятие.
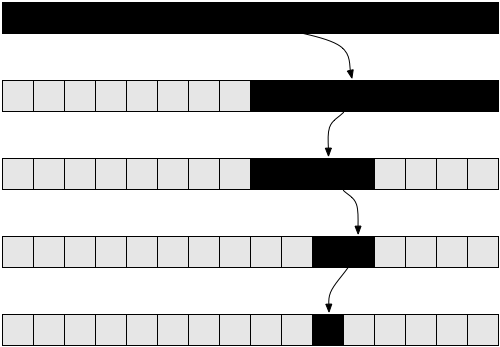
Рисунок 6 должен помочь вам понять, как работает двоичный поиск.
Если вы не уверены в работоспособности этого метода, возьмите простой пример и убедитесь, что он действительно работает.
Теперь попробуем проанализировать этот алгоритм. Здесь мы снова столкнулись с рекурсией. Предположим для простоты, что массив всегда делится ровно пополам, и проигнорируем + 1 и - 1 в рекурсивных вызовах. К этому моменту вы уже должны понимать, что такое маленькое изменение, как игнорирование + 1 и - 1, не повлияет на результаты анализа сложности. Нам пришлось бы доказывать этот факт, если бы мы хотели быть точными с математической точки зрения, но он и так интуитивно понятен. Также для простоты предположим, что нам дан массив с размером, равным степени 2. Это предположение тоже не повлияет на конечный результат анализа сложности. Наихудший случай этой задачи будет получен, если искомого значения вообще нет в массиве. В такой ситуации, при первом вызове функции, алгоритм получит массив с размером n. При следующем, рекурсивном, вызове: n / 2. Затем рекурсивный вызов получит массив с размером n / 4, за которым последует массив с размером n / 8 и так далее. Массив разбивается пополам при каждом новом рекурсивном вызове, пока не достигнет размера 1. Итак, запишем количество элементов массива при каждом вызове:
Обратите внимание, что на i-ом шаге массив имеет n / 2i элементов. Так происходит потому, что на каждом шаге массив разделяется пополам (другими словами, мы делим количество элементов массива на 2). Это действие можно выразить в виде умножения знаменателя на 2. При проделывании этой операции i раз, получаем n / 2i. Затем процедура деления продолжается, и для всё большего i мы получаем всё меньшее количество элементов, пока не достигнем последнего шага, на котором остаётся лишь 1 элемент. Если мы хотим найти i, чтобы узнать количество шагов работы программы, необходимо решить следующее уравнение:
1 = n / 2i
Это равенство станет верным лишь тогда, когда мы доберёмся до финального вызова функции binarySearch(), а не в общем случае. Найдя i, мы найдём, на каком шаге закончатся рекурсивные вызовы. Умножив обе стороны на 2i, получаем:
2i = n
Это уравнение должно выглядеть знакомым, если вы прочитали раздел о логарифмах. Решив уравнение для i, получаем:
i = log( n )
Это выражение говорит нам, что количество шагов, необходимое для осуществления двоичного поиска, равно log( n ), где n — количество элементов в данном массиве.
Такой результат выглядит вполне реалистично. Например, возьмите n = 32, массив с 32 элементами. Сколько раз нам придётся делить массив пополам, чтобы получить 1 элемент? Мы получим: 32 → 16 → 8 → 4 → 2 → 1 элементов, проделав 5 шагов, что и есть логарифм 32. Следовательно, сложность двоичного поиска равна Θ( log( n ) ).
Последний результат позволяет нам сравнить двоичный поиск с линейным поиском (предыдущий из рассмотренных нами методов). Очевидно, что log( n ) гораздо меньше n, так что мы заключаем, что двоичный поиск ищет элементы в массиве гораздо быстрее, чем линейный поиск. Также можно порекомендовать поддерживать массивы отсортированными, если необходимо часто осуществлять поиск по ним.
Подсказка: Улучшение асимптотического времени работы программ также часто значительно улучшает их время работы. И в гораздо больших масштабах, чем любые мелкие «технические» оптимизации, как, например, использование более быстрого языка программирования.
Оптимальная сортировка
Поздравляю. Теперь вы знаете, что такое анализ сложности алгоритмов, асимптотическое поведение и «О‐большое». Теперь вы знаете, что такое сложность алгоритма O( 1 ), O( log( n ) ), O( n ), O( n2 ) и так далее. Вы понимаете значение символов o, O, ω, Ω и Θ, и что такое анализ наихудшего случая. Раз вы добрались до этого этапа, значит учебный материал справился со своей задачей.
Этот финальный раздел необязателен для прочтения. Он более сложный, так что можете опустить его, если почувствуете, что вы перегружены. Этот раздел потребует от вас фокусировки для проработки дополнительных упражнений. При этом, он покажет вам очень полезный и потенциально мощный метод анализа сложности алгоритмов, что может стать стоящим вложением сил.
Выше мы рассматривали реализацию алгоритма под названием сортировка выбором. Было упомянуто, что сортировка выбором — это не оптимальный алгоритм. Оптимальным называется алгоритм, который решает задачу самым лучшим способом. Это означает, что все другие алгоритмы решения этой же задачи имеют сложность худшую или такую же, как у оптимального алгоритма. Для решения задач определённой сложности существует множество оптимальных алгоритмов. В частности, задача сортировки может быть решена оптимально разными способами. Например, мы можем использовать ту же идею, что лежит в основе двоичного поиска, чтобы получить быстрый способ сортировки, который называется сортировка слиянием (англ. merge sort).
Чтобы выполнить сортировку слиянием, сначала необходимо написать вспомогательную функцию, которая будет использована во время самой сортировки. Мы создадим функцию merge. Эта функция принимает два отсортированных массива и соединяет (англ. merge: слияние) их вместе, в один упорядоченный массив. Это легко сделать:
def merge( A, B ):
if empty( A ):
return B
if empty( B ):
return A
if A[ 0 ] < B[ 0 ]:
return concat( A[ 0 ], merge( A[ 1...A_n ], B ) )
else:
return concat( B[ 0 ], merge( A, B[ 1...B_n ] ) )
Функция concat принимает элемент («голову») и массив («хвост»), затем строит и возвращает новый массив, содержащий данную «голову» на первой позиции нового массива и элементы данного «хвоста» на остальных позициях массива. Например, concat( 3, [ 4, 5, 6 ] ) возвращает [ 3, 4, 5, 6 ]. Мы используем A_n и B_n для обозначения размеров массива A и B, соответственно.
Упражнение 8
Проверьте, что данная выше функция действительно выполняет слияние. Перепишите её на своём любимом языке программирования, используя цикл for вместо рекурсии.
Анализ этого алгоритма показывает, что время его выполнения Θ( n ), где n размер конечного массива (n = A_n + B_n).
Упражнение 9
Подтвердите, что время работы функции merge соответствует Θ( n ).
Используя эту функцию, можно построить улучшенный алгоритм сортировки. Базовая идея: делить массив на две части. Мы сортируем каждую из двух частей рекурсивно, а затем объединяем два отсортированных массива в один большой массив. Псевдокод:
def mergeSort( A, n ):
if n = 1:
return A # он уже отсортирован
middle = floor( n / 2 )
leftHalf = A[ 1...middle ]
rightHalf = A[ ( middle + 1 )...n ]
return merge( mergeSort( leftHalf, middle ), mergeSort( rightHalf, n - middle ) )
Эту функцию сложнее понять, чем то, что мы уже рассматривали, так что следующее упражнение может потребовать от вас больше времени.
Упражнение 10
Подтвердите, что функция mergeSort работает верно. А именно, что она действительно сортирует данный ей массив. Если вы не понимаете, как эта функция работает, то возьмите маленький массив и отследите «вручную» шаги, выполняемые mergeSort. При этом вы убедитесь, что leftHalf и rightHalf образуются при разбиении массива приблизительно посередине; разбиение не обязательно происходит точно в центре массива, если он содержит нечётное количество элементов (по этой причине используется функция floor).
В качестве последнего примера, подвергнем анализу сложность mergeSort. На каждом этапе выполнения mergeSort, массив разбивается на две части одинакового размера, совсем как в binarySearch. Однако в случае сортировки обе части сохраняются в процессе выполнения программы. Алгоритм применяется рекурсивно к каждой из частей. К результату выполнения рекурсий применяется операция merge, которая занимает Θ( n ) времени.
Итак, мы разбиваем данный массив на два массива, каждый с размером n / 2. Затем мы объединяем эти новые массивы, и это действие объединения n элементов требует Θ( n ) времени.
Взгляните на Рисунок 7, чтобы лучше понять происходящее.
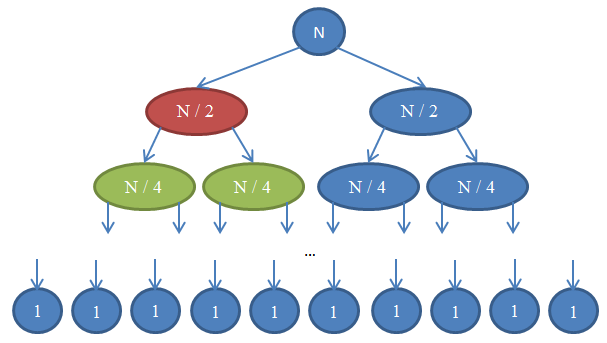
Посмотрим, что здесь происходит. Каждый круг отображает вызов функции mergeSort. Число внутри круга показывает размер сортируемого массива. Верхний синий круг — это изначальный вызов mergeSort, с задачей отсортировать массив размера n. Стрелки показывают рекурсивные вызовы функции. Изначальный вызов mergeSort делает два рекурсивных запроса к mergeSort, передавая каждый раз один массив с размером n / 2. Это действие отображается двумя стрелками вверху картинки. В свою очередь, каждый из вызовов функции делает ещё два вызова mergeSort, передавая каждый раз массив с размером n / 4 и так далее, пока не будут получены массивы с одним элементом. Такая схема называется рекурсивным деревом, потому что она отображает последовательность рекурсивных вызовов и похожа на дерево (точнее на перевёрнутое дерево, корень которого расположен вверху, а листья — внизу).
Обратите внимание, что в каждом ряду схемы общее количество элементов всегда равно n. Чтобы увидеть это, рассмотрите каждый ряд по отдельности. Первый ряд содержит только один вызов mergeSort с массивом размера n, так что общее количество элементов равно n. Второй ряд содержит два вызова mergeSort, где каждый из массивов имеет размер n / 2. Но n / 2 + n / 2 = n, так что снова общее количество элементов в этом ряду равно n. В третьем ряду мы видим 4 вызова, каждый из которых обрабатывает массив с размером n / 4, в результате давая общее количество элементов равное n / 4 + n / 4 + n / 4 + n / 4 = 4n / 4 = n. Итак, снова мы получаем n элементов. Теперь обратите внимание на то, что в каждом ряду схемы вызывающая функция должна будет выполнить операцию merge с элементами, возвращаемыми вызываемыми функциями. Например, круг, обозначенный красным цветом, должен отсортировать n / 2 элементов. Чтобы сделать это, он разбивает массив с размером n / 2 на два массива с размером n / 4, вызывает рекурсивно mergeSort для их сортировки (эти вызовы отображены кругами зелёного цвета), затем объединяет результаты в один массив. Операция объединения работает с n / 2 элементами. В каждом ряду нашего дерева общее количество объединяемых элементов равно n. В только что рассмотренном ряду функция объединяет n / 2 элементов; функция справа от неё (показана синим цветом) тоже объединяет n / 2 элементов. Итого получаем n объединяемых элементов в рассматриваемом ряду схемы.
В соответствии с этим рассуждением, каждый ряд имеет сложность Θ( n ). Нам известно, что количество рядов — известное под названием глубина дерева рекурсии — в данной схеме равно log( n ). Выводится это так же, как было сделано во время анализа сложности двоичного поиска. При количестве рядов log( n ), с каждым из них имеющим сложность Θ( n ), сложность mergeSort равна Θ( n * log( n ) ). Это гораздо лучший результат, чем Θ( n2 ), получаемый при использовании сортировки выбором (напоминаю, что log( n ) гораздо меньше n, так что n * log( n ) гораздо меньше n * n = n2). Если всё это звучит слишком сложно для вас, не беспокойтесь: такую информацию непросто понять с первого раза; прочитайте этот раздел ещё раз после того, как вы сами попробуете реализовать сортировку слиянием и убедитесь, что она работает.
Как было показано в последнем примере, анализ сложности позволяет нам сравнивать алгоритмы между собой для выяснения, какой из них работает лучше. Теперь мы вполне уверены, что для больших массивов данных сортировка слиянием работает быстрее, чем сортировка выбором. Прийти к этому выводу было бы тяжело без теоретических знаний, представленных в этой статье и необходимых для анализа алгоритмов. На практике действительно используют алгоритмы сортировки со временем работы Θ( n * log( n ) ). Например, ядро Linux использует алгоритм под названием пирамидальная сортировка (англ. heapsort), с тем же временем работы, что и у сортировки слиянием, рассмотренной нами — а именно Θ( n log( n ) ) — и являющимся оптимальным алгоритмом. Обратите внимание: мы не доказывали, что эти алгоритмы оптимальны. Для этого нам понадобилась бы более сложная математическая аргументация. Однако могу вас уверить, что с точки зрения сложности алгоритмов, сортировку нельзя сделать более эффективной.
Те знания об анализе сложности алгоритмов, которые вы приобрели во время чтения этой статьи, должны помочь вам создавать более быстрые программы и фокусировать усилия, прикладываемые для оптимизации кода, на действительно значимых вещах; таким образом делая вас более продуктивным. Также, математический язык и обозначения, с которыми вы познакомились, читая эту статью, помогут вам при общении с другими программистами. Теперь вы сможете обсуждать время работы алгоритмов, используя полученные знания.
Заключение
Эта статья лицензируется с Creative Commons 3.0 Attribution. Это означает, что статью можно копировать, распространять, публиковать на вашем ресурсе, изменять, в общем делать с ней всё, что хотите — при этом указав моё имя. Если вы основываете свою работу на моей статье, вы не обязаны, но я вам предлагаю тоже опубликовать ваш текст с лицензией Creative Commons, так как и другим людям будет проще делиться и сотрудничать. В соответствии с этим подходом, я упомяну работы, которые я использовал: fugue icons, Lea Verou. И, самое важное, я смог написать эту статью благодаря знаниям, полученным от профессоров Nikos Papaspyrou и Dimitris Fotakis.
Я являюсь PhD кандидатом в области криптографии в Афинском университете. Когда я писал эту статью, я был студентом факультета Электротехники и компьютерных наук Афинского национального технического университета, специализируясь в программном обеспечении и будучи тренером по Греческим соревнованиям в области информатики. Как программист практик, я был в команде, построившей deviantART, социальную сеть для художников; в командах безопасности в Google и Twitter; а также в стартапах Zino и Kamibu, которые занимались социальными сетями и разработкой видеоигр, соответственно. Если вам понравилась статья, подписывайтесь в Twitter или GitHub. Отправьте e-mail, если хотите связаться со мной или заняться переводом данного текста.
Благодарю вас за чтение. Мне не оплачивали написание этой статьи, так что если вам она понравилась, отправьте мне e-mail с приветствием. Мне нравится получать фотографии со всего мира. Если захотите, присылайте ваше фото в городе, где вы живёте!
Ресурсы
- Cormen, Leiserson, Rivest, Stein. Introduction to Algorithms, MIT Press.
- Dasgupta, Papadimitriou, Vazirani. Algorithms, McGraw-Hill Press.
- Fotakis. Course of Discrete Mathematics at the National Technical University of Athens.
- Fotakis. Course of Algorithms and Complexity at the National Technical University of Athens.

