Lagani uvod u analizu algoritamske složenosti
Dionysis "dionyziz" Zindros <dionyziz@gmail.com>Prevod: Luka Ratic <lukaratic54@gmail.com>
- English
- Ελληνικά
- македонски
- Español
- Nederlands
- עברית
- Português
- srpskohrvatski
- Українська
- Русский
- Help translate
Uvod
Puno programera koji stoje iza jako dobrog softver, poput mnogo stvari koje viđamo na internetu ili koristimo svakodnevno, zapravo nema potpuno teorijsko znanje iz računarskih nauka. Oni su kao takvi i dalje sjajni i kreativni i zahvljaujemo im se na onome što stvaraju.
No, teorija u informatici ima svoje primene i zapravo je veoma praktična. Ovaj članak, namenjen programerima koji imaju umeće ali ne nužno i teoretsko znanje iz informatike, predstaviće jednu od najpragmatičnijih alatki računarstva: Big O notaciju ("Veliko-O") i analizu algoritamske složenosti. Kao neko ko je radio i u akademskom prostoru i na razvoju komercijalnog softvera u industriji, ovo mi je došlo kao najkorisniji alat u praksi te se nadam da ćete, po čitanju članka, razumeti kako da primenite ovo u svom kodu te ga učinite boljim. Po čitanju teksta biste trebali baratati često prisutnim programerskim žargonom i pojmovima poput velikog O (Big-O), asimptotičkog ponašanja funkcija kao i "analize najgoreg slučaja" (Worst-case analysis).
Ovaj tekst je namenjen i polaznicima srednjih škola kao, srednjoškolcima iz Grčke (kao i onima svuda drugde u Svetu) koji učestvuju na takmičenjima na međunarodnoj informatičkoj olimpijadi, takmičenju iz algoritama za studente, ili za slična takmičenja. Tekst ne zahteva neke matematičke osnove te daje solidnu podlogu za nastavak učenja o algoritmima sa razumevanjem značenja samih, kao i teorije koje stoji iza njih. Kao neko ko se takmičio pre, toplo preporučujem precizno čitanje uvodnog materijala radi potpunog razumevanja istog, jer će biti osnova za učenje algoritama kao i dalje naprednije tehnike vezane za iste.
Verujem da će ovaj tekst biti od koristi i programerima u IT industriji koji nemaju previše iskustva sa teorijom u informatici (zapravo mnogo veoma dobrih softverskih inžinjera ni nema formalno obrazovanje iz računarskih nauka). No tekst je takođe i za studente, te će ponegde zvučati i kao primeri iz udžbenika. Takođe, neke od tema u tekstu će se možda činiti kao očigledne, pogotovo ako ste se sa njima sreli tokom srednje škole. Ako ih razumete, slobodno ih zaobiđite. Neke sekcije mogu ući duboko u temu i zvučati pomalo teorijski jer studenti koji se takmiče u ovoj kategoriji trebaju biti bolje upoznati sa toeretskim osobinama algoritama od običnog praktikanta. No ove se stvari daju jako lako ispratiti i nisu gubljenje vremena. Kao što je napomenuto, tekst je namenjen srednjoškolskim učenicima te predznanje matematike nije preduslov, tako da ako vam je jasan korpus bazičnih ideja vezan za programiranje (npr. Ako znate šta je rekurzija), bićete mirni što se tiče nužnih znanja potrebnih za razumevanje teksta.
Kroz tekst ćete se susretati sa različitim vezama ka interesantnom materijalu vezanom za teme ali i malo izvan okvira onoga na šta se tekst fokusira. Ako ste programer u industriji, verovatno ćete biti upućeni u pomenute koncepte. Ako ste brucoš (polaznik studija) ili takmičar, prateći te linkove se možete dalje zainteresovati za koncepte u informatici koji vam mogu prošititi znanje vezano za tu oblast ili oblasti bliske razvoju softvera, koje niste nužno još dotakli ili istražili.
Veliko O i analiza algoritamske složenosti su nešto što se kako industrijalcima, tako i početnicima studija programiranja čini teško ili nerazumljivo, čega se neki možda boje ili odbacuju kao bespotrebno. No nije toliko teško koliko zvuči u teoriji ili kako se čini na prvu loptu. Algoritamska složenost je u biti samo formalan način merenja koliko brzo će program biti izvršen ili koliko algoritmu treba da završi, te je tako veoma pragmatičan. Počnimo uz malo motivacije.


Motivacija
Znamo već da postoje alati koji mere brzinu izvršavanja programa, poznati kao profajleri (profilers) koji mere vreme izvršavanja u milisekundama i koji nam mogu pomoći u optimizaciji koda kod uočavanja uskih grla. Iako su korisni, profajleri nemaju veze sa algoritamskom složenosti. Algoritamska složenost je koncipirana da uporedi dva algoritma na nivou ideje - ignorišući low-level detalje poput programskog jezika u kojem su implementirani, hardver koji pokreće algoritam ili arhitekturu procesora. Mi želimo da uporedimu algoritme u smislu onoga šta predstavljaju: Ideju kako nešto treba da bude izračunato. Brojanje milisekundi neće nešto puno pomoći u tom pogledu. Sasvim je moguće da loš algoritam napisan u programskom jeziku niskog nivoa kao npr. assembly bude dosta brži od algoritma iste namene koji je mnogo efikasnije napisan u programskom jeziku visokog nivoa kao što su Python ili Ruby. Stoga treba definisati značenje "boljeg algoritma".
Pošto su algoritmi programi koji izvode samo izračunavanja, ali ne i ostale stvari koje računari rade paralelno poput upravljanja mrežom ili unosom/ispisivanjem podataka, analiza složenosti nam dozvoljava da izmerimo koliko brzo program izvršava rad kada izvodi računanje odnosno komputaciju. Primeri operacija koje su isključivo računske uključuju aritmetičke operacije sa pomičnom zapetom poput sabiranja i oduzimanja, pretraga unutar baze podataka koja se nalazi u RAM-u za datu vrednost, određivanje putanje karaktera veštačke inteligencije koju mora da prođe u video-igri tako da pređe što kraći put unutar svog virtuelnog sveta (pogledati sliku 1), ili poklapanje šablona unutar teksta koristeći regularne izraze (regex, regular expression). Očigledno je da je računanje sveprisutno u programima.
Analiza složenosti je takođe alat koji nam daje način da opišemo kako se algoritam ponaša kako mu raste veličina ulaznog parametra. Ako mu damo ulazne parametre različitih veličina, kako će se algoritam onda ponašati? Ako algoritam treba 1 sekund da izvrši rad za ulaznu vrednost arbitratne veličine 1000, kako će se ponašati onda za ulaznu vrednost duplo veću od te? Hoće li mu onda trebati isto vreme, hoće li biti brži, ili četiri puta sporiji? U praktičnom programiranju, ovo je jako važno jer nam daje da predvidimo kako će se naš algoritam ponašati kada mu ulazna vrednost bude povećana. Na primer: Ako napravimo algoritam za web aplikaciju koji dobro radi sa 1000 korisnika i promerimo mu vreme izvršenja funkcije, koristeći analizu složenosti algoritma možemo stvoriti poprilično dobru sliku o tome šta će se desiti ako tu aplikaciju bude koristilo 2000 ljudi. Za takmičenja iz algoritama, analiza složenosti nam daje uvid u to koliko će se dugo naš kod izvršavati za najveće testne slučajeve date za ispitivanje tačnosti našeg algoritma. Tako da ako smo izmerili ponašanje algoritma na uzorku manje ulazne vrednosti, možemo stvoriti dobru sliku o tome kako će se taj algoritam ponašati kako mu bude rasla ulazna vrednost. Počnimo uz jednostavan primer: Nalaženje najveće vrednosti u nizu (array-u):
Brojanje instrukcija
U ovom članku, koristiću se raznim programskim jezicima u primerima. No, ne očajavajte ako niste stručni oko određenog jezika jer u koliko poznajete programiranje, možete pročitati instrukcije bez problema iako nisete upoznati sa programskim jezikom u tom primeru jer će primer biti veoma jednostavam i bez korišćenja nekih ezoteričnih funkcionalnosti. Ako ste student na takmičenjima, najverovatnije ćete koristiti C++, te nećete imati problema sa praćenjem kako se budemo kretali kroz primere. U tom slučaju preporuka je rad uz vežbe na primerima koristeći C++.
Najveći element u nizu možemo potražiti koristeći sledeći kod napisan u Javascript-u. Uzimajući u obzir niz A veličine n:
var M = A[ 0 ];
for ( var i = 0; i < n; ++i ) {
if ( A[ i ] >= M ) {
M = A[ i ];
}
}
Prvo što moramo je da izbrojimo broj osnovnih instrukcija koje izvršava ovaj kod. Ovo ćemo uraditi samo jednom i neće nam trebati za razvoj naše teorije, stoga pratite me par koraka dok ovo radimo. Kako analiziramo ovaj kod, prvo bi trebali da ga razdvojimo na jednostavne instrukcije; Stvari koje procesor može direktno da izvršava - ili nešto tome slično. Pretpostavićemo da naš procesor može da izvrši sledeće naredbe kao pojedine instrukcije:
- Dodela vrednosti promenjivoj
- Potraživanje vrednosti određenog elementa u nizu
- Upoređivanje dve vrednosti
- Uvećavanje vrednosti promenjive
- Bazične aritmetičke operacije poput sabiranja i množenja
Pretpostavićemo da se grananje (izbor između if i else delova koda posle evaluacije if kondicionala) dešava odmah i neće računati ove instrukcije. U kodu gore, prva linija je:
var M = A[ 0 ];
Ovo zahteva dve instrukcije: Jedna je potraživanje vrednosti 'A[0]' a druga je dodeljivanje vrednosti prve promenjivoj M (pretpostavljamo da je n uvek barem 1). Ove dve instrukcije su uvek potrebne algoritmu, nevezano od vrednosti n. Inicijalizacija koda for petljom takođe uvek mora da bude izvršena. Ovo nam daje još dve dodatne instrukcije, dodeljivanje i poređenje:
i = 0;
i < n;
Te instrukcije će se izvršiti pre prve iteracije for petljom. Nakon svake iteracije for petljom, potrebne su nam još dve instrukcije, dopunsko uvećavanje (inkrementacija) vrednosti i, kao i poređenje da proverimo da li ostajemo u petlji.
++i;
i < n;
Dakle, ako ignorišemo telo petlje, broj instrukcija koje algoritam traži je jednak 4+2n. To jest, 4 instrukcije na početku for petlje i 2 instrukcije na kraju svake iteracije od kojih imamo tačno n broj iteracija. Sad možemo da definišemo matematičku funkciju f(n) koja nam, za vrednost n, daje broj instrukcija potrebnih algoritmu. Za praznu for petlju, imamo f(n)=4+2n.
Analiza najgoreg slučaja (worst-case analysis)
Pogledajmo telo for petlje. Imamo operaciju potraživanja vrednosti u nizu kao i operaciju poređenja, koje se uvek sprovode.
if ( A[ i ] >= M ) { ...
To su tu dve instrukcije. Ali telo if petlje može a i ne mora da se izvrši, ovisno od toga šta su vrednosti u zadatom nizu. Ako se podesi da je A[ i ] >= M onda ćemo pokrenuti dve dodatne instrukcije -- potraživanje vrednosti u nizu i postavljanje vrednosti promenjive.
M = A[ i ]
No, sad ne možemo da definišemo f(n) tako jednostavno jer broj instrukcija ne ovisi isključivo o n, nego i o ulazu. Na primer, za A=[1, 2, 3, 4], algoritmu će trebati dodatne instrukcije nego u slučaju da je A=[4, 3, 2, 1]. Kada analiziramo algoritne, često razmatramo najgori mogući scenario. Šta je najgore šta se našem algoritmu može dogoditi? Kada naš algoritam zahteva najveći broj instrukcija? U ovom slučaju, to je kada imamo rastući niz poput A=[1, 2, 3, 4]. U tom slučaju, M treba da bude zamenjen svaki put te to daje najveći broj instrukcija. Informatičari imaju fensi naziv za to, te to zovu 'anaziza najgoreg slučaja'; To jest uzimanje u obzir najgori mogući scenario, odnosno kad baš nemamo sreće. Dakle, u najgorem mogućem slučaju, imamo 4 instrukcije koje se izvršavaju unutar tela for petlje, tako da imamo f(n)=4 + 2n + 4n = 6n + 4. Ova funkcija f, uzimajući vrednost problema veličine n, nam daje broj instrukcija potrebnih u najgorem mogućem scenariju.
Asimptotičko ponašanje funkcije
Uzimajući takvu funkciju, imamo veoma dobru ideju koliko je algoritam zapravo brz. Međutim, kako sam i obećao, nećemo morati da se mučimo sa mukotrpnim kalkulisanjem broja instrukcija u našem programu. Pored toga, stvaran broj procesorskih instrukcija potrebnih za izraz programskog jezika ovisi o kompajleru našeg programskog jezika kao i skupu instrukcija procesora (i.e. Da li se radi o AMD ili Intel Pentium-u na vašem PC-u ili je pak to MIPS na Playstation-u 2) a to smo rekli da ćemo ignorisati. Sada ćemo propustiti našu funkciju "f" kroz "filter" koji će nam pomoći da se rešimo minornih detalja koji informatičari pretenduju da ignorišu.
U našoj funkciji, 6n + 4, imamo dva izraza: 6n i 4. U analizi složenosti, jedino nam je bitno šta se događa sa funkcijom koja broji instrukcije kako raste ulazna vrednost (n). Ovo se baš slaže sa prethodnim idejama o ponašanju u "najgorem mogućem scenariju": Interesuje nas kako će se naš algoritam ponašati ako se prema njemu loše ophodimo; Kada bude izazvan da uradi nešto teško. Primećujete da je ovo vrlo korisno pri upoređuvanju algoritama. Ako jedan algoritam pretekne drugi za veću ulaznu vrednost, verovatno ostaje tačno da brži algoritam ostaje brži ako mu se zada jednostavnija, manja ulazna vrednost. Iz izraza koje razmatramo, izbacićemo sve izraze koji sporo rastu te ćemo ostaviti jedino one koji rastu brzo kako vrednost n raste. Očigledno, 4 ostaje 4 kako n raste, ali 6n raste li raste, te postaje bitniji kako se problem povećava u veličini. Stoga, prvo šta ćemo uraditi jeste da ispustimo 4 i ostavimo funkciju u obliku f(n)=6n.
Ovo ima smisla ako malo bolje razmislimo, jer 4 je samo inicijalna konstanta. Različiti programski jezici mogu varitati po vremenu koje im treba de se podese. Na primer, JAVA treba neko vreme dok inicijalizuje svoju virtuelnu mašinu (JVM - Java Virtual Machine). Kako ćemo ignorisati razlike između programskih jezika, smisleno je da ćemo ignorisati i vrednost ove konstante.
Drugo šta ćemo ignorisati je konstanta koja množi n, te naša funkcija poprima oblik f(n)=n. Kao što vidimo, ovo podosta pojednostavljuje stvari. Ponovo, ima smisla isključiti ovu konstantu množenja ako razmislimo kako se različiti programski jezici kompajluju. Pretraživanje niza u jednom jeziku će se možda drugačije kompajlovati u drugom. Primera radi: C jezik za izraz A[i] ne proverava da li je vrednost i u rasponu veličine tog niza, dok recimo Pascal to radi.
M := A[ i ]
je ekvivalent sledećem kodu u jeziku C:
if ( i >= 0 && i < n ) {
M = A[ i ];
}
Tako da je smisleno očekivati da različiti programski jezici daju različite faktore kada brojimo njihove instrukcije. U našem primeru gde koristimo "glupi kompajler" za Pascal koji je nesvestan mogućih optimizacija, Pascal traži 3 instrukcije za svaki niz umesto jedne koju traži jezik C. Izbacivanje ovog faktora se slaže sa pretpostavkom postojanja razlika između programskih jezika i kompajlera i isključive analize samog koda.
Ovaj filter "izbacivanja svih faktora" i "zadržavanja najbrže rastućeg izraza" kao što je gore opisano nazivamo asimptotičko ponašanje funkcije. Tako je asimptotično ponašanje funkcije f(n) = 2n + 8 opisano funkcijom f(n) = n. Matematički govoreći, ovde nas interesuje limit funkcije f kako n teži beskonačnosti. Ako ne razumete šta ova fraza znači formalno, bez brige, jer je ovo jedino što trebate znati. (Uzgred, u striktnom matematičkom okruženju ne bismo mogli "otkačiti" konstante do granice, ali za uslove informatike je ovo u redu prema gore definisanim razlozima). Hajde da se malo sprijateljimo da konceptom kroz par primera:
Nađimo asimptotičko ponašanje funkcije sledećih funkcija jednostavno odbacujući konstante i ostavljajući izraze koji najbrže rastu:
f( n ) = 5n + 12 daje f( n ) = n.
Koristeći istu logiku definisanu gore.
f( n ) = 109 daje f( n ) = 1.
Odbacujemo množilac 109 * 1, ali i dalje tu moramo da stavimo 1 da indikujemo da funkcija ima vrednost veću od nula.
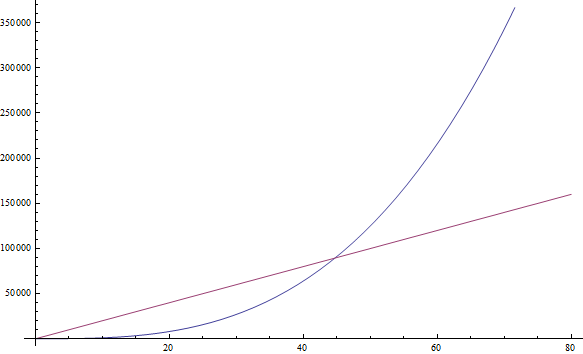
f( n ) = n2 + 3n + 112 daje f( n ) = n2
Ovde, n2 raste brže od 3n za dovoljan raspon, tako da to ostavljamo i primenjujemo prethodna pravila.
f( n ) = n3 + 1999n + 1337 daje f( n ) = n3
Iako je faktor ispred n veoma velik, idalje možemo naći n dovoljno velik tako da je n3 veći od 1999n. Kako nas interesuje ponašanje funkcije za veoma velike vrednosti n, ostavićemo jedino n3 (pogledati sliku 2).
f( n ) = n +
 daje f( n ) = n
daje f( n ) = nOvo je zato što n raste brže od korena od
 kako se povećava vrednost n n.
kako se povećava vrednost n n.
Možete sledeće probati sami:
Vežba 1
- f( n ) = n6 + 3n
- f( n ) = 2n + 12
- f( n ) = 3n + 2n
- f( n ) = nn + n
(Rezultati se nalaze dalje u tekstu)
Ako imate problem sa jednim od problema odozgo, ubacite u jednačinu neku veliku vrednost n i pogledajte koja je vrednost veća. Veoma jednostavno, zar ne?
složenost
Dakle, šta nam ovo govori, pošto smo izbacili sve dekorativne konstante, jeste da je prilično jednostavno razdvojiti asimptotičko ponašanje fukcije za brojenje instrukcija programa. Zapravo, bilo koji program koji nema ni jednu jedinu petlju će imati složenost f(n)=1, jer je broj potrebnih instrukcija zapravo samo konstanta (jedino ako ne koristi rekurziju). Bilo koji program sa jednom petljom u rasponu od 1 do n će imati f(n)=n, jer će izvršiti konstantan broj instrukcija posle petlje, kao i konstantan broj instrukcija unutar petlje koje se sve izvršavaju n puta.
Ovo bi sada trebalo biti mnogo jednostavnije i manje komplikovano za individualne instrukcije, pa hajmo pogledati par primera. Sledeći program napisan u PHP-u proverava da li određena vrednost postoji u nizu A veličine n:
<?php
$exists = false;
for ( $i = 0; $i < n; ++$i ) {
if ( $A[ $i ] == $value ) {
$exists = true;
break;
}
}
?>
Ovaj metod traženja vrednosti unutar jednog niza se zove linearna pretraga (linear search). Ovo je smisleno ime, obzirom da program ima f(n) = n (U daljem tekstu ćemo definisati šta znači linearno). Možda ćete primetiti da u kodu postoji "break" statement, koji može učiniti da program ranije okonča pa čak i posle prve iteracije. No, setimo se da tražimo najgori mogući scenario, za koji ovaj program u nizu A nema vrednost koju tražimo. Stoga je f(n) i dalje jednak n.
Vežba 2
Sistematski analizirajte broj instrukcija u gorenapomenutom PHP programu, za najgori slučaj f(n) za vrednost n, slično analizi koju smo uradili za naš prvi program u Javascript-u. Nakon toga, potvrdite da asimptotičko f(n) = n.
Pogledajmo program u Python-u za zbrajanje dva elementa u nizu, rezultat čijeg se kasnije čuva u promenjivoj:
v = a[ 0 ] + a[ 1 ]
Ovde imamo konstantan broj instrukcija, dakle f(n) = 1
Sledeći program u C++ proverava da li vektor A bilo gde u sebi (vektor je tip podataka, ukratko fensi naziv za niz) veličine n, sadrži dve iste vrednosti.
bool duplicate = false;
for ( int i = 0; i < n; ++i ) {
for ( int j = 0; j < n; ++j ) {
if ( i != j && A[ i ] == A[ j ] ) {
duplicate = true;
break;
}
}
if ( duplicate ) {
break;
}
}
Kako ovde imamo dve ugnežđene petlje jedna u drugoj, funkcija će se ponašati asimptotički prema f(n) = n2.
Praktičan savet: Jednostavni programi mogu biti analizirani i brojeći ugnežđene petlje sadržane u programu. Jedna petlja preko n članova daje f(n) = n. Petlja unutar petlje daje f(n) = n2. Petlja unutar petlje, unutar druge petlje daje f(n) = n3 i tako dalje.
Ako imamo program koji poziva funkciju unutar petlje i znamo broj instrukcija koje pozvana funkcija obavlja, možemo s lakoćom da izračunamo broj instrukcija celog programa. Pogledajmo preko ovog primera napisanog u C jeziku:
int i;
for ( i = 0; i < n; ++i ) {
f( n );
}
Ako znamo da f(n) funkcija izvršava tačno n instrukcija, možemo znati i broj instrukcija celog programa, odnosno da je to asimptotički n2, kako je funkcija pozvana tačno n puta.
Praktičan savet:Uzimajući u obzir niz sekvencijalnih for petlji, najsporija od njih određuje kako će se program ponašati asimptotički. Dve ugnežđene petlje koje prati jedna obična petlja su iste kao i te dve ugnežđene petlje same, obzirom da ugnežđene petlje preovlađuju nad jednostavnom petljom.
Pređimo sada na fensi notaciju koju informatičari koriste. Kada smo razjasnili f asimptotički, reći ćemo da je naš program Θ(f(n)). Primera radi, programi gore su vrednosti Θ(1), Θ(n2), i Θ(n2) redom. Θ(n) se izgovara "theta od n". Ponekad kažemo da f(n), originalna funkcija za brojanje instrukcija uključujući i konstante je Θ(nečega). Na primer, možemo reći da je f(n) = 2n funkcija Θ(n) -- ništa novo dakle. Takođe možemo zapisati 2n ∈ Θ(n), što izgovaramo kao "dva n je theta od n". Nemojte se zabuniti ovom notacijom jer sve što govori je da ako smo izbrojali broj instrukcija potrebnih programu i koje su 2n, onda asimptotičko ponašanje našeg algoritma opisuje n, koji smo dobili eliminišući konstante. Za dato n, sledeći matematički iskazi su tačni:
- n6 + 3n ∈ Θ( n6 )
- 2n + 12 ∈ Θ( 2n )
- 3n + 2n ∈ Θ( 3n )
- nn + n ∈ Θ( nn )
Inače, ako ste rešili prvu vežbu, upravo ovo su odgovori koje ste trebali dobiti.
Ovu funkciju, odnosno ono šta stavljamo unutar Θ( ovde ), zovemo vremenska složenost ili samo složenost našeg algoritma. Dakle algoritam sa Θ(n) ima složenost n. Takođe, radi njihove učestalosti imamo i specijalna imena za Θ(1), Θ(n), Θ(n2) i Θ(log(n)). Za Θ(1) kažemo da je algoritam konstantan ili konstantnog vremena, Θ(n) je linearan ili linearnog vremena, Θ(n2) je kvadratan ili kvadratnog vremena te Θ(log(n)) je logaritamski odnosno ima logaritamsko vreme (Ako još uvek nemate pojma šta su logaritmi, o tome ćemo malo dalje u tekstu).
Praktičan savet: Programi sa većim Θ su sporiji od programa sa manjim Θ.

Veliko O(Big-O notacija)
Ponekad je tačno da je tešto predvideti ponašanje algoritma na način koji smo gore demonstrirali, pogotovo kod kompleksnijih primera. No, možemo reći da ponašanje našeg algoritma nikad neće prekoračiti određenu granicu. Ovo nam može olakšati stvari jer nećemo morati da preciziramo tačno koliko brzo naš algoritam radi čak i kad izbacimo konstante kao što smo to ranije u radili. Ovo se lako objašnjava primerom.
Famozni problem koji informatičari koriste da studente uče algoritmima je problem sortiranja. U problemu sortiranja, niz A veličine n je dat (Zvuči poznato?) i od nas se traži da za njega napišemo program koji će ga sortirati. Problem je interesantan jer je pragmatičan u realnim sistemima. Kao na primer, File explorer treba da sortita datoteke koje prikazuje po imenu kako bi korisnik mogao da ih lakše pretražuje. Ili, drugim primerom, video igra treba da sortira 3D objekte prikazane u svetu na osnovu njihovog razmaka od igračevog oka unutar virtuelnog sveta da bi odredila šta je vidljivo a šta ne. Ovo se naziva problemom vidljivosti (Visibility Problem) (Pogledati sliku 3). Objekti koji ispadnu bliže igraču su oni koji će biti vidljivi, dok oni dalje od igrača mogu biti sakriveni iza objekata koji se nalaze ispred njih. Sortiranje je takođe interesantno jer postoji pregršt algoritama koji rešavaju ovaj problem, neki manje efikasniji od drugih. Takođe je kao problem lako definisati i objasniti poentu. Stoga, hajdemo da napišemo kod za sortiranje niza.
Evo primera neefikasnog načina za implementaciju sortiranja niza u jeziku Ruby. (Naravno, Ruby podržava sortiranje nizova pomoću postojećih pomoćnih funkcija koje bi trebalo da koristite umesto toga, i koje su svakako brže od onoga što ćemo ovde videti. Ali ovo je ovde radi ilustracije.)
b = []
n.times do
m = a[ 0 ]
mi = 0
a.each_with_index do |element, i|
if element < m
m = element
mi = i
end
end
a.delete_at( mi )
b << m
end
Ova metoda se naziva selection sort. Ona nalazi najmanji član našeg niza (Niz je definisan slovom a u primeru iznad, dok je najmanja vrednost definisana kao m, dok je mi indeks najmanje vrednosti), zatim ga stavlja na kraj novog niza (u našem slučaju je to b), i uklanja ga iz prvog niza. Zatim nalazi najmanju vrednost između preostalih vrednosti u prvom nizu, postavlja ga u novi niz koji sada broji dva elementa, te uklanja tu vrednost iz prvog niza. Ovaj proces zatim ponavlja sve dok ne izvadi poslednju vrednost u prvom nizu i prebaci je u drugi niz. Tada je niz sortiran. U ovom primeru vidimo da imamo dve ugnežđene petlje gde spoljašnja petlja radi n puta dok unutrašnja radi oniliko puta koliko ima elemenata u nizu a. Iako je dužina niza a inicijalno jednaka vrednosti n, svako ponavljanje uklanjamo jedan element iz prvobitnog niza. Tako da unutrašnja petlja "vrti" n puta na prvom koraku, zatim n-1 na drugom, n-2 na trećem i tako dalje sve do zadnje iteracije vanjske petlje gde unutrašnja petlja ima samo jednu iteraciju.
Malo je teže evaluirati složenost ovog programa obzirom da moramo da izračunamo sumu 1 + 2+ ... + (n-1) + n. No zasigurno mu možemo naći gornju granicu. Tako da možemo da promenimo naš program (to u glavi, ne u pravom kodu) tako da ga učinimo sporijim od prvobitnog pa onda izračunamo složenost novog programa. Ako možemo naći složenost lošijeg programa kog smo napisali, onda znamo da je naš originalni program najviše toliko loš, ili bolji. Tako ako nađemo da je složenost novog programa dosta dobra, koja je isto i lošija od one prvobitnog programa, možemo računati da će i naš originalni program imati solidnu složenost - ili dobru koliko i onaj sporiji koji smo napravili, ili bolje od toga.
Sad, razmislimo malo kako možemo da promenimo ovaj program iz primera da mu dođemo do složenosti. No, imajmo na umu da možemo samo da ga pogoršamo (napravimo takvog da ima veći broj instrukcija) tako da je naša procena značajna za originalni program. Očigledno možemo da promenimo unutrašnju petlju da se uvek vrti tačno n puta umesto da ta vrednost varira. Neka od tih ponavljanja će možda biti beskorisna, no pomoći će nam da analiziramo složenost rezultirajućeg algoritma. Ako ga jednostavno promenimo, onda je novi algoritam jasno Θ(n2), jer imamo dve ugnežđene petlje koje se obe ponavljaju tačno n puta. Ako je takom onda kažemo da je originalni algoritam O(n2). O(n2) se izgovara kao "O od n na kvadrat". Šta ovo znači jeste da je naš program asimptotičko ništa gori od n2. Možda je bolji od toga, ili je možda identičan toj vrednosti. Uzgred, ako je naš program zaista složenosti Θ(n2), i dalje možemo reći da je O(n2). Da si pomognete da bi razumeli šta to znači, zamislite da promenite originalni program na način da ga ne menja puno ali i dalje ga malo pogorša u pogledu složenosti time što mu doda beznačajnu instrukciju na početak programa. Time će pomeriti proces brojanja instrukcija za jednustavnu konstantu koja je odbačena kada je u pitanju asimptotičko ponašanje funkcije. Dakle, program koji je Θ(n2) je isto i O(n2).
Ali program koji ima O(n2) nema nužno i Θ(n2). Na primer, bilo koji program koji ima Θ(n) takođe ima i O(n2) i pored toga što ima O(n). Ako zamislimo da je Θ(n) program jednostavna for petlja koja se ponavlja n puta, možemo je učiniti gorom time što ćemo je smestiti u obgrljujuću for petlju koja se takođe ponavlja n puta time proizvodeći program koji ima f(n)=n2. Generalizacije radi, bilo koji program koji ima Θ(a) je i O(b) ako je b gore od a. Primetićete i da promene na našem programu ne daju program koji je nužno smislen ili ekvivalentan originalnom. Jedino što treba je da izvršava više instrukcija od originala za datu n. Sve za šta ga koristimo je brojanje instrukcija, ne nužno rešavanje problema.
Dakle, reći da naš program ima O(n2) je sigurno: Analizirali smo algoritam, i pronašli smo da ni u jednom slučaju nije gori od n2. Ali može biti da i zapravo je n2. Ovo nam daje dobru procenu koliko brzo naš program radi. Prođimo kroz par primera da se upoznamo da novom notacijom.
Vežba 3
Naći šta je od sledećeg tačno:
- Algoritam koji ima Θ(n) ima i O(n)
- Algoritam koji ima Θ(n) ima i O(n)
- Algoritam koji ima Θ(n2) ima i O(n3)
- Algoritam koji ima Θ(n) ima i O(1)
- Algoritam koji ima O(1) ima i Θ(1)
- Algoritam koji ima O(n) ima i Θ(1)
Rešenje
- Znamo da je ovo tačno jer je naš originalni program imao Θ(n). Možemo dostići O(n) i bez da promenimo naš program.
- Kako je n2 gore od n, ovo je tačno.
- Kako je n3 gore od n2, ovo je tačno.
- Kako 1 nije gore od n, ovo nije tačno. Ako program ima n instrukcija asimptotičko (linearni broj instrukcija), ne možemo ga učiniti gorim i da pored toga asimptotički ima samo 1 instrukciju (konstantan broj instrukcija).
- Ovo je tačko jer su dve složenosti iste.
- Ovo može i ne mora biti tačno, ovisno od algoritma. U opštem slučaju je netačno. Ako algoritam ima Θ(1), onda ima sigurno i O(n), ali ako je O(n) onda ne može onda ne može imati Θ(1). Kao primer, Algoritam sa Θ(n) ima O(n) ali ne i Θ(1).
Vežba 4
Koristeći zbir aritmetičkog niza, dokazati da program odozgo nije samo O(n2) već i Θ(n2). Ako ne znate šta je aritmetički niz, pogledajte ovde, u suštini je veoma jednostavno.
Zbog toga što O-složenost algoritma daje gornju granicu za složenost algoritma, dok Θ daje stvarnu složenost algoritma, kažemo da nekada Θ daje "usku granicu". Ako znamo da smo dobili granicu složenosti algoritma koja nije "uska", onda možemo iskoristiti i malo O (o) da to označimo. Na primer, ako algoritam ima Θ(n), onda je granična verdnost O(n) uska. Ali vrednost za O(n2) nije uska, te tako možemo da napišemo da je algoritam o(n2), što se izgovara kao "malo o od n na kvadrat", da pokaže da granica nije uska. Bolje je ako možemo pronaći uske granične vrednosti za naše algoritme, jer iste daju bolju informaciju o tome kako se algoritam ponaša no isto nije uvek jednostavno.
Vežba 5
Pronaći koje su granične vrednosti uske i koje nisu. Proveriti da li je neka od vrenosti netačna. Koristiti o "malo o" da bi predstavili da granice nisu uskete.
- Algoritam koji ima Θ(n) ima i gornju granicu O(n).
- Algoritam koji ima Θ(n2) ima i gornju granicu O(n3).
- Algoritam koji ima Θ(1) ima i gornju granicu O(n).
- Algoritan koji ima Θ(n) ima i gornju granicu O(1).
- Algoritam koji ima Θ(n) ima i gornju granicu O(2n)
Rešenje
- U ovom slučaju, Θ složenost i O složenost su iste, te je granica uska.
- Ovde vidimo da je O složenost veće razmere od Θ složenosti te ova granica nije uska. Granica O(n2) bi zaista bila uska. Tako možemo napisati da je algoritam o(n3).
- Ponovo vidimo da je O složenost veće razmere od Θ složenosti dakle imamo granicu koja nije uska. Tako možemo napisati da O(n) granična vrednost nije uska te je označiti sa o(n).
- Ovde mora da je počinjena greška da računanjem granice, obzirom da je netačna. Nemoguće je da je algoritam sa Θ(n) sa gornjom granicom od O(1), kako je n veće složenosti od 1. Zapamtite da O daje gornju granicu.
- Ovo možda liči na granicu koja nije uska no, zapravo je obrnuto. Setite se da je asimptotičko ponašanje kod 2n i n isti, i da O i Θ brinu samo za asimptotičko ponašanje. Tako da imamo O(2n) = O(n) te je ova granica uska kako je složenost ista kao i za Θ.
Praktičan savet: Jednostavnije je otkriti O-složenost algoritma nego njegovu Θ-složenost.
Možda ste sada malo preplavljeni svim ovim notacijama, no uvedimo još dva dodatna simbola pre nego što nastavimo na još primera. Jednostavni su obzirom da smo razjasnili Θ, O i o (malo O), te ih nećemo puno koristiti u daljem tekstu, no korisno je znati ih čim smo već tu. U primeru gore, modifikovali smo naš program da bi ga učinili gorim (tj. povećali mu broj instrukcija i sa time i vreme računanja) te smo našli O notaciju. O ovde ima značaj jer nam govori da naš program neće imati učinak gori od specifične granice, pa nam daje važne informacije da bi jamčili da je program dovoljno dobar. Ako uradimo suprotno, i poboljšamo rad našeg programa te proizvedemo iz toga složenost rezultujućeg programa, koristićemo noraciju Ω. Omega (Ω) notacija nam dakle daje složenost za koju znamo da je u tom slučaju najoptimalnija moguća. Ovo je korisno ako želimo da dokažemo da je algoritam prespor ili loš u određenom slučaju. Na primer, recimo da algoritam ima Ω(n3), što znači da u najboljem mogućem slučaju algoritam ne može bolje od n3. Može biti i Θ(n3), ili čak Θ(n4), ili čak gore ali znamo da je barem na nekoj razini neefikasan. Dakle Ω označava donju granicu za složenost našeg algoritma. Slično o (malo O), možemo koristiti i ω ako znamo da naša granica nije uska. Na primer, algoritam koji ima Θ(n3) ima o(n4), i ω(n2). Ω(n) se izgovara kao "Veliko omega od n", dok je ω "malo omega od n".
Vežba 6
Za sledeće složenosti Θ, naći usku i ne-usku O granicu kao, kao i iste za Ω po izboru, pod uslovom da su moguće.
- Θ( 1 )
- Θ(
 )
) - Θ( n )
- Θ( n2 )
- Θ( n3 )
Rešenje
Ovo je poprilično jednostavna primena gore definisanih pravila
- Uska granica će biti O(1) kao i Ω(1). Ne-uska granica za O je O(n). Podsetimo se da O daje gornju granicu. Kako je n veće razmere od 1 ovo je ne-uska granica te je takođe možemo zapisati kao o(n). Ali ne možemo naći i ne-uskuu granicu za Ω jer ne možemo ići niže of 1 za ovakve funkcije te ćemo se morati zadovoljiti uskom granicom.
- Uske granice će biti iste kao i Θ te će biti O(
 ) i Ω(
) i Ω(  ) po redu. Za ne-uske granice imamo da je O(n), kako je n veće od
) po redu. Za ne-uske granice imamo da je O(n), kako je n veće od  , te je tako gornja granica za
, te je tako gornja granica za  .
Kako znamo da je ovo ne-uska gornja granica, možemo je zapisati i kao o(n). Za donju granicu koja nije uska, možemo reći da je Ω(1). Kako znamo da ova granica nije uska, možemo je predstaviti i kao ω(1).
.
Kako znamo da je ovo ne-uska gornja granica, možemo je zapisati i kao o(n). Za donju granicu koja nije uska, možemo reći da je Ω(1). Kako znamo da ova granica nije uska, možemo je predstaviti i kao ω(1). - Uske granice su O(n) i Ω(n). Dve ne-uske granice mogu biti ω(1) i o(n3). Ove su zapravo veoma loše predstavljene kao granice, ali su daleko od izvornih složenosti, tako da rade posao za potrebe naše definicije.
- Uske granice su O(n32) i Ω(n2). Za ne-uske granice možemo koristiti ω(1) i o(n3) iz prethodnog primera.
- Uske granice su O( n3 ) i Ω( n3 ) redom. Dve ne-uske granice mogu biti ω(
 n2 ) i o(
n2 ) i o(  n3 ). Iako ove granice nisu uske, bolje su od onih odozgo.
n3 ). Iako ove granice nisu uske, bolje su od onih odozgo.
Razlog zašto koristimo O i Ω umesto Θ iako O i Ω takođe mogu da nam daju uske granice jeste što možda nećemo moći odrediti je li granica koju smo našli uska ili možda samo ne želimo da mnogo ispitujemo.
Ako niste u potpunosti zapamtili sve simbole i njihova značenja, ne brinite sad mnogo jer se uvek možete vratiti natrag i proveriti. Najbitniji simboli su O i Θ.
Takođe je bitno napomenuti da iako Ω daje ponašanje u donjem graničnom opsegu za našu funkciju (tj. popravili smo naš program te on sad ima manji broj instrukcija), i dalje mislimo na analizu najgoreg slučaja. To je zato što računaru dajemo najgore moguće ulazne parametre za dato n te analiziramo njegovo ponašanje pod ovom pretpostavkom.
Sledeća tabela ukazuje na simbole koje smo upravo uveli i njihovu ekvivalente sa uobičajenim matematičkim simbolima poređenja koje koristimo za brojeve. Razlog zašto ovde ne koristimo uobičajene simbole i umesto njih koristimo grčka slova je da istaknemo da radimo asimptotičko poređenje ponašanja, a ne samo jednostavno poređenje.
| Asimptotički operator poređenja | Numerički operator poređenja |
|---|---|
| Naš algoritam je o( nečega ) | Broj je < nečega |
| Naš algoritam je O( nečega ) | Broj je ≤ nečega |
| Naš algoritam je Θ( nečega ) | Broj je = nečega |
| Naš algoritam je Ω( nečega ) | Broj je ≥ nečega |
| Naš algoritam je ω( nečega ) | Broj je > nečega |
Praktičan savet: Iako su svi simboli O, o, Ω, ω i Θ u biti korisni, O (veliko o) je najčešće korišćeno jer ga je lakše izvesti od Θ i praktičnije je od Ω.
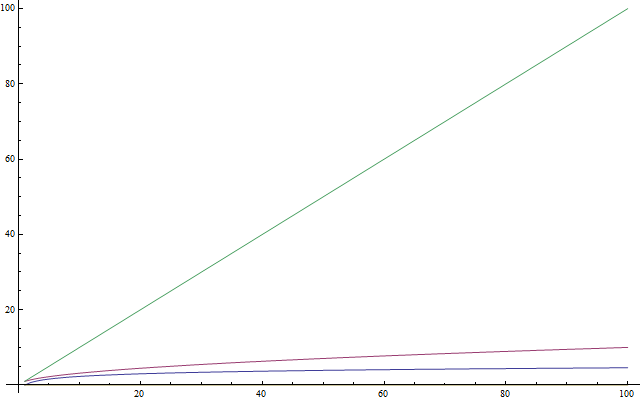
Logaritmi
Ako znate šta su logaritmi, slobodno preskočite ovo. Kako mnogo ljudi ne razume logaritme, ili ih nisu mnogo koristili u zadnje vreme i ne sećaju ih se, ova sekcija je korisna za podsetiti se. Ovo je korisno i za malđe studente koji se još nisu susreli sa logaritmima. Logaritmi su važni jer mnogo puta iskaču pri analizi složenosti. Logaritam je operacija primenjena na broj tako da ga dosta smanji - poput kvadratnog korena nekog broja. Tako da, ako postoji nešto što treba izvući iz lekcije o logaritmima, to je da uzmu broj i umanje ga u odnosu na original (pogledati sliku 4). Na isti način na koji su kvadratni koreni inverzne operacije kvadriranju, logaritmi su inverzne operacije stepenovanju. Nije toliko komplikovano koliko zvuči. Bolje je objašnjeno primerom. Uzmimo u obzir jednačinu:
2x = 1024
Želimo da rešimo jednačinu za x. Zapitamo se: Na koji broj treba dići 2 da bismo dobili 1024? Odgovor je 10. Jer, ako imamo 210 dobijamo 1024, što je lako proveriti. Logaritmi nam pomažu da opišemo ovaj problem koristeći novi izraz. U ovom slučaju, 10 je logaritam broja 1024, i to zapisujemo kao log(1024), te čitamo kao "Logaritam od 1024". Zato jer koristimo 2 kao bazu, ove logaritme nazivamo logaritmi sa bazom 2. Postoje i logaritmi sa drugim bazama, no u ovom tekstu ćemo koristiti isključivo logaritme sa bazom odnosno osnovom 2. Ako ste student na međunarodnim takmičenjima, topla preporuka je obnoviti malo logaritme nakon što ovo pročitate. U informatici, logaritmi sa bazom 2 su mnogo češći od ostalih, primarno iz razloga što često imamo samo dva različita entiteta: 0 i 1. Takođe naginjemo ka tome da probleme prepolovimo na dva dela, tim pre su logaritmi sa osnovom 2 ono što jedino treba znati za u nastavku teksta.
Vežba 7
Rešite dole navedene jednačine. Označite koji logaritam nalazite u svakom slučaju. Koristite samo logaritamsku osnovu 2.
- 2x = 64
- (22)x = 64
- 4x = 4
- 2x = 1
- 2x + 2x = 32
- (2x) * (2x) = 64
Solution
Ovde nema mnogo pametovanja, samo treba primeniti koncepte koje smo gore definisali.
- Kroz malo isprobavanja različitih vrednosti možemo utvrditi da x = 6, te je log(64) = 6
- Ovde primećujemo da se (22)x, prema svojstvima eksponenata, može zapisati kao 22x. Dakle, imamo da je 2x = 6 jer je log( 64 ) = 6 iz prethodnog rezultata i stoga je x = 3.
- Koristeći znanje iz prethodne jednačine, možemo zapisati 4 kao 22 i tako naša jednačina postaje (22)x = 4 što je isto kao i 22x = 4. Tada primećujemo da je log( 4 ) = 2 jer je 22 = 4 i stoga imamo da je 2x = 2. Dakle, x = 1. Ovo se lako može primetiti iz originalne jednačine, jer korišćenje eksponenta od 1 kao rezultat daje bazu.
- Setimo se da je eksponent 0 daje 1. Tako imamo log( 1 ) = 0 jer je 20 = 1, te je x = 0.
- Ovde imamo zbir i ne možemo direktno naći logaritam. Međutim, primećujemo da je 2x + 2x isto što i 2 * (2x). Dakle, pomnožili smo u još dva, i stoga je ovo isto kao 2x + 1 i sada sve što treba da uradimo je da rešimo jednačinu 2x + 1 = 32. Nalazimo da je log( 32 ) = 5 i tako x + 1 = 5 i stoga je x = 4.
- Množimo zajedno dva stepena od 2, pa ih možemo spojiti tako što ćemo primetiti da je (2x) * (2x) isto što i 22x. Tada sve što treba da uradimo je da rešimo jednačinu 22x = 64 koju smo već rešili gore i tako je x = 3.
Praktičan savet: Za algoritme koje pišete na takmičenjima implementirane u C++, nakon što analizirate njihovu složenost, možete dobiti grubu procenu koliko će brzo vaš program raditi tako što ćete očekivati da će izvršiti oko 1.000.000 operacija u sekundi, pri čemu su operacije koje brojite date asimptotičkim ponašanjem funkcija koja opisuje vaš algoritam. Na primer, algoritmu θ( n ) potrebno je oko sekunde da obradi ulaz za n = 1.000.000.
Složenost rekurzije
Sada imamo slučaj rekurzivne funkcije. Rekurzivna funkcija je funkcija koja samu sebe poziva. Možemo li analizirati ovu složenost? Iduća funkcija izračunava faktorijel datog broja. Faktorijel broja se dobija množenjem tog broja sa svim prethodnim pozitivnim celim brojevima. Na primer, faktorijel 5 je 5 * 4 * 3 * 2 * 1 što zapisujemo kao "5!" i izgovaramo kao "faktorijel od 5", no neki ljudi to vole da izgovaraju samo vrišteći: "PET!!!"
def factorial( n ):
if n == 1:
return 1
return n * factorial( n - 1 )
Hajde da izanaliziramo složenost ove funkcije. Funkcija nema petlje ali njena složenost nije ni konstantna. Da bi utvrdili složenost funkcije moramo da se vratimo na brojanje instrukcija. Jasno je da ako funkciji prosledimo argument n, ona će se izvršiti n puta. Ako niste sigurni šta ovo znači, pokušajte ručno i da n = 5 da potvrdimo da ovo ima smisla. Na primer, ako je n = 5, funkcija će se pokrenuti 5 puta, i kako će se n smanjivati za 1 u svakom pozivu funkcije. Time vidimo da ova funkcija ima složenost Θ(n).
Ako i dalje niste sigurni oko ovoga, pokušajte da se setite da uvek možete naći tačnu složenost računajući ručno broj instrukcija. Ako želite, pokušajte sad da izbrojite broj instrukcija izvedenih u ovoj funkciji da nađete f(n) i dokažete da je zaista linearna (setimo se da linearno znači Θ(n)).
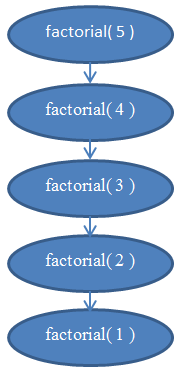
Pogledajte sliku 5 za dijagram koji vam može pomoći da razumete rekurzije izvedene kad je funkcina factorial(5) pozvana.
Ovo bi trebalo da razjasni zašto funkcija ima linearnu složenost.
Logaritamska složenost
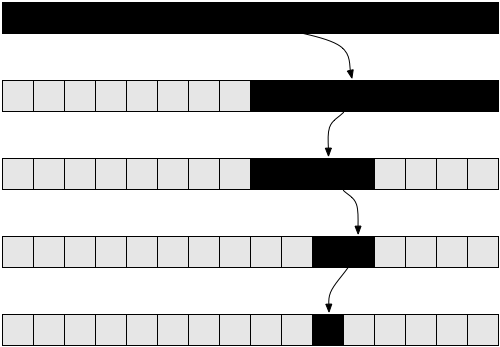
Jedan famozan problem u informatici je pronalaženje elementa u nizu. Ovo smo ranije rešili u za opšti oblik. Ovaj problem postaje interesantniji ako imamo niz koji već dolazi sortiran a u kome mi trebamo da pronađemo određenu vrednost. Jedan način da se ovo izvede je preko binarne pretrage (binary search). Prvo krenemo od srednjeg elementa u nizu: Ako smo ga tu našli, gotovi smo! U suprotnom, ako je vrednost koja se tu nalazi veća od one koju tražimo, znamo da se naš element nalazi u levoj polovini niza. Ako je vrednost veća, onda tražimo u desnoj polovini. Nastavljamo da prepolovljavamo niz sve dok na kraju ne ostane jedan element koji će se ili se neće podudarati. Ovo je implementacija algoritma u pseudokodu:
def binarySearch( A, n, value ):
if n = 1:
if A[ 0 ] = value:
return true
else:
return false
if value < A[ n / 2 ]:
return binarySearch( A[ 0...( n / 2 - 1 ) ], n / 2 - 1, value )
else if value > A[ n / 2 ]:
return binarySearch( A[ ( n / 2 + 1 )...n ], n / 2 - 1, value )
else:
return true
Ovaj pseudokod je pojednostavljivanje implementacije. U praksi, ovaj metod je lakše opisati nego implementirati, kako programer mora da se pobrine oko par problema koji mogu da iskrsnu u implementaciji. Tu su tzv. off-by-one ili OBOE ili OBO greške te deljenje dvojkom možda neće uvek proizvesti ceolobrojnu vrednost te je potrebno upotrebiti floor() i ceil() funkcije na dobijenoj vrednosti. No, za naše potrebe možemo da pretpostavimo da će uvek raditi i da će naša implementacije rešiti i off-by-one greške kako samo želimo da analiziramo složenost ove metode. Ako nikad do sada niste implementirali binarnu pretragu, možda biste mogli da probate u programskom jeziku po želji.
Pogledajte sliku 6 da bi bolje razumeli kako funkcioniše binarna pretraga.
Ako niste sigurni da ovaj metod zaista funkcioniše, odvojite trenutak da ga pokrenete ručno na jednostavnom primeru i uverite se da zaista radi.
Pokušajmo sada da analizirano ovaj algoritam. Ponovo imamo rekurzivni algoritam. Pretpostavimo, jednostavnosti radi, da je niz uvek podeljen na pola ignorišući momentalno +1 i -1 u rekurziji. Dosad bi trebalo da bude jasno da se ignorisanjem -1 i +1 ne menja rezultat složenosti. Ovo je činjenica koju bi normalno trebali da dokazujemo ako bismo hteli da budemo obazrivi iz matematičke tačke gledišta, no praktično je to jasno po intuiciji. Pretpostavimo da nam je niz tačno stepen dvojke, radi pojednostavljivanja. Opet ovakve asumpcije ne menjaju krajnje rezultate složenosti koje trebamo da dobijemo. Najgori slučaj u ovom slučaju bi bio kada u nizu koji ispitujemo ne bi posojala vrednost koju tražimo. U tom slučaju počinjemo sa nizom veličine n u prvom koraku rekurzije, pa se spuštamo na niz veličine n/a, pa zatim n/4, n/8 i tako dalje. Generalno se naš niz deli svakog stepena rekurzije na pola, dok ne dođemo do 1. Dakle, hajde da izvedemo broj elemenata za svaki stepen rekurzije:
Primećujemo kako u i-toj iteraciji naš niz ima n/21 elemenata. Razlog ovome je što se kod svake iteracije niz smanjuje na pola svoje dužine, što znači da se broj elemenata deli na dva. Oso se prevodi u množenje imenioca (denominatora) sa 2. Ako to uradimo i puta, dobićemo n/2i. Ova procedura se nastavlja te za svako veće i dobijamo manji broj elemenata dok ne dođemo do poslednje iteracije gde nam ostaje samo 1 element. Ako želimo da saznamo vrednost i da bi videli za koju iteraciju bi se to desilo, moramo rešiti sledeće:
1 = n / 2i
Ovo će biti tačno samo u slučaju kada dođemo do poslednjeg koraka funkcije binarySearch(), ne i u opštem slučaju. Rešenje za i će nam pomoći da nađemo u kojoj iteraciji će se rekurzija zaustaviti. Množeći obe strane sa 21 dobijamo:
2i = n
Ova jednačina bi trebala da izgleda poznato ako ste pročitali sekciju sa logaritmima odozgo. Rešavaući i, imamo da je:
i = log( n )
Ovo nam govori da je broj iteracija potrebnih za izvođenje binarne pretrage log(n) gde je n broj elemenata u originalnom nizu.
Ako malo razmislimo, ovo ima smisla. Na primer, uzmimo da je n = 32, dakle niz od 32 elementa. Koliko puta moramo da ga prepolovimo da dođemo do jednog elementa? Pa imaćemo: 32 → 16 → 8 → 4 → 2 → 1. Dakle, ovo smo uradili 5 puta, što je logaritam od 32. Time je složenost binarne pretrage lednaka Θ( log(n) ).
Ovaj zadnji rezultat nam daje da uporedimo binarnu i linearnu pretragu koju smo prethodno razmotrili. Jasno je da je log(n) manja vrednost od n te je razumno zaključiti da je binarna pretraga mnogo brža metoda pretraživanja niza od linearne pretrage stoga bi bilo pametno sortirati nizove radi efikasnije pretrage.
Praktično pravilo: Poboljšanje asimptotičkog vremena rada programa često značajno povećava njegove performanse, mnogo više od bilo koje manje „tehničke“ optimizacije kao što je korišćenje bržeg programskog jezika.
Optimalno sortiranje
Čestitke! Sada ste naučili kako analizirati algoritamsku složenost, asimptotičko ponašanje funkcija kao i o Big-O notaciji. Takođe sada znati kako da intuitivno zaključite je li složenost algoritma O(1), O(log(n)), O(n), O(n2) i tako dalje. Poznajete simbole o, O, ω, Ω i Θ i znate šta znači analiza najgoreg slučaja (worst-case analysis). Ako ste do ovde dogurali, ovaj tutorijal je poslužio svrsi.
Ova finalna sekcija je po izboru. Malo je komplikovanija pa je možete slobodno preskočiti ako vam se čini kao previše. Sledeći deo teksta će tražiti više pažnje i detaljnije razmatranje primera, no zato će vam zati znanje o veoma korisnim metodama iz analize algoritamske složenosti, stoga su vredne pokušaja razumevanja.
Gore smo prošli kroz implementaciju selektivnog sortiranja. Pomenuli smo da se selection sort ne smatra optimalnim. Optimalni algoritam je algoritam koji problem rešava na najbolji mogući način, što znači da nema boljih algoritama od takvog, odnosno da svi ostali algoritmi koji pokušavaju rešiti isti problem imaju makar istu ili goru složenost. Možda postoje i različiti algoritmi koji dele isti nivo složenosti. Problem sortiranja se optimalno može rešiti na različite načine. Možemo iskoristiti iste ideje iz binarne pretrage za brzo sortiranje. Ovakav metod se zove mergesort ili sortiranje spajanjem.
Za izvođenje mergesort algoritma, prvo moramo proizvesti pomoćnu funkciju koja će doći u korist kada budemo vršili sortiranje. Napravićemo merge funkciju koja uzima dva već sortirana niza i spaja ih u jedan niz. Ovo je lako urađeno kroz:
def merge( A, B ):
if empty( A ):
return B
if empty( B ):
return A
if A[ 0 ] < B[ 0 ]:
return concat( A[ 0 ], merge( A[ 1...A_n ], B ) )
else:
return concat( B[ 0 ], merge( A, B[ 1...B_n ] ) )
Concat ili funkcija za spajanje (konkatenaciju) uzima stavku, "head" ili "glavu", i niz, "tail" odnosno "rep" i proizvodi i vraća novi niz sa glavom kao prvim elementom kao i ostalim elementima koji predstavlja ostale elemente u nizu. Na primer, concat(3, [4, 5, 6]) vraća [3, 4, 5, 6]. Koristimo A_n i B_n da bi označili veličine za niz A i B.
Vežba 8
Proveriti da li funkcija gore zaista izvršava spajanje. Napišite funkciju u svom preferiranom programskom jeziku koristeći iteraciju (for petlje) umesto rekurzije.
Analiza ovog algoritma otkriva da ima vreme rada Θ( n ), gde je n dužina rezultujućeg niza (n = A_n + B_n).
Vežba 9
Proveriti da li je Θ(n) vreme rada za merge.
Koristeći ovu funkciju možemo stvoriti bolji algoritam za sortiranje. Ideja je sledeća: podelimo niz na dva dela. Svaki od dva dela sortiramo rekurzivno, a zatim spajamo dva sortirana niza u jedan veliki niz. U pseudokodu to izgleda ovako:
def mergeSort( A, n ):
if n = 1:
return A # it is already sorted
middle = floor( n / 2 )
leftHalf = A[ 1...middle ]
rightHalf = A[ ( middle + 1 )...n ]
return merge( mergeSort( leftHalf, middle ), mergeSort( rightHalf, n - middle ) )
Ova funkcija je komplikovanija za razumeti od onoga što smo bili obišli, pa bi sledeća vežba mogla da potraje par minuta.
Vežba 10
Proveriti ispravnost funkcije mergeSort. To jest, proveriti da li funkcija mergeSort vrši radnju kojom je definisana odnosno da li sortira dati niz. Ako imate problem da razumete zašto funkcija radi to što radi, pokušajte je pokrenuti ručno na primeru kratkog niza. Kada pokrećete funkciju, uverite se da su leftHalf i rightHalf (leva i desna polovina niza) zapravo proizvod otprilike na pola presečenog niza. Ne mora biti precizno u sredini ako se desi da niz ima neparan broj elemenata (zato je u kodu iznad upotrebljena funkcija floor)
Kao finalni primer, analiziraćemo složenost mergeSort funkcije. Za svaki korak mergeSort funkcije, podelićemo niz na dva jednaka dela, kao kod binarne pretrage (binarySearch). No u ovom slučaju zadržavamo obe polovine kroz izvršavanje programa. Potom primenjujemo algoritam rekurzivno za svaku polovinu. Pošto rekurzija izbaci povratnu vrednost, primenjujemo merge operaciju na rezultate što traži Θ(n) vremena.
Dakle, delimo originalni niz na pola veličine n/2 svake. Nakon toga, spajamo te nizove, što je operacija koja spaja n elemenata stoga traje Θ(n) vremena.
Pogledajmo sliku 7 da bismo razumeli rekurziju.
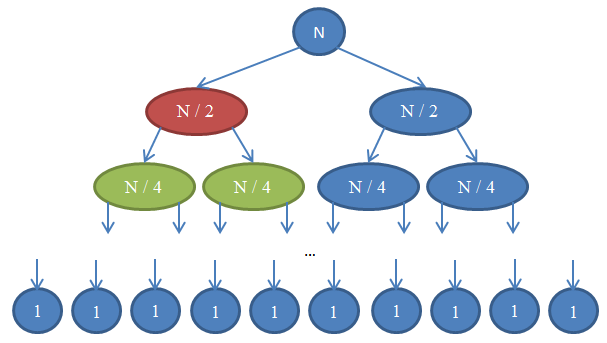
Pogledajmo šta se ovde događa. Svaki krug predstavlja poziv funkciji mergeSort. Broj upisan u krugu predstavlja veličinu niza koji je skladišten. Plavi krug na vrhu je inicijalni poziv funkciji mergeSort, gde sortiramo niz veličine n. Strelice indikuju kasnije rekurzivne pozive funkcije. Inicijalni poziv funkcije mergeSort dvaput poziva tu funkciju za dva niza, svaki niz veličine n/2. Ovo je indikovano strelicama na vrhu. Zauzvrat, svaki od ovih poziva funkcije ponovo dvaput za sebe poziva funkciju mergeSort za dva niza veličina n/4 svaki, i tako sve dok ne dođemo do niza veličine 1. Ovaj dijagram se zove stablo rekurzije (recursion tree), jer ilustruje kako se rekurzija ponaša i izgleda kod strukture stabla (gde je koren na vrhu a lišće na dnu, što je realno izvrnuto stablo).
Primećujemo i da za svaki red u dijagramu iznad, ukupan broj elemenata je jednak n. Da bi ovo videli, pogledajte svaki red ponaosob. Prvi red ima samo jedan poziv funkciji mergeSort sa nizom veličine n, te je ukupan broj elemenata n. Drugi red ima dva poziva funkciji mergeSort, svaki veličine n / 2. Pošto su n/2 + n/2 = n, i u ovom redu je ukupan broj elemenata jednak n. U trećem redu imamo 4 invokacije mergeSort funkcije za niz veličine n/4, koji proizvodi ukupan broj elemenata veličine n/4 + n/4 + n/4 + n/4 = 4n/4 = n. Tako da ponovo imamo n elemenata. Primećujemo da i za svaki red u dijagramu, pozivalac mora da izvrši i merge radnju nad dobijenim elementima. Na primer, crveni krug mora da sortira n/2 elemenata. Da bi to uradila, ona podeli niz veličine n/2 na dva veličine n/4 pozivajući za svaki funkciju mergeSort rekurzivno da bi ih sortirala (ti pozivi su zeleni kružići), te ih onda spaja (merge). Ova funkcija traži da spaja elemente n/2. Za svaki red stabla, ukupan broj spojenih elemenata je n. U redu koji smo upravo posetili, naša funkcija spaja n/2 elemente a funkcija desno od nje mora da spoji svojih n/2 elemenata. To nam daje n elemenata u totalu koji moraju da se spoje u redu u kojem se nalazimo.
Prema ovom argumentu, složenost za svaki red je Θ(n). Znamo da će broj redova u ovom dijagramu, koji se takođe naziva dubinom stabla rekurzije, biti log(n). Obrazloženje za ovo je potpuno isto kao i ono koje smo koristili kada smo analizirali složenost binarnog pretraživanja. Imamo log(n) redova i svaki je Θ(n), stoga je složenost mergeSort funkcije Θ(n * log(n)). Ovo je mnogo bolje od Θ(n2) što nam je dalo sortiranje selekcije (zapamtite da je log(n) mnogo manji od n, pa je n * log( n ) mnogo manji od n * n = n2). Ako vam ovo zvuči komplikovano, ne brinite: nije uvek lako na prvu loptu. Vratite se ponovo kada malo razbistrite misli i pročitajte ponovo o argumentima kada budete implementirali mergeSort u svom programskom jeziku po želji i potvrdite da algoritam radi.
Kao što ste videli u zadnjem primeru, analiza složenosti nam pomaže da uporedimo algoritme da bi videli koji radi bolje. Pod tim okolnostima, možemo biti prilično sigurni da će sortiranje spajanjem nadmašiti sortiranje selekcijom za velike nizove. Ovaj zaključak bi bilo teško izvesti da nemamo teoretsku podlogu iz analize algoritama koju smo razvili. U praksi, svakako su algoritmi za sortiranje sa vremenom rada Θ(n * log(n)) oni u upotrebi. Na primer, Linuxov kernel koristi heapsort algoritam za sortiranje, koji ima isto vreme rada kao i mergesort (Dakle Θ(n log( n )), što je optimalno), koji smo ovde izanalizirali. Primećujete da nismo dokazali da su algoritmi koje smo koristili zaista efikasni. To bi zahtevalo malo detaljniji matematički postupak, no budite sigurni da ne mogu biti gori u pogledu složenosti.
Pošto ste završili sa čitanjem ovo tutorijala, intuiciju za analizu složenosti algoritama koju ste razvili bi vam trebala pomoći u dizajniranju bržih programa i fokusiranju na optimizaciju veoma bitnih stvari u kodu u odnosu na one stvari koje su trivijalne, time dajući mogućnost da budete produktivniji. Dodatno, matematički jezik i žargon poput Big-O notacije koji ste izvukli iz teksta vam može dobro pomoći u komuniciranju sa ostalim softverskim inženjerima onda kada biste hteli da povedete raspravu o vremenu rada algoritama što ćete uskoro zaista moći i da uradite sa novostečenim znanjem.
O ovome
Ovaj članak je licenciran pod Creative Commons 3.0 Attribution licencom. To znači da možete da ga kopirate i lepite, delite, objavite na sajt, izmenite i radite šta god vam padne napamet, uz to da umetnete moje ime. Iako to ne morate, ako bazirate svoj rad na mom, podstičem vas da svoje tekstove objavljujete pod Creative Commons licencom tako da su isti lakši za deljenje i saradnju. Isto tako, moram da navedem izvore koje sam koristio. Ove kul ikonice na stranici se zovu fugue icons. Lea Verou je autorka prugastog dizajna. Takođe, bitnije of svega, algoritme, bez kojih ne bih mogao ovo da napišem, su me podučili profesori Nikos Papaspyrou i Dimitris Fotakis.
Trenutno radim na odbrani doktorata na temu kriptografije na univerzitetu u Atini. Tokom pisanja ovog članka sam bio na dodiplomskom iz elektrotehnike i računarstva na Nacionalnom Tehničkom institutu u Atini baveći se softverom, te sam bio trener na Grčkom takmičenju iz informatike. Što se tiče industrije, bio sam deo tima inžinjera koji su stvorili deviantART, društvenu mrežu za umetnike, deo tima sigurnosti u Twitter-u i Google-u, kao i deo startapa Zino i Kamibu gde smo se bavili društvenim mrežama i razvojem video igara, redom. Možete me pratiti na twitter-u, ili na github-u ako ste u ovome uživali, ili mi poslati email ako želite da stupimo u kontakt. Mnogi mladi programeri nemaju dobro znanje engleskog, stoga mi možete poslati email ako biste preveli tekst na svoj maternji jezik kako bi više ljudi moglo da ga pročita.
Hvala na čitanju! Na pisanju ovog teksta nisam zaradio, tako da ako vam se ovo svidelo, slobodno mi prosledite email pozdrave. Uživam da dobijam slike mesta oko Sveta, tako da slobodno ako imate, zakačite neku svoju fotku u vašem gradu.
Reference
- Cormen, Leiserson, Rivest, Stein. Introduction to Algorithms, MIT Press.
- Dasgupta, Papadimitriou, Vazirani. Algorithms, McGraw-Hill Press.
- Fotakis. Course of Discrete Mathematics at the National Technical University of Athens.
- Fotakis. Course of Algorithms and Complexity at the National Technical University of Athens.

