Μια Εύπεπτη Εισαγωγή στην Ανάλυση Πολυπλοκότητας Αλγορίθμων
Διονύσης "dionyziz" Ζήνδρος <dionyziz@gmail.com>- English
- Ελληνικά
- македонски
- Español
- Nederlands
- עברית
- Português
- srpskohrvatski
- Українська
- Русский
- Help translate
Εισαγωγή
Πολλοί προγραμματιστές που φτιάχνουν κάποια από τα καλύτερα και πιο χρήσιμα προγράμματα σήμερα, όπως πολλά από τα πράγματα που βλέπουμε στο διαδίκτυο και χρησιμοποιούμε καθημερινά, δεν έχουν υπόβαθρο στη θεωρητική επιστήμη των υπολογιστών. Είναι, παρ' όλα αυτά τρομερά ικανοί και δημιουργικοί προγραμματιστές και τους ευχαριστούμε για όσα κατασκευάζουν.
Παρ' όλα αυτά, η θεωρητική επιστήμη των υπολογιστών έχει τις χρήσεις και τις εφαρμογές της και μπορεί να γίνει αρκετά πρακτική. Σε αυτό το άρθρο, που απευθύνεται σε προγραμματιστές που γνωρίζουν την τέχνη τους αλλά δεν έχουν υπόβαθρο στη θεωρητική επιστήμη των υπολογιστών, παρουσιάζω ένα από τα πιο πρακτικά εργαλεία της επιστήμης των υπολογιστών: το συμβολισμό big O και την ανάλυση πολυπλοκότητας αλγορίθμων. Ως κάποιος που έχει δουλέψει τόσο σε ένα ακαδημαϊκό περιβάλλον επιστήμης των υπολογιστών όσο και στην κατασκευή λογισμικού production ποιότητας στη βιομηχανία, αυτό είναι το εργαλείο που μου έχει φανεί ένα από τα πραγματικά χρήσιμα στην πράξη, οπότε ελπίζω ότι μετά την ανάγνωση αυτού του άρθρου θα μπορείτε να το εφαρμόσετε στον κώδικά σας για να τον κάνετε καλύτερο. Αφού διαβάσετε αυτό το άρθρο, θα μπορείτε να καταλαβαίνετε όλους τους συνήθεις όρους που χρησιμοποιούν οι επιστήμονες των υπολογιστών όπως "big O", "ασυμπτωτική συμπεριφορά" και "ανάλυση χειρότερης περίπτωσης".
Αυτό το κείμενο απευθύνεται επίσης σε μαθητές γυμνασίου και λυκείου από την Ελλάδα ή από οπουδήποτε αλλού παγκοσμίως που αγωνίζονται στην Παγκόσμια Ολυμπιάδα Πληροφορικής, έναν αλγοριθμικό διαγωνισμό για μαθητές, ή άλλους παρόμοιους διαγωνισμούς όπως ο Πανελλήνιος Διαγωνισμός Πληροφορικής. Έτσι, δεν έχει προαπαιτούμενες γνώσεις μαθηματικών και θα σας παρέχει το υπόβαθρο που χρειάζεστε για να συνεχίσετε τις σπουδές σας στους αλγορίθμους έχοντας μία βαθύτερη κατανόηση της θεωρίας που βρίσκεται από πίσω. Ως κάποιος που διαγωνιζόταν σε τέτοιους μαθητικούς διαγωνισμούς, σας συμβουλεύω να διαβάσετε όλο αυτό το εισαγωγικό υλικό και να προσπαθήσετε να το καταλάβετε πλήρως, διότι θα είναι απαραίτητο καθώς μελετάτε αλγορίθμους και μαθαίνετε πιο προχωρημένες τεχνικές.
Πιστεύω ότι αυτό το κείμενο θα είναι βοηθητικό για προγραμματιστές στη βιομηχανία που δεν έχουν μεγάλη εμπειρία στη θεωρητική επιστήμη των υπολογιστών (είναι γεγονός ότι κάποιοι από τους πιο εμπνευσμένους μηχανικούς λογισμικού δεν έχουν πάει ποτέ στο πανεπιστήμιο). Αλλά επειδή είναι ταυτόχρονα και για μαθητές, μπορεί μερικές φορές να ακούγεται σαν σχολικό κείμενο. Επιπρόσθετα, μερικά από τα ζητήματα σε αυτό το κείμενο μπορεί να φαίνονται υπερβολικά προφανή· για παράδειγμα, μπορείτε να τα έχετε δει στα σχολικά σας χρόνια. Αν νιώθετε ότι τα καταλαβαίνετε, μπορείτε να τα προσπεράσετε. Άλλες ενότητες μπαίνουν σε λίγο μεγαλύτερο βάθος και γίνονται ελαφρώς θεωρητικές, καθώς οι μαθητές που διαγωνίζονται σ' αυτό το διαγωνισμό χρειάζεται να ξέρουν περισσότερα περί θεωρίας αλγορίθμων από το μέσο επαγγελματία. Αλλά αυτά τα πράγματα είναι επίσης καλό να τα ξέρετε και δεν είναι τρομερά δύσκολο να τα παρακολουθήσετε, οπότε είναι πιθανότατα μία πολύ καλή επένδυση του χρόνου σας. Καθώς το αρχικό κείμενο απευθυνόταν σε μαθητές γυμνασίου και λυκείου, δεν χρειάζεται μαθηματικό υπόβαθρο, οπότε οποιοσδήποτε έχει κάποια εμπειρία στο να προγραμματίζει (π.χ. αν ξέρετε τι είναι αναδρομή) θα μπορεί να παρακολουθήσει χωρίς κανένα πρόβλημα.
Διάσπαρτα σε τούτο το άρθρο θα βρείτε διάφορα links προς ενδιαφέρον υλικό συχνά εκτός του εύρους στο οποίο συζητιέται το εν λόγω θέμα στο παρόν άρθρο. Αν είστε προγραμματιστής που δουλεύει στη βιομηχανία, είναι πιθανό να είστε εξοικειωμένος με το μεγαλύτερο μέρος αυτών των εννοιών. Αν είστε μαθητής γυμνασίου ή λυκείου που συμμετέχει σε διαγωνισμούς, ακολουθώντας αυτούς τους συνδέσμους θα βρείτε ενδείξεις για άλλες περιοχές της επιστήμης των υπολογιστών ή του τομέα των μηχανικών λογισμικού που ενδέχεται να μην έχετε εξερευνήσει και που μπορείτε να κοιτάξετε για να διευρύνετε τα ενδιαφέροντά σας.
Ο συμβολισμός big O και η ανάλυση πολυπλοκότητας αλγορίθμων είναι κάτι που τόσο πολλοί προγραμματιστές στη βιομηχανία όσο και μαθητές βρίσκουν δύσκολο να κατανοήσουν, φοβούνται, ή αποφεύγουν θεωρώντας το ως άχρηστο. Όμως δεν είναι όσο δύσκολο ή όσο θεωρητικό όσο φαίνεται εκ πρώτης όψεως. Η αλγοριθμική πολυπλοκότητα είναι απλώς ένας τρόπος να μετρήσουμε πόσο γρήγορα τρέχει ένα πρόγραμμα ή ένας αλγόριθμος, οπότε είναι κάτι πραγματικά αρκετά πρακτικό. Ας ξεκινήσουμε δίνοντας μερικά κίνητρα για τη μελέτη του θέματος.

Κίνητρα
Ξέρουμε ήδη ότι υπάρχουν εργαλεία για να μετρήσουμε πόσο γρήγορα τρέχει ένα πρόγραμμα. Υπάρχουν προγράμματα που λέγονται profilers τα οποία μετρούν το χρόνο εκτέλεσης σε milliseconds και μας βοηθούν να βελτιστοποιούμε τον κώδικά μας εντοπίζοντας τα bottlenecks. Μολονότι αυτό είναι ένα χρήσιμο εργαλείο, δεν σχετίζεται στην πραγματικότητα με την πολυπλοκότητα αλγορίθμων. Η πολυπλοκότητα αλγορίθμων είναι κάτι σχεδιασμένο για να συγκρίνει δύο αλγορίθμους στο επίπεδο της ιδέας — αγνοώντας λεπτομέρειες χαμηλού επιπέδου όπως η γλώσσα προγραμματισμού υλοποίησης, το υλικό πάνω στο οποίο τρέχει ο αλγόριθμος, ή το σύνολο εντολών του επεξεργαστή. Θέλουμε να συγκρίνουμε αλγορίθμους ακριβώς γι' αυτό που είναι: Ιδέες για το πώς κάτι υπολογίζεται. Το να μετράμε milliseconds δε μας βοηθά σ' αυτό. Είναι αρκετά πιθανό ένας κακός αλγόριθμος γραμμένος σε μία γλώσσα χαμηλού επιπέδου όπως η assembly να τρέχει πολύ πιο γρήγορα απ' ό,τι ένας καλός αλγόριθμος υλοποιημένος σε μία γλώσσα υψηλού επιπέδου όπως η Python ή η Ruby. Ήρθε, λοιπόν, η ώρα να ορίσουμε τι είναι πραγματικά ένας "καλύτερος αλγόριθμος".
Καθώς οι αλγόριθμοι είναι προγράμματα που πραγματοποιούν έναν υπολογισμό, και όχι άλλα συνήθη πράγματα με τα οποία καταπιάνονται οι υπολογιστές όπως εργασίες δικτύου ή είσοδος και έξοδος προς το χρήστη, η ανάλυση πολυπλοκότητας μας επιτρέπει να μετρήσουμε πόσο γρήγορο είναι ένα πρόγραμμα όταν εκτελεί υπολογισμούς. Παραδείγματα διαδικασιών που είναι καθαρά υπολογιστικές περιλαμβάνουν αριθμητικές πράξεις κινητής υποδιαστολής όπως η πρόσθεση κι ο πολλαπλασιασμός· η αναζήτηση σε μία βάση δεδομένων που χωράει στη μνήμη για μία δεδομένη τιμή· ο προσδιορισμός της διαδρομής που θα ακολουθήσει ένας χαρακτήρας τεχνητής νοημοσύνης σε ένα βιντεοπαιχνίδι έτσι ώστε να χρειάζεται να περπατήσει μόνο μικρή απόσταση μέσα στον εικονικό κόσμο (βλ. Εικόνα 1)· ή η εκτέλεση μίας κανονικής έκφρασης για να ελέγξουμε αν ταιριάζει σε κάποιο αλφαριθμητικό. Ξεκάθαρα, ο υπολογισμός είναι πανταχού παρών στα προγράμματα υπολογιστών.
Η ανάλυση πολυπλοκότητας είναι επίσης ένα εργαλείο που μας επιτρέπει να εξηγήσουμε πώς ένας αλγόριθμος συμπεριφέρεται καθώς η είσοδος μεγαλώνει. Αν του δώσουμε διαφορετική είσοδο, πώς θα συμπεριφερθεί ο αλγόριθμός; Αν ο αλγόριθμός μας χρειάζεται 1 δευτερόλεπτο για να τρέξει σε είσοδο με μέγεθος 1000, πώς θα συμπεριφερθεί αν διπλασιάσω το μέγεθος της εισόδου; Θα τρέξει το ίδιο γρήγορα, με τη μισή ταχύτητα, ή τέσσερις φορές πιο αργά; Στον προγραμματισμό στην πράξη, αυτό είναι σημαντικό καθώς μας επιτρέπει να προβλέψουμε πώς ο αλγόριθμός μας θα συμπεριφερθεί καθώς η είσοδος μεγαλώνει. Για παράδειγμα, αν έχουμε φτιάξει έναν αλγόριθμο για μία εφαρμογή στο web που δουλεύει καλά με 1000 χρήστες και μετρήσουμε το χρόνο εκτέλεσής του, χρησιμοποιώντας ανάλυση πολυπλοκότητας αλγορίθμων μπορούμε να έχουμε μια αρκετά καλή ιδέα για το τι θα συμβεί μόλις φτάσουμε τους 2000 χρήστες. Για τους αλγοριθμικούς διαγωνισμούς, η ανάλυση πολυπλοκότητας μάς πληροφορεί για το πόσο χρόνο θα κάνει ο κώδικάς μας να τρέξει για τα μεγαλύτερα testcases που θα χρησιμοποιηθούν για να ελέγξουν την ορθότητα του προγράμματός μας. Οπότε αν έχουμε μετρήσει τη συμπεριφορά του προγράμματός μας για μικρή είσοδο, μπορούμε να έχουμε μία καλή ιδέα για το πώς θα συμπεριφερθεί για μεγαλύτερη είσοδο. Ας ξεκινήσουμε με ένα απλό παράδειγμα: Την εύρεση του μεγίστου στοιχείου ενός πίνακα.
Μετρώντας εντολές
Σε αυτό το άρθρο θα χρησιμοποιήσω ποικίλες γλώσσες προγραμματισμού στα παραδείγματα. Όμως μην απελπίζεστε αν δεν ξέρετε μία συγκεκριμένη γλώσσα προγραμματισμού. Καθώς ξέρετε προγραμματισμό, θα μπορείτε να διαβάζετε τα παραδείγματα χωρίς κανένα πρόβλημα ακόμα και αν δεν είστε εξοικειωμένος με τη γλώσσα προγραμματισμού της επιλογής μου, καθώς θα είναι απλά και δεν θα χρησιμοποιώ καμία από τις μυστήριες λειτουργίες της εκάστοτε γλώσσας. Αν είστε μαθητής και διαγωνίζεστε σε αλγοριθμικούς διαγωνισμούς, σχεδόν σίγουρα δουλεύετε με την C++, οπότε δεν θα έχετε πρόβλημα να παρακολουθήσετε. Σ' αυτή την περίπτωση, σας συνιστώ να λύσετε τις ασκήσεις χρησιμοποιώντας C++ για εξάσκηση.
Το μέγιστο στοιχείο σ' ένα πίνακα μπορεί να βρεθεί χρησιμοποιώντας ένα απλό τμήμα κώδικα όπως αυτό το κομμάτι κώδικα Javascript. Δεδομένης εισόδου ενός πίνακα A μεγέθους n:
var M = A[ 0 ];
for ( var i = 0; i < n; ++i ) {
if ( A[ i ] >= M ) {
M = A[ i ];
}
}
Τώρα, το πρώτο πράγμα που θα κάνουμε είναι να μετρήσουμε πόσες βασικές εντολές εκτελεί αυτό το τμήμα κώδικα. Αυτό θα το κάνουμε μόνο μία φορά και δεν θα είναι απαραίτητο καθώς αναπτύσσουμε τη θεωρία μας, οπότε κάντε υπομονή μερικά λεπτά όσο ασχολούμαστε με δαύτο. Καθώς αναλύουμε αυτό το τμήμα κώδικα, θέλουμε να το σπάσουμε σε απλές εντολές· πράγματα που μπορούν να εκτελεστούν από τον επεξεργαστή άμεσα - ή κάτι κοντά σ' αυτό. Θα υποθέσουμε ότι ο επεξεργαστής μας μπορεί να εκτελέσει το καθένα από τα ακόλουθα ως μία εντολή:
- Την ανάθεση μιας τιμής σε κάποια μεταβλητή
- Την εύρεση της τιμής ενός συγκεκριμένου στοιχείου σ' ένα πίνακα
- Τη σύγκριση δύο τιμών
- Την αύξηση κάποια τιμής
- Τις βασικές αριθμητικές πράξεις όπως η πρόσθεση κι ο πολλαπλασιασμός
Θα υποθέσουμε ότι η διακλάδωση (η επιλογή ανάμεσα στα τμήματα κώδικα if και else αφότου υπολογιστεί η συνθήκη του if) γίνεται στιγμιαία και δε θα μετρήσουμε αυτές τις εντολές. Στον παραπάνω κώδικα, η πρώτη γραμμή είναι:
var M = A[ 0 ];
Αυτό απαιτεί 2 εντολές: Μία για την εύρεση του A[ 0 ] και μία για την ανάθεση της τιμής στο M (υποθέτουμε ότι το n είναι πάντα τουλάχιστον 1). Αυτές οι δύο πράξεις χρειάζονται πάντα από τον αλγόριθμο. Ο κώδικας αρχικοποίησης του for πρέπει επίσης να τρέξει πάντα. Αυτό μας δίνει δύο επιπλέον εντολές· μία ανάθεση και μία σύγκριση:
i = 0;
i < n;
Αυτές θα τρέξουν πριν την πρώτη επανάληψη του for. Μετά από κάθε επανάληψη του for, χρειάζεται να τρέξουμε δύο επιπλέον εντολές, μία αύξηση του i και μία σύγκριση για να δούμε αν θα παραμείνουμε μέσα στο βρόγχο:
++i;
i < n;
Συνεπώς, αν αγνοήσουμε το σώμα του βρόγχου, ο αριθμός των εντολών που χρειάζεται αυτός ο αλγόριθμος είναι 4 + 2n. Δηλαδή 4 εντολές στην αρχή του for και 2 εντολές στο τέλος κάθε επανάληψης εκ των οποίων έχουμε n. Μπορούμε τώρα να ορίσουμε μία μαθηματική συνάρτηση f( n ) που, δοθέντος ενός n, μας δίνει τον αριθμό των εντολών που χρειάζεται ο αλγόριθμος. Για ένα for με άδειο σώμα, έχουμε f( n ) = 4 + 2n.
Ανάλυση χειρότερης περίπτωσης
Τώρα, κοιτάζοντας το σώμα του for, έχουμε μία εντολή εύρεσης στοιχείου πίνακα και μία σύγκριση που λαμβάνουν χώρα πάντοτε:
if ( A[ i ] >= M ) { ...
Αυτές είναι δύο εντολές από μόνες τους. Όμως το σώμα του if μπορεί να τρέξει ή μπορεί και όχι, ανάλογα με το τι τιμές έχει πραγματικά ο πίνακας. Αν συμβεί και είναι A[ i ] >= M, τότε θα τρέξουμε αυτές τις δύο επιπλέον εντολές — μία εύρεση στοιχείου πίνακα και μία ανάθεση:
M = A[ i ]
Όμως τώρα δεν μπορούμε να ορίσουμε μία f( n ) τόσο εύκολα, επειδή ο αριθμός των εντολών δεν εξαρτάται αποκλειστικά από το n αλλά και από την είσοδο. Για παράδειγμα, για A = [ 1, 2, 3, 4 ] ο αλγόριθμος θα χρειαστεί περισσότερες εντολές απ' ό,τι για A = [ 4, 3, 2, 1 ]. Όταν αναλύουμε αλγόριθμους, συχνά λαμβάνουμε υπ' όψιν τη χειρότερη περίπτωση. Ποιο είναι το χειρότερο πράγμα που μπορεί να συμβεί στον αλγόριθμό μας; Πότε χρειάζεται ο αλγόριθμός μας τις περισσότερες εντολές για να ολοκληρωθεί; Στην περίπτωσή μας, αυτό συμβαίνει όταν έχουμε έναν πίνακα με στοιχεία σε αύξουσα σειρά όπως το A = [ 1, 2, 3, 4 ]. Σ' αυτή την περίπτωση, το M πρέπει να αντικαθίσταται κάθε φορά και έτσι αυτό οδηγεί στο μέγιστο αριθμό εντολών. Οι επιστήμονες των υπολογιστών έχουν ένα φανταχτερό όνομα γι' αυτό και το λένε ανάλυση χειρότερης περίπτωσης ή worst-case analysis· αυτό δεν είναι τίποτ' άλλο από απλώς να λαμβάνουμε υπ' όψιν την περίπτωση που είμαστε πιο άτυχοι. Άρα, στη χειρότερη περίπτωση, έχουμε 4 εντολές να τρέξουμε μέσα στο σώμα του for, οπότε έχουμε f( n ) = 4 + 2n + 4n = 6n + 4. Αυτή η συνάρτηση f, δεδομένου του μεγέθους του προβλήματος n, μας δίνει τον αριθμό των εντολών που θα χρειαζόμασταν στη χειρότερη περίπτωση.
Ασυμπτωτική συμπεριφορά
Έχοντας μία τέτοια συνάρτηση, έχουμε μία αρκετά καλή ιδέα για το πόσο γρήγορος είναι ο αλγόριθμός μας. Όμως, όπως υποσχέθηκα, δεν θα χρειάζεται να περνάμε από την επίπονη διαδικασία του να μετράμε εντολές στο πρόγραμμά μας. Εξάλλου, ο αριθμός των πραγματικών εντολών του επεξεργαστή που χρειάζονται για κάθε εντολή σε κάθε γλώσσα προγραμματισμού εξαρτάται από το μεταγλωττιστή της γλώσσας προγραμματισμού μας και το σύνολο διαθέσιμων εντολών επεξεργαστή (π.χ. αν είναι ένας AMD ή ένας Intel Pentium στο PC σας ή ένας επεξεργαστής MIPS στο Playstation 2 σας) και είπαμε ότι κάτι τέτοιο θα το αγνοήσουμε. Θα περάσουμε τώρα τη συνάρτηση "f" μέσα από ένα "φίλτρο" το οποίο θα μας βοηθήσει να ξεφορτωθούμε αυτές τις μικρές λεπτομέρειες που οι επιστήμονες των υπολογιστών προτιμούν να αγνοούν.
Στη συνάρτησή μας, 6n + 4, έχουμε δύο όρους: το 6n και το 4. Στη ανάλυση πολυπλοκότητας μάς ενδιαφέρει μόνο τι συμβαίνει στη συνάρτηση μέτρησης εντολών όσο η είσοδος του προγράμματος (n) μεγαλώνει. Αυτό στην πραγματικότητα ταιριάζει με τις προηγούμενες ιδέες της συμπεριφοράς "στη χειρότερη περίπτωση": Μας ενδιαφέρει πώς ο αλγόριθμός μας συμπεριφέρεται όταν τον κακομεταχειριζόμαστε· όταν τον προκαλούμε με κάτι δύσκολο. Σημειώστε ότι αυτό είναι πραγματικά χρήσιμο όταν συγκρίνουμε αλγορίθμους. Αν ένας αλγόριθμος νικά έναν άλλο για μεγάλη είσοδο, τότε κατά πάσα πιθανότητα ο γρηγορότερος αλγόριθμος παραμένει γρηγορότερος όταν του δώσουμε μία ευκολότερη, μικρότερη είσοδο. Από τους όρους που λαμβάνουμε υπ᾽ όψιν, θα πετάξουμε όλους εκείνους τους όρους που μεγαλώνουν αργά και θα κρατήσουμε μόνο εκείνους τους όρους που μεγαλώνουν γρήγορα όσο το n μεγαλώνει. Ξεκάθαρα το 4 παραμένει 4 όσο το n μεγαλώνει, όμως το 6n συνεχίζει να αυξάνεται, οπότε τείνει να παίζει όλο και μεγαλύτερο ρόλο για μεγαλύτερα προβλήματα. Συνεπώς, το πρώτο πράγμα που θα κάνουμε είναι να πετάξουμε το 4 και να μας μείνει η συνάρτηση f( n ) = 6n.
Αυτό βγάζει νόημα αν το σκεφτείτε, καθώς το 4 είναι απλώς μία "σταθερά αρχικοποίησης". Διαφορετικές γλώσσες προγραμματισμού μπορεί να έχουν διαφορετικές απαιτήσεις χρόνου για να ξεκινήσουν να τρέχουν. Για παράδειγμα, η Java χρειάζεται κάποιο χρόνο για να αρχικοποιήσει την εικονική της μηχανή. Καθώς αγνοούμε τις διαφορές στο επίπεδο των γλωσσών προγραμματισμού, δεν είναι παρά λογικό το να αγνοήσουμε αυτή την τιμή.
Το δεύτερο πράγμα που θα αγνοήσουμε είναι η πολλαπλασιαστική σταθερά μπροστά από το n, κι έτσι η συνάρτησή μας θα γίνει f( n ) = n. Όπως βλέπετε, τούτο απλοποιεί πολύ τα πράγματα. Και πάλι, βγάζει νόημα το ότι πετάμε αυτή τη σταθερά αν σκεφτούμε με ποιον τρόπο οι διαφορετικές γλώσσες προγραμματισμού μεταγλωττίζονται. Η πράξη της "εύρεσης στοιχείου πίνακα" μπορεί να μεταγλωττίζεται σε διαφορετικές εντολές σε διαφορετικές γλώσσες προγραμματισμού. Για παράδειγμα, στη C, όταν κάνουμε A[ i ] η γλώσσα δεν ελέγχει ότι το i είναι εντός των δηλωμένων ορίων του πίνακα, ενώ στην Pascal αυτός ο έλεγχος γίνεται. Συνεπώς, ο ακόλουθος κώδικας σε Pascal:
M := A[ i ]
είναι ισοδύναμος με τον ακόλουθο κώδικα σε C:
if ( i >= 0 && i < n ) {
M = A[ i ];
}
Οπότε είναι λογικό να περιμένουμε ότι οι διαφορετικές γλώσσες προγραμματισμού θα οδηγήσουν σε διαφορετικούς συντελεστές όταν μετράμε τις εντολές τους. Στο παράδειγμά μας όπου χρησιμοποιούμε έναν χαζό μεταγλωττιστή για την Pascal ο οποίος δεν ξέρει τίποτα για πιθανές βελτιστοποιήσεις, η Pascal χρειάζεται 3 εντολές για κάθε πρόσβαση σε στοιχείο πίνακα αντί για τη 1 εντολή που χρειάζεται η C. Το ότι πετάμε αυτό το συντελεστή είναι συμβατό με την ιδέα ότι αγνοούμε τις διαφορές ανάμεσα σε συγκεκριμένες γλώσσες προγραμματισμού και μεταγλωττιστές και αναλύουμε μόνο την ιδέα του ίδιου του αλγορίθμου.
Αυτό το φίλτρο της "απόρριψης όλων των συντελεστών" και της "διατήρησης μόνο του όρου που μεγαλώνει πιο γρήγορα" όπως περιγράφεται παραπάνω είναι αυτό που λέμε ασυμπτωτική συμπεριφορά. Άρα η ασυμπτωτική συμπεριφορά του f( n ) = 2n + 8 περιγράφεται από τη συνάρτηση f( n ) = n. Από μαθηματικής σκοπιάς, αυτό που λέμε εδώ είναι ότι μας ενδιαφέρει το όριο της συνάρτησης f καθώς το n τείνει στο άπειρο· όμως αν δεν καταλαβαίνετε τι σημαίνει αυτή η φράση σε φορμαλιστικό επίπεδο, μη σας νοιάζει, καθώς αυτό είναι το μόνο που χρειάζεται να ξέρετε. (Σαν παρατήρηση, σε ένα αυστηρό μαθηματικό περιβάλλον, δεν θα μπορούσαμε να πετάξουμε απλώς τις πολλαπλασιαστικές σταθερές στο όριο· όμως για τις χρήσεις της επιστήμης των υπολογιστών, θέλουμε να μπορούμε να κάνουμε κάτι τέτοιο για τους λόγους που περιγράφονται παραπάνω.) Ας δουλέψουμε πάνω σε μερικά παραδείγματα για να εξοικειωθούμε με την ιδέα.
Ας βρούμε την ασυμπτωτική συμπεριφορά των συναρτήσεων στα ακόλουθα παραδείγματα διαγράφοντας τους σταθερούς συντελεστές και κρατώντας τους όρους που μεγαλώνουν γρηγορότερα.
Η f( n ) = 5n + 12 δίνει f( n ) = n.
Χρησιμοποιώντας ακριβώς την ίδια λογική με παραπάνω.
Η f( n ) = 109 δίνει f( n ) = 1.
Πετάμε τον πολλαπλασιαστή 109 * 1, αλλά χρειάζεται να κρατήσουμε το 1 εδώ πέρα ώστε να δείξουμε ότι αυτή η συνάρτηση έχει μη μηδενική τιμή.
Η f( n ) = n2 + 3n + 112 δίνει f( n ) = n2
Εδώ, η n2 μεγαλώνει γρηγορότερα από την 3n για αρκετά μεγάλα n, οπότε αυτό θα κρατήσουμε.
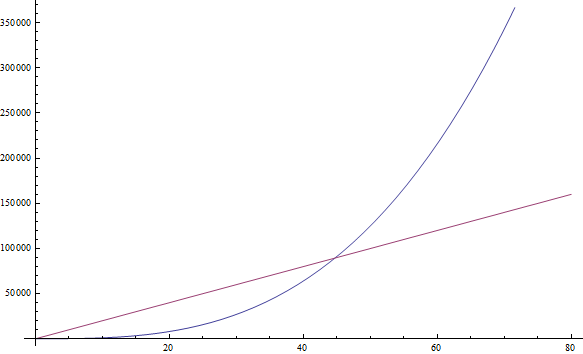
Η f( n ) = n3 + 1999n + 1337 δίνει f( n ) = n3
Παρ᾽ όλο που ο συντελεστής μπροστά από το n είναι μεγάλος, μπορούμε να βρούμε ένα αρκετά μεγάλο n τέτοιο ώστε το n3 να γίνει μεγαλύτερο του 1999n. Καθώς μας ενδιαφέρει η συμπεριφορά για πολύ μεγάλες τιμές του n, κρατάμε μόνο το n3 (βλ. Εικόνα 2).
Η f( n ) = n +
 δίνει f( n ) = n
δίνει f( n ) = nΤούτο προκύπτει διότι το n μεγαλώνει γρηγορότερα από το
 καθώς αυξάνουμε το n.
καθώς αυξάνουμε το n.
Μπορείτε να δοκιμάσετε τα παρακάτω παραδείγματα μόνος σας:
Άσκηση 1
- f( n ) = n6 + 3n
- f( n ) = 2n + 12
- f( n ) = 3n + 2n
- f( n ) = nn + n
(Σημειώστε τα αποτελέσματά σας· η λύση δίνεται πιο κάτω)
Αν αντιμετωπίζετε πρόβλημα με κάποιο από τα παραπάνω, αντικαταστήστε για κάποια μεγάλη τιμή του n και δείτε ποιος όρος μεγαλώνει γρηγορότερα. Αρκετά εύκολο, δε βρίσκετε;
Πολυπλοκότητα
Άρα αυτό που μας μένει είναι ότι καθώς μπορούμε να πετάξουμε όλες αυτές τις διακοσμητικές σταθερές, είναι αρκετά εύκολο το να βρούμε την ασυμπτωτική συμπεριφορά της συνάρτησης μέτρησης εντολών ενός προγράμματος. Στην πραγματικότητα, οποιοδήποτε πρόγραμμα δεν περιέχει βρόγχους θα έχει f( n ) = 1, καθώς ο αριθμός των εντολών που χρειάζεται είναι απλώς μία σταθερά (εκτός αν χρησιμοποιεί αναδρομή· βλ. παρακάτω). Οποιοδήποτε πρόγραμμα έχει μόνο ένα βρόγχο που πάει από το 1 έως το n θα έχει f( n ) = n, καθώς θα τρέχει ένα σταθερό πλήθος εντολών πριν το βρόγχο, ένα σταθερό πλήθος εντολών μετά το βρόγχο, και ένα σταθερό πλήθος εντολών μέσα στο βρόγχο κάθε μία από τις οποίες τρέχει n φορές.
Αυτό θα πρέπει να είναι αρκετά πιο εύκολο και λιγότερο επίπονο από τη μέτρηση εντολών μία-μία, οπότε ας ρίξουμε μια ματιά σε μερικά παραδείγματα για να εξοικειωθούμε. Το παρακάτω πρόγραμμα σε PHP ελέγχει αν μία συγκεκριμένη τιμή υπάρχει μέσα σε ένα πίνακα A μεγέθους n:
<?php
$exists = false;
for ( $i = 0; $i < n; ++$i ) {
if ( $A[ $i ] == $value ) {
$exists = true;
break;
}
}
?>
Αυτή η μέθοδος αναζήτησης μίας τιμής μέσα σε ένα πίνακα λέγεται γραμμική αναζήτηση. Αυτό είναι ένα λογικό όνομα, αφού αυτό το πρόγραμμα έχει f( n ) = n (θα ορίσουμε ακριβώς τι σημαίνει "γραμμικός" στην επόμενη ενότητα). Μπορεί να παρατηρήσατε ότι υπάρχει μία εντολή "break" εδώ η οποία μπορεί να κάνει το πρόγραμμα να τερματίσει νωρίτερα, ακόμη και μετά από μία μόνο επανάληψη. Όμως θυμηθείτε ότι ενδιαφερόμαστε για το σενάριο της χειρότερης περίπτωσης, που γι᾽ αυτό το πρόγραμμα συμβαίνει όταν ο πίνακας A δεν περιέχει την τιμή. Οπότε συνεχίζουμε να έχουμε f( n ) = n.
Άσκηση 2
Αναλύστε συστηματικά το πλήθος των εντολών που χρειάζεται το παραπάνω PHP πρόγραμμα ως προς το n στη χειρότερη περίπτωση και βρείτε το f( n ), με τον ίδιο τρόπο που αναλύσαμε το πρώτο μας πρόγραμμα σε Javascript. Στη συνέχεια επιβεβαιώστε ότι, ασυμπτωτικά, έχουμε f( n ) = n.
Ας δούμε ένα πρόγραμμα σε Python το οποίο προσθέτει δύο στοιχεία ενός πίνακα μαζί και στη συνέχεια αποθηκεύει αυτό το άθροισμα σε μία άλλη μεταβλητή:
v = a[ 0 ] + a[ 1 ]
Εδώ έχουμε ένα σταθερό πλήθος εντολών, οπότε προκύπτει f( n ) = 1.
Το ακόλουθο πρόγραμμα σε C++ ελέγχει αν ένα vector (ένας πίνακας με φρου-φρου) που ονομάζεται A μεγέθους n περιέχει δύο ίδιες τιμές οπουδήποτε μέσα του:
bool duplicate = false;
for ( int i = 0; i < n; ++i ) {
for ( int j = 0; j < n; ++j ) {
if ( i != j && A[ i ] == A[ j ] ) {
duplicate = true;
break;
}
}
if ( duplicate ) {
break;
}
}
Καθώς εδώ έχουμε δύο φωλιασμένους βρόγχους τον ένα μέσα στον άλλο, θα έχουμε ασυμπτωτική συμπεριφορά που περιγράφεται από την f( n ) = n2.
Κανόνας της πιάτσας: Τα απλά προγράμματα μπορούν να αναλυθούν μετρώντας τους φωλιασμένους βρόγχους που υπάρχουν στο πρόγραμμα. Ένας απλός βρόγχος που διασχίζει n στοιχεία δίνει f( n ) = n. Ένας βρόγχος μέσα σ᾽ ένα βρόγχο δίνει f( n ) = n2. Ένας βρόγχος μέσα σ᾽ ένα βρόγχο μέσα σ᾽ ένα βρόγχο δίνει f( n ) = n3.
Αν έχουμε ένα πρόγραμμα που καλεί μια συνάρτηση μέσα σ᾽ ένα βρόγχο και ξέρουμε τον αριθμό των εντολών που χρειάζεται η συνάρτηση που καλείται, είναι εύκολο να αποφανθούμε για τον αριθμό των εντολών ολόκληρου του προγράμματος. Πράγματι, ας δούμε αυτό το παράδειγμα σε C:
int i;
for ( i = 0; i < n; ++i ) {
f( n );
}
Αν ξέρουμε ότι η f( n ) είναι μία συνάρτηση που πραγματοποιεί ακριβώς n εντολές, μπορούμε να ξέρουμε ότι ο αριθμός των εντολών όλου του προγράμματος θα είναι ασυμπτωτικά n2, καθώς η συνάρτηση καλείται ακριβώς n φορές.
Κανόνας της πιάτσας: Αν έχουμε μία σειρά από βρόγχους τον ένα μετά τον άλλο, ο πιο αργός από αυτούς καθορίζει την ασυμπτωτική συμπεριφορά του προγράμματος. Δύο φωλιασμένοι βρόγχοι ακολουθούμενοι από έναν απλό βρόγχο είναι ασυμπτωτικά το ίδιο σαν να είχαμε μόνο τους φωλιασμένους βρόγχους, επειδή οι φωλιασμένοι βρόγχοι υπερισχύουν έναντι του απλού.
Τώρα ας αρχίσουμε να χρησιμοποιούμε την κάπως ιδιότροπη γλώσσα που χρησιμοποιούν οι επιστήμονες των υπολογιστών. Όταν έχουμε βρει την ακριβή f ασυμπτωτικά, θα λέμε ότι το πρόγραμμά μας είναι Θ( f( n ) ). Για παράδειγμα, τα παραπάνω προγράμματα είναι Θ( 1 ), Θ( n2 ) και Θ( n2 ) αντίστοιχα. Το Θ( n ) διαβάζεται "θήτα του εν". Μερικές φορές λέμε ότι η f( n ), η αρχική συνάρτηση που μετρούσε τις εντολές μας συμπεριλαμβανομένων και των σταθερών όρων, είναι Θ( κάτι ). Για παράδειγμα, μπορούμε να πούμε ότι η f( n ) = 2n είναι μία συνάρτηση που είναι Θ( n ) — τίποτα καινούργιο προς το παρόν. Μπορούμε επίσης να γράφουμε 2n ∈ Θ( n ) το οποίο διαβάζεται "το δύο εν είναι θήτα του εν". Μην μπερδεύεστε με αυτά τα τα σύμβολα: Το μόνο που λένε είναι ότι αν μετρήσαμε τον αριθμό εντολών ενός προγράμματος και αυτές είναι 2n, τότε η ασυμπτωτική συμπεριφορά του αλγορίθμου μας περιγράφεται από το n, το οποίο βρίσκουμε πετώντας τις σταθερές. Δεδομένου αυτού του τρόπου γραφής, τα παρακάτω είναι μερικές αληθείς μαθηματικές προτάσεις:
- n6 + 3n ∈ Θ( n6 )
- 2n + 12 ∈ Θ( 2n )
- 3n + 2n ∈ Θ( 3n )
- nn + n ∈ Θ( nn )
Παρεμπιπτόντως, αν λύσατε την Άσκηση 1 παραπάνω, αυτές είναι ακριβώς οι απαντήσεις που θα πρέπει να βρήκατε.
Καλούμε αυτή τη συνάρτηση, δηλαδή αυτό που βάζουμε Θ( εδώ ), χρονική πολυπλοκότητα ή απλώς πολυπλοκότητα του αλγορίθμου μας. Οπότε ένας αλγόριθμος με Θ( n ) έχει πολυπλοκότητα n. Έχουμε επίσης ειδικά ονόματα για τα Θ( 1 ), Θ( n ), Θ( n2 ) και Θ( log( n ) ) επειδή εμφανίζονται ιδιαίτερα συχνά. Λέμε ότι ένας Θ( 1 ) αλγόριθμος είναι ένας αλγόριθμος σταθερού χρόνου, ένας Θ( n ) είναι γραμμικός, ένας Θ( n2 ) είναι τετραγωνικός και ένας Θ( log( n ) ) είναι λογαριθμικός (μην ανησυχείτε αν δεν ξέρετε ακόμα τι είναι οι λογάριθμοι – θα επιστρέψουμε σ᾽ αυτό σε ένα λεπτό).
Κανόνας της πιάτσας: Προγράμματα με μεγαλύτερο Θ τρέχουν πιο αργά από προγράμματα με μικρότερο Θ.

Συμβολισμός Big-O
Τώρα, είναι μερικές φορές δύσκολο να βρούμε την ακριβή συμπεριφορά ενός αλγορίθμου με τον τρόπο που κάναμε παραπάνω, ειδικά για πιο περίπλοκα παραδείγματα. Όμως θα μπορούμε να πούμε ότι η συμπεριφορά του αλγορίθμου μας δεν θα ξεπεράσει ποτέ ένα συγκεκριμένο φραγμα. Αυτό θα κάνει τη ζωή μας ευκολότερη, καθώς δεν θα χρειάζεται να πούμε επακριβώς πόσο γρήγορος είναι ο αλγόριθμός μας, ακόμη κι αν αγνοήσουμε τις σταθερές όπως κάναμε προηγουμένως. Το μόνο που θα χρειαστεί να κάνουμε είναι να βρούμε ένα ορισμένο φράγμα. Αυτό εξηγείται καλύτερα μ᾽ ένα παράδειγμα.
Ένα διάσημο πρόβλημα που οι επιστήμονες των υπολογιστών χρησιμοποιούν για να διδάξουν αλγορίθμους είναι το πρόβλημα ταξινόμησης. Στο πρόβλημα ταξινόμησης, μάς δίνεται ένας πίνακας A μεγέθους n (ακούγεται οικείο;) και μας ζητούν να γράψουμε ένα πρόγραμμα που ταξινομεί αυτό τον πίνακα. Το πρόβλημα αυτό είναι ενδιαφέρον διότι είναι ένα ρεαλιστικό πρόβλημα σε πραγματικά συστήματα. Για παράδειγμα, ένας περιηγητής αρχείων χρειάζεται να ταξινομήσει τα αρχεία που εμφανίζει με βάση το όνομα έτσι ώστε ο χρήστης να μπορεί να πλοηγηθεί με ευκολία. Ή, ως ένα ακόμη παράδειγμα, ένα βιντεοπαιχνίδι χρειάζεται να ταξινομήσει τα 3D αντικείμενα που εμφανίζει στον κόσμο με βάση τις αποστάσεις τους από το μάτι του παίκτη μέσα στον εικονικό κόσμο έτσι ώστε να αποφανθεί τι είναι ορατό και τι δεν είναι, κάτι που ονομάζεται Πρόβλημα Ορατότητας (βλ. Εικόνα 3). Τα αντικείμενα που βρίσκουμε ότι είναι κοντύτερα στον παίκτη είναι εκείνα που εμφανίζονται, ενώ εκείνα που είναι πιο απομακρυσμένα ενδέχεται να αποκρύπτονται από τα αντικείμενα που βρίσκονται μπροστά τους. Η ταξινόμηση είναι επίσης ενδιαφέρουσα επειδή υπάρχουν πολλοί αλγόριθμοι για να επιτευχθεί κάποιοι από τους οποίους είναι χειρότεροι από άλλους. Είναι επιπλέον ένα πρόβλημα με εύκολο ορισμό και εύκολη εξήγηση. Οπότε ας γράψουμε ένα τμήμα κώδικα που ταξινομεί ένα πίνακα.
Εδώ είναι ένας μη αποδοτικός τρόπος να υλοποιήσει κανείς την ταξινόμηση ενός πίνακα σε Ruby. (Φυσικά, η Ruby υποστηρίζει ενσωματωμένες μεθόδους για την ταξινόμηση πινάκων τις οποίες θα πρέπει να χρησιμοποιείτε αντ᾽ αυτής, και οι οποίες είναι σίγουρα γρηγορότερες από αυτά που θα δούμε εδώ. Αλλά αυτό υπάρχει εδώ για επεξηγηματικούς λόγους.)
b = []
n.times do
m = a[ 0 ]
mi = 0
a.each_with_index do |element, i|
if element < m
m = element
mi = i
end
end
a.delete_at( mi )
b << m
end
Αυτή είναι μία μέθοδος που ονομάζεται ταξινόμηση επιλογής. Βρίσκει το ελάχιστο στοιχείο του πίνακά μας (ο πίνακας παραπάνω σημειώνεται ως a, η ελάχιστη τιμή ως m και ο δείκτης της ως mi), το τοποθετεί στο τέλος ενός νέου πίνακα (στην περίπτωσή μας του b), και το διαγράφει από τον αρχικό πίνακα. Στη συνέχεια βρίσκει το ελάχιστο ανάμεσα στις τιμές που απομένουν στον αρχικό μας πίνακα, προσθέτει αυτή την τιμή στο νέο μας πίνακα έτσι ώστε τώρα να περιέχει δύο στοιχεία, και το αφαιρεί από τον αρχικό πίνακα. Συνεχίζει αυτή τη δουλειά έως ότου όλα τα στοιχεία να έχουν αφαιρεθεί από τον αρχικό πίνακα και έχουν προστεθεί στο νέο πίνακα, που σημαίνει ότι ο πίνακας έχει ταξινομηθεί. Σε αυτό το παράδειγμα, βλέπουμε ότι έχουμε δύο φωλιασμένους βρόγχους. Ο εξωτερικός βρόγχος τρέχει n φορές και ο εσωτερικός βρόγχος τρέχει μία φορά για κάθε στοιχείο του πίνακα a. Παρ᾽ όλο που ο πίνακας a έχει αρχικά n στοιχεία, αφαιρούμε ένα στοιχείο από τον πίνακα σε κάθε επανάληψη. Οπότε ο εσωτερικός βρόγχος επαναλαμβάνεται n κατά την πρώτη επανάληψη του εξωτερικού βρόγχου, στη συνέχεια n - 1 φορές, μετά n - 2 φορές και ούτω καθ᾽ εξής, έως την τελευταία επανάληψη του εξωτερικού βρόγχου κατά την οποία τρέχει μόνο μία φορά.
Είναι ελαφρώς δυσκολότερο να υπολογίσουμε την πολυπλοκότητα αυτού του προγράμματος, καθώς θα χρειαζόταν να βρούμε το άθροισμα 1 + 2 + ... + (n - 1) + n. Αλλά μπορούμε σίγουρα να βρούμε ένα "άνω φράγμα" της. Δηλαδή μπορούμε να αλλάξουμε το πρόγραμμά μας (αυτό μπορείτε να το κάνετε στο μυαλό σας, όχι στον καθεαυτό κώδικα) κάνοντάς το χειρότερο απ᾽ ό,τι είναι και στη συνέχεια βρίσκοντας την πολυπλοκότητα αυτού του νέου προγράμματος το οποίο παράξαμε. Αν μπορούμε να βρούμε την πολυπλοκότητα του χειρότερου προγράμματος που φτιάξαμε, τότε γνωρίζουμε ότι το αρχικό μας πρόγραμμα είναι το πολύ τόσο κακό, ή ίσως και καλύτερο. Μ᾽ αυτό τον τρόπο, αν βρούμε μία καλούτσικη πολυπλοκότητα για το αλλαγμένο μας πρόγραμμα, το οποίο είναι χειρότερο από το αρχικό μας, μπορούμε να ξέρουμε ότι το αρχικό μας θα έχει επίσης καλούτσικη πολυπλοκότητα – είτε όσο καλή όσο το αλλαγμένο μας πρόγραμμα ή και ακόμα καλύτερη.
Ας σκεφτούμε τώρα τον τρόπο να επεξεργαστούμε το πρόγραμμα στο παράδειγμα ώστε να διευκολύνουμε την εύρεση της πολυπλοκότητάς του. Αλλά ας κρατήσουμε κατά νου ότι επιτρέπεται μόνο να το χειροτερέψουμε, δηλαδή να το κάνουμε να τρέχει περισσότερες εντολές, έτσι ώστε η εκτίμησή μας να έχει νόημα για το αρχικό μας πρόγραμμα. Είναι προφανές ότι μπορούμε να αλλάξουμε τον εσωτερικό βρόγχο του προγράμματος έτσι ώστε να κάνει ακριβώς n επαναλήψεις κάθε φορά αντί για μεταβλητό πλήθος επαναλήψεων. Κάποιες από δαύτες θα είναι άχρηστες, αλλά θα μας βοηθήσουν να αναλύσουμε την πολυπλοκότητα του αλγορίθμου που θα προκύψει. Αν κάνουμε τούτη την απλή αλλαγή, τότε ο νέος αλγόριθμος που κατασκευάσαμε είναι εμφανώς Θ( n2 ), διότι έχουμε δύο φωλιασμένους βρόγχους εκ των οποίων ο καθένας επαναλαμβάνεται ακριβώς n φορές. Αν τα πράγματα είναι έτσι, θα λέμε ότι ο αρχικός μας αλγόριθμος είναι O( n2 ). Το O( n2 ) διαβάζεται "big oh του εν τετράγωνο" ή απλώς "ο του εν τετράγωνο". Αυτό που μας λέει αυτή η έκφραση είναι ότι το πρόγραμμά μας, ασυμπτωτικά, δεν θα είναι χειρότερο από n2. Μπορεί να είναι και καλύτερο απ᾽ αυτό, ή μπορεί να είναι το ίδιο. Παρεμπιπτόντως, αν το πρόγραμμά μας είναι πράγματι Θ( n2 ), μπορούμε ακόμη να λέμε ότι είναι O( n2 ). Για να το καταλάβετε αυτό, φανταστείτε να αλλάζατε το αρχικό σας πρόγραμμα όχι και πολύ, αλλά να το κάνατε ελαφρώς χειρότερο, προσθέτοντας ας πούμε μία επουσιώδη εντολή στην αρχή του προγράμματος. Κάνοντας κάτι τέτοιο μεταβάλλουμε τη συνάρτηση μέτρησης εντολών κατά μία απλή σταθερά, η οποία αγνοείται όταν μιλάμε για ασυμπτωτική συμπεριφορά. Οπότε ένα πρόγραμμα που είναι Θ( n2 ) είναι επίσης O( n2 ).
Όμως ένα πρόγραμμα που είναι O( n2 ) μπορεί να μην είναι Θ( n2 ). Για παράδειγμα, οποιοδήποτε πρόγραμμα είναι Θ( n ) είναι επίσης και O( n2 ) εκτός από το ότι είναι και O( n ). Αν φανταστούμε ότι ένα Θ( n ) πρόγραμμα αποτελείται από ένα απλό βρόγχο for που επαναλαμβάνεται n φορές, μπορούμε να το χειροτερέψουμε τοποθετώντας το μέσα σε ένα άλλο for που κι αυτό επαναλαμβάνεται n φορές, παράγοντας έτσι ένα πρόγραμμα με f( n ) = n2. Γενικεύοντας, οποιοδήποτε πρόγραμμα είναι Θ( a ) είναι O( b ) όταν το b είναι πιο κακό από το a. Σημειωτέον ότι οι αλλαγές που κάνουμε στο πρόγραμμα δεν είναι απαραίτητο να έχουν πραγματικά νόημα ή να δίνουν ένα ισοδύναμο πρόγραμμα με το αρχικό. Το μόνο που χρειάζεται είναι το νέο πρόγραμμα να τρέχει περισσότερες εντολές από το αρχικό για ένα δεδομένο n. Άλλωστε ο μόνος λόγος που το χρησιμοποιούμε είναι για να μετρήσουμε εντολές, όχι για να λύσουμε το πρόβλημα.
Οπότε, λέγοντας ότι το πρόγραμμά μας είναι O( n2 ) μιλάμε εκ του ασφαλούς: Αναλύσαμε τον αλγόριθμό μας και βρήκαμε ότι δεν είναι ποτέ χειρότερος από n2. Αλλά δεν αποκλείεται να είναι στην πραγματικότητα και n2. Αυτό μας δίνει μία καλή εκτίμηση για το πόσο γρήγορα τρέχει το πρόγραμμά μας. Οπότε ας εργαστούμε πάνω σε μερικά παραδείγματα για να βοηθήσουμε στην εξοικίωση με αυτό το νέο συμβολισμό.
Άσκηση 3
Βρείτε ποια από τα ακόλουθα είναι αλήθεια:
- Ένας Θ( n ) αλγόριθμος είναι O( n )
- Ένας Θ( n ) αλγόριθμος είναι O( n2 )
- Ένας Θ( n2 ) αλγόριθμος είναι O( n3 )
- Ένας Θ( n ) αλγόριθμος είναι O( 1 )
- Ένας O( 1 ) αλγόριθμος είναι Θ( 1 )
- Ένας O( n ) αλγόριθμος είναι Θ( 1 )
Λύση
- Αυτό ξέρουμε ότι ισχύει αφού το αρχικό μας πρόγραμμα ήταν Θ( n ). Μπορούμε να πετύχουμε O( n ) χωρίς καμία αλλαγή στο πρόγραμμά μας.
- Καθώς το n2 είναι χειρότερο από το n, τούτο είναι αλήθεια.
- Καθώς το n3 είναι χειρότερο από το n2, τούτο είναι αλήθεια.
- Καθώς το 1 δεν είναι χειρότερο από το n, τούτο είναι ψέματα. Αν ένα πρόγραμμα τρέχει ασυμπτωτικά n εντολές (ένα γραμμικό πλήθος εντολών), δεν μπορούμε να το κάνουμε χειρότερο και μετά να τρέχει ασυμπτωτικά μόνο 1 εντολή (ένα σταθερό πλήθος από εντολές).
- Τούτο είναι αλήθεια καθώς οι δύο πολυπλοκότητες είναι οι ίδιες.
- Τούτο μπορεί να είναι αλήθεια ή μπορεί και να μην είναι ανάλογα με τον αλγόριθμο. Στη γενική περίπτωση είναι ψέματα. Αν ένας αλγόριθμος είναι Θ( 1 ), τότε είναι σίγουρα O( n ). Όμως αν είναι O( n ) τότε μπορεί να μην είναι Θ( 1 ). Για παράδειγμα, ένας Θ( n ) αλγόριθμος είναι O( n ) αλλά όχι Θ( 1 ).
Άσκηση 4
Χρησιμοποιήστε το άθροισμα αριθμητικής προόδου για να αποδείξετε ότι το παραπάνω πρόγραμμα δεν είναι μόνο O( n2 ) αλλά και Θ( n2 ). Αν δεν ξέρετε τι είναι μια αριθμητική πρόοδος, βρείτε το στη Wikipedia – εύκολο είναι.
Επειδή η O-πολυπλοκότητα ενός αλγορίθμου δίνει ένα άνω φράγμα για την πραγματική πολυπλοκότητα του αλγορίθμου, ενώ το Θ δίνει την πραγματική πολυπλοκότητα του αλγορίθμου, λέμε μερικές φορές ότι το Θ μας δίνει ένα ακριβές φράγμα. Αν ξέρουμε ότι έχουμε βρει ένα φράγμα πολυπλοκότητας που δεν είναι ακριβές, μπορούμε επίσης να χρησιμοποιήσουμε το πεζό γράμμα o για να το δηλώσουμε. Για παράδειγμα, αν ένας αλγόριθμος είναι Θ( n ), τότε η ακριβής του πολυπλοκότητα είναι n. Έτσι, αυτός ο αλγόριθμος είναι τόσο O( n ) όσο και O( n2 ). Επειδή ο αλγόριθμος είναι Θ( n ), το φράγμα O( n ) ένα ένα ακριβές φράγμα. Όμως το φράγμα O( n2 ) δεν είναι ακριβές, κι έτσι μπορούμε να γράφουμε ότι ο αλγόριθμος είναι o( n2 ), το οποίο διαβάζεται "small oh του εν τετράγωνο" για να δείξουμε πως ξέρουμε ότι το φράγμα δεν είναι ακριβές. Είναι καλύτερα όταν μπορούμε να βρούμε ακριβή φράγματα για τους αλγορίθμους μας, αφού αυτά μας δίνουν περισσότερες πληροφορίες για τη συμπεριφορά του αλγορίθμου, όμως κάτι τέτοιο δεν είναι πάντα εύκολο.
Άσκηση 5
Βρείτε ποια από τα παρακάτω φράγματα είναι ακριβή και ποια δεν είναι. Ελέγξτε αν κάποιο φράγμα είναι λάθος. Χρησιμοποιήστε o( συμβολισμό ) για να δείξετε τα φράγματα που δεν είναι ακριβή.
- Ένας Θ( n ) αλγόριθμος για τον οποίο βρήκαμε ένα άνω φράγμα O( n ).
- Ένας Θ( n2 ) αλγόριθμος για τον οποίο βρήκαμε ένα άνω φράγμα O( n3 ).
- Ένας Θ( 1 ) αλγόριθμος για τον οποίο βρήκαμε ένα άνω φράγμα O( n ).
- Ένας Θ( n ) αλγόριθμος για τον οποίο βρήκαμε ένα άνω φράγμα O( 1 ).
- Ένας Θ( n ) αλγόριθμος για τον οποίο βρήκαμε ένα άνω φράγμα O( 2n ).
Λύση
- Σε αυτή την περίπτωση, η Θ πολυπλοκότητα και η O πολυπλοκότητα είναι οι ίδιες, οπότε το φράγμα είναι ακριβές.
- Εδώ βλέπουμε ότι η O πολυπλοκότητα είναι μεγαλύτερης κλίμακας από τη Θ πολυπλοκότητα οπότε αυτό το φράγμα δεν είναι ακριβές. Πράγματι, ένα φράγμα O( n2 ) θα ήταν ακριβές. Οπότε μπορούμε να γράψουμε ότι ο αλγόριθμος είναι o( n3 ).
- Και πάλι βλέπουμε ότι η O πολυπλοκότητα είναι μεγαλύτερης κλίμακας από τη Θ πολυπλοκότητα οπότε έχουμε ένα μη ακριβές φράγμα. Το φράγμα O( 1 ) θα ήταν ακριβές. Οπότε μπορούμε να επισημάνουμε ότι το O( n ) φράγμα δεν είναι ακριβές γράφοντάς το ως o( n ).
- Εδώ θα πρέπει να κάναμε κάποιο σφάλμα στον υπολογισμό αυτού του φράγματος, αφού είναι λάθος. Είναι αδύνατο ένας Θ( n ) αλγόριθμος να έχει άνω φράγμα O( 1 ), αφού το n είναι μεγαλύτερη πολυπλοκότητα από το 1. Θυμηθείτε ότι το O δίνει άνω φράγμα.
- Αυτό ίσως φαίνεται για φράγμα που δεν είναι ακριβές, όμως αυτό θα ήταν λάθος. Αυτό το φράγμα είναι στην πραγματικότητα ακριβές. Θυμηθείτε ότι η ασυμπτωτική συμπεριφορά των 2n και n είναι η ίδια, και ότι τα O και Θ ενδιαφέρονται μόνο για την ασυμπτωτική συμπεριφορά. Οπότε έχουμε ότι O( 2n ) = O( n ) και συνεπώς αυτό το φράγμα είναι ακριβές αφού η πολυπλοκότητα είναι η ίδια με το Θ.
Κανόνας της πιάτσας: Είναι ευκολότερο να βρούμε την O-πολυπλοκότητα ενός αλγορίθμου από το να βρούμε τη Θ-πολυπλοκότητά του.
Ίσως να νιώθετε ότι όλα αυτά τα νέα σύμβολα σάς έχουν πέσει λιγάκι βαριά μέχρι τώρα, αλλά ας εισάγουμε μόνο δύο επιπλέον σύμβολα πριν προχωρήσουμε σε παραδείγματα. Αυτά είναι εύκολα τώρα που γνωρίζετε για τα Θ, O και o, και αργότερα δεν θα τα χρησιμοποιήσουμε ιδιαίτερα σ᾽ αυτό το άρθρο, αλλά είναι καλό να τα ξέρετε μιας και αρχίσαμε. Στο παραπάνω παράδειγμα, επεξεργαστήκαμε το πρόγραμμά μας κάνοντάς το χειρότερο (δηλαδή κάνοντάς το να τρέχει περισσότερες εντολές και έτσι να χρειάζεται περισσότερο χρόνο) και κατασκευάσαμε έτσι το σύμβολο O. Το O έχει νόημα επειδή μας λέει ότι το πρόγραμμά μας δεν θα είναι ποτέ πιο αργό από ένα συγκεκριμένο φράγμα, κι έτσι μας προμηθεύει με πολύτιμες πληροφορίες που μπορούμε να χρησιμοποιήσουμε για να επιχειρηματολογήσουμε ότι το πρόγραμμά μας είναι αρκετά καλό. Αν κάνουμε το αντίθετο και αλλάξουμε το πρόγραμμά μας καλυτερεύοντάς το και υπολογίσουμε την πολυπλοκότητα του νέου προγράμματος, τότε χρησιμοποιούμε το συμβολισμό Ω. Το Ω συνεπώς μας δίνει μία πολυπλοκότητα που ξέρουμε ότι το πρόγραμμά μας δεν μπορεί να κερδίσει. Αυτό είναι χρήσιμο αν θέλουμε να αποδείξουμε ότι ένα πρόγραμμα είναι αργό ή ότι ένας αλγόριθμος είναι κακός. Χρησιμεύει για να επιχειρηματολογήσουμε υποστηρίζοντας ότι ένας αλγόριθμος είναι πολύ αργός για να χρησιμοποιηθεί σε κάποια συγκεκριμένη περίπτωση. Για παράδειγμα, λέγοντας ότι ένας αλγόριθμος είναι Ω( n3 ) σημαίνει ότι ο αλγόριθμός μας δεν είναι καλύτερος από n3. Μπορεί να είναι Θ( n3 ), ή ακόμη και Θ( n4 ) ή και ακόμα χειρότερος, αλλά ξέρουμε ότι είναι τουλάχιστον ένας κάπως κακός αλγόριθμος. Οπότε το Ω μας δίνει ένα κάτω φράγμα για την πολυπλοκότητα του αλγορίθμου μας. Όπως πριν είχαμε ο, τώρα μπορούμε να γράφουμε ω αν ξέρουμε ότι το φράγμα μας δεν είναι ακριβές. Για παράδειγμα, ένας Θ( n3 ) αλγόριθμος είναι ο( n4 ) και ω( n2 ). Το Ω( n ) διαβάζεται "big omega του εν", ενώ το ω( n ) διαβάζεται "small omega του εν". Είναι ενδιαφέρον εδώ να σημειώσουμε ότι παρ᾽ όλο που τα Ο και Ω είναι Ελληνικά γράμματα, είναι σοφότερο να χρησιμοποιούμε τις Αγγλικές εκφράσεις "big oh", "big omega", "small oh" και "small omega" διότι το μπέρδεμα είναι μεγάλο αν χρησιμοποιούμε Ελληνικές εκφράσεις όπως "μεγάλο ο μικρόν" και "μικρό ω μέγα".
Άσκηση 6
Για τις ακόλουθες Θ πολυπλοκότητες γράψτε ένα ακριβές και ένα μη ακριβές φϱαγμα O καθώς και ένα ακριβές και μη ακριβές φράγμα Ω της επιλογής σας, υπό την προϋπόθεση ότι υπάρχουν.
- Θ( 1 )
- Θ(
 )
) - Θ( n )
- Θ( n2 )
- Θ( n3 )
Λύση
Αυτό δεν είναι παρά μία άμεση εφαρμογή των παραπάνω ορισμών.
- Τα ακριβή φράγματα θα είναι O( 1 ) και Ω( 1 ). Ένα μη ακριβές O-φράγμα θα ήταν το O( n ). Θυμηθείτε ότι το O μας δίνει ένα άνω φράγμα. Καθώς το n είναι μεγαλύτερης κλίμακας από το 1 αυτό είναι ένα μη-ακριβές φράγμα και μπορούμε να το γράψουμε και ως o( n ). Όμως εδώ δεν μπορούμε να βρούμε ένα μη-ακριβές φράγμα για το Ω, καθώς δεν μπορούμε να πέσουμε κάτω από το 1 γι᾽ αυτές τις συναρτήσεις. Οπότε θα πρέπει να αρκεστούμε στο ακριβές φράγμα.
- Τα ακριβή φράγματα θα είναι τα ίδια με την Θ πολυπλοκότητα, οπότε είναι O(
 ) και Ω(
) και Ω(  ) αντιστοίχως. Για τα μη-ακριβή φράγματα μπορούμε να πάρουμε το O( n ), καθώς το n είναι μεγαλύτερο από το
) αντιστοίχως. Για τα μη-ακριβή φράγματα μπορούμε να πάρουμε το O( n ), καθώς το n είναι μεγαλύτερο από το  και έτσι είναι ένα άνω φράγμα για το
και έτσι είναι ένα άνω φράγμα για το  . Καθώς ξέρουμε ότι αυτό είναι ένα μη ακριβές άνω φράγμα, μπορούμε να το γράψουμε και o( n ). Για μη ακριβές κάτω φράγμα μπορούμε απλώς να χρησιμοποιήσουμε το Ω( 1 ). Καθώς ξέρουμε ότι αυτό το φράγμα δεν είναι ακριβές, μπορούμε να το γράψουμε και ως ω( 1 ).
. Καθώς ξέρουμε ότι αυτό είναι ένα μη ακριβές άνω φράγμα, μπορούμε να το γράψουμε και o( n ). Για μη ακριβές κάτω φράγμα μπορούμε απλώς να χρησιμοποιήσουμε το Ω( 1 ). Καθώς ξέρουμε ότι αυτό το φράγμα δεν είναι ακριβές, μπορούμε να το γράψουμε και ως ω( 1 ). - Τα ακριβή φράγματα είναι O( n ) και Ω( n ). Δύο μη ακριβή φράγματα θα μπορούσε να είναι τα ω( 1 ) και o( n3 ). Αυτά είναι στην πραγματικότητα αρκετά άσχημα φράγματα, καθώς είναι μακριά από της αρχικές μας πολυπλοκότητες, αλλά παραμένουν έγκυρα με βάση τους ορισμούς μας.
- Τα ακριβή φράγματα είναι O( n2 ) και Ω( n2 ). Για τα μη ακριβή φράγματα θα μπορούσαμε και πάλι να χρησιμοποιήσουμε τα ω( 1 ) και o( n3 ) όπως στο προηγούμενο παράδειγμα.
- Τα ακριβή φράγματα είναι O( n3 ) και Ω( n3 ) αντίστοιχα. Δύο μη ακριβή φράγματα θα μπορούσαν να είναι τα ω(
 n2 ) και o(
n2 ) και o(  n3 ). Παρ᾽ όλο που αυτά τα φράγματα δεν είναι ακριβή, είναι καλύτερα από αυτά που δώσαμε παραπάνω.
n3 ). Παρ᾽ όλο που αυτά τα φράγματα δεν είναι ακριβή, είναι καλύτερα από αυτά που δώσαμε παραπάνω.
Ο λόγος που χρησιμοποιούμε τα O και Ω αντί του Θ παρ᾽ όλο που τα O και Ω μπορούν να δώσουν κι αυτά ακριβή φράγματα είναι ότι μπορεί να μην μπορούμε να ξέρουμε αν ένα φράγμα που βρήκαμε είναι ακριβές, ή μπορεί απλώς να μη θέλουμε να μπούμε στη διαδικασία να το ψειρίσουμε τόσο πολύ.
Αν δε θυμάστε όλα τα διαφορετικά σύμβολα και τις χρήσεις τους, μη σας νοιάζει και τόσο αυτή τη στιγμή. Μπορείτε πάντα να επιστρέψετε σε αυτή την ενότητα για να τα βρείτε. Τα σημαντικότερα σύμβολα είναι το O και το Θ.
Ας σημειώσουμε εδώ ότι παρ᾽ όλο που το Ω μας δίνει ένα κάτω φράγμα για τη συνάρτησή μας (δηλαδή έχουμε βελτιώσει το πρόγραμμά μας και το έχουμε κάνει να τρέχει λιγότερες εντολές) συνεχίζουμε να αναφερόμαστε σε ανάλυση "χειρότερης περίπτωσης". Τούτο διότι ταΐζουμε το πρόγραμμά μας τη χειρότερη δυνατή είσοδο για το n που μας ενδιαφέρει και αναλύουμε τη συμπεριφορά του κάτω από αυτή την υπόθεση.
Ο παρακάτω πίνακας συνοψίζει τα σύμβολα που μόλις εισάγαμε και τις αντιστοιχίες τους με τα συνήθη μαθηματικά σύμβολα που χρησιμοποιούμε για τους αριθμούς. Ο λόγος που δεν χρησιμοποιούμε τα συνήθη σύμβολα εδώ αλλά Ελληνικά γράμματα είναι για να δείξουμε ότι κάνουμε μία σύγκριση σε ασυμπτωτικό επίπεδο, και όχι μία απλή σύγκριση.
| Τελεστής ασυμπτωτικής σύγκρισης | Τελεστής αριθμητικής σύγκρισης |
|---|---|
| Ο αλγόριθμός μας είναι o( κάτι ) | Ένας αριθμός είναι < κάτι |
| Ο αλγόριθμός μας είναι O( κάτι ) | Ένας αριθμός είναι ≤ κάτι |
| Ο αλγόριθμός μας είναι Θ( κάτι ) | Ένας αριθμός είναι = κάτι |
| Ο αλγόριθμός μας είναι Ω( κάτι ) | Ένας αριθμός είναι ≥ κάτι |
| Ο αλγόριθμός μας είναι ω( κάτι ) | Ένας αριθμός είναι > κάτι |
Κανόνας της πιάτσας: Παρ᾽ όλο που όλα τα σύμβολα O, o, Ω, ω και Θ είναι χρήσιμα πού και πού, το O είναι εκείνο που χρησιμοποιείται περισσότερο, αφού είναι ευκολότερο να βρεθεί από το Θ και πιο πρακτικό από το Ω.
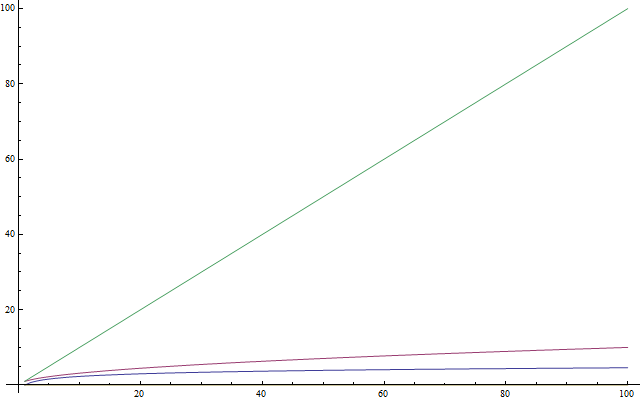
Λογάριθμοι
Αν ξέρετε τι είναι οι λογάριθμοι, μπορείτε να προσπεράσετε αυτή την ενότητα. Καθώς πολλοί άνθρωποι δεν είναι εξοικειωμένοι με τους λογαρίθμους, ή απλώς δεν τους έχουν χρησιμοποιήσει και πολύ τώρα τελευταία και δεν τους θυμούνται, αυτή η ενότητα είναι εδώ ως μία εισαγωγή γι᾽ αυτούς. Αυτό το κείμενο είναι επίσης για τους μικρότερους μαθητές που δεν έχουν συναντήσει τους λογαρίθμους στο σχολείο ακόμα. Οι λογάριθμοι είναι σημαντικοί επειδή εμφανίζονται πολύ στην ανάλυση πολυπλοκότητας. Ένας λογάριθμος είναι μία πράξη που εφαρμόζεται σε έναν αριθμό που τον κάνει αρκετά μικρότερο – όπως η τετραγωνική ρίζα ενός αριθμού. Οπότε αν υπάρχει ένα πράγμα που θα διαλέξετε να θυμάστε για τους λογαρίθμους είναι ότι παίρνουν έναν αριθμό και τον κάνουν πολύ μικρότερο από τον αρχικό (βλ. Εικόνα 4). Τώρα, με τον ίδιο τρόπο που η τετραγωνική ρίζα είναι η αντίστροφη πράξη του τετραγωνισμού, έτσι οι λογάριθμοι είναι η αντίστροφη πράξη της ύψωσης σε εκθέτη. Δεν είναι όσο δύσκολο όσο ακούγεται. Ας το εξηγήσουμε καλύτερα με ένα παράδειγμα. Πάρτε την εξίσωση:
2x = 1024
Θέλουμε τώρα να λύσουμε αυτή την εξίσωση ως προς x. Οπότε ρωτάμε: Ποιος είναι ο αριθμός στον οποίο πρέπει να υψώσουμε τη βάση 2 ώστε να πάρουμε 1024; Αυτός ο αριθμός είναι το 10. Όντως, έχουμε 210 = 1024, το οποίο επιβεβαιώνεται εύκολα. Οι λογάριθμοι μας επιτρέπουν να μιλήσουμε γι᾽ αυτό το πρόβλημα χρησιμοποιώντας ένα νέο συμβολισμό. Στην περίπτωσή μας, το 10 είναι ο λογάριθμος του 1024 και το γράφουμε log( 1024 ) και το διαβάζουμε "ο λογάριθμος του 1024". Επειδή χρησιμοποιούμε ως βάση το 2, αυτοί οι λογάριθμοι λέγονται δυαδικοί. Υπάρχουν λογάριθμοι και σε άλλες βάσεις, αλλά εμείς θα χρησιμοποιήσουμε μόνο δυαδικούς σε αυτό το άρθρο. Αν είστε μαθητής που διαγωνίζεται σε διεθνής διαγωνισμούς και δεν ξέρετε λογαρίθμους, σας προτρέπω να εξασκηθείτε στους λογαρίθμους αφού τελειώστε με αυτό το άρθρο. Στην επιστήμη των υπολογιστών, οι λογάριθμοι με βάση το 2 είναι πολύ πιο συνηθισμένοι από οποιουσδήποτε άλλους. Αυτό συμβαίνει επειδή συχνά έχουμε να κάνουμε με μόνο δύο διαφορετικές οντότητες: 0 και 1. Επιπλέον τείνουμε να κόβουμε ένα μεγάλο πρόβλημα στη μέση, παίρνοντας έτσι δύο μισά. Οπότε χρειάζεται να ξέρετε μόνο για τους λογάριθμους με βάση το 2 για να συνεχίσετε με αυτό το άρθρο.
Άσκηση 7
Λύστε τις παρακάτω εξισώσεις. Δείξτε ποιον λογάριθμο υπολογίζετε σε κάθε περίπτωση. Χρησιμοποιήστε μόνο λογαρίθμους με βάση το 2.
- 2x = 64
- (22)x = 64
- 4x = 4
- 2x = 1
- 2x + 2x = 32
- (2x) * (2x) = 64
Λύση
Δεν έχουμε να κάνουμε τίποτα άλλο παρά να εφαρμόσουμε τις ιδέες που ορίσαμε.
- Δοκιμάζοντας βρίσκουμε ότι x = 6 και άρα log( 64 ) = 6.
- Εδώ παρατηρούμε ότι το (22)x, από τις ιδιότητες των δυνάμεων, γράφεται 22x. Οπότε έχουμε 2x = 6 επειδή log( 64 ) = 6 από το προηγούμενο αποτέλεσμα και άρα x = 3.
- Χρησιμοποιώντας τις γνώσεις μας από την προηγούμενη εξίσωση, μπορούμε να γράψουμε το 4 ως 22 κι έτσι η εξίσωσή μας γίνεται (22)x = 4 που είναι το ίδιο με το 22x = 4. Στη συνέχεια παρατηρούμε ότι log( 4 ) = 2 επειδή 22 = 4 και άρα έχουμε 2x = 2. Άρα x = 1. Αυτό φαίνεται και ξεκάθαρα στην αρχική εξίσωση, αφού χρησιμοποιώντας τον εκθέτη 1 μας δίνει τη βάση ως αποτέλεσμα.
- Θυμηθείτε ότι ο εκθέτης 0 δίνει αποτέλεσμα 1. Οπότε έχουμε ότι log( 1 ) = 0 αφού 20 = 1 και άρα x = 0.
- Εδώ έχουμε ένα άθροισμα και έτσι δεν μπορούμε να βρούμε το λογάριθμο άμεσα. Όμως παρατηρούμε ότι το 2x + 2x είναι το ίδιο με το 2 * (2x). Οπότε έχουμε πολλαπλασιάσει ένα επιπλέον δυάρι, και έτσι αυτό είναι το ίδιο με το 2x + 1 και τώρα το μόνο που απομένει να κάνουμε είναι να λύσουμε την εξίσωση 2x + 1 = 32. Βρίσκουμε ότι log( 32 ) = 5 και είναι x + 1 = 5 άρα x = 4.
- Πολλαπλασιάζουμε μεταξύ τους δύο δυνάμεις του 2 κι έτσι μπορούμε να τις ενώσουμε παρατηρώντας ότι το (2x) * (2x) είναι το ίδιο με το 22x. Στη συνέχεια το μόνο που μένει να κάνουμε είναι να λύσουμε την εξίσωση 22x = 64 που έχουμε ήδη λύσει πιο πάνω και άρα x = 3.
Κανόνας της πιάτσας: Για αλγορίθμους διαγωνισμών υλοποιημένους σε C++, μόλις αναλύσετε την πολυπλοκότητά σας, μπορείτε να βρείτε στο περίπου πόσο γρήγορα θα τρέξει το πρόγραμμά σας θεωρώντας ότι μπορεί να κάνει περίπου 1,000,000 πράξεις το δευτερόλεπτο, όπου οι πράξεις που μετράτε δίνονται από τη συνάρτηση που περιγράφει την ασυμπτωτική συμπεριφορά του αλγορίθμου σας. Για παράδειγμα, ένας αλγόριθμος Θ( n ) χρειάζεται περίπου ένα δευτερόλεπτο για να επεξεργαστεί είσοδο με n = 1,000,000.
Αναδρομική πολυπλοκότητα
Ας δούμε τώρα μία αναδρομική συνάρτηση. Μία αναδρομική συνάρτηση είναι κάποια συνάρτηση που καλεί τον εαυτό της. Μπορούμε να αναλύσουμε την πολυπλοκότητά της; Η ακόλουθη συνάρτηση, γραμμένη σε Python, υπολογίζει το παραγοντικό ενός αριθμού. Το παραγοντικό ενός φυσικού αριθμού το βρίσκουμε πολλαπλασιάζοντας όλους τους προηγούμενους φυσικούς αριθμούς μεταξύ τους. Για παράδειγμα, το παραγοντικό του 5 είναι 5 * 4 * 3 * 2 * 1. Το γράφουμε "5!" και το διαβάζουμε "πέντε παραγοντικό" (μερικοί άνθρωποι προτιμούν να το διαβάζουν φωνάζοντάς το δυνατά: "ΠΕΝΤΕ!!!")
def factorial( n ):
if n == 1:
return 1
return n * factorial( n - 1 )
Ας αναλύσουμε την πολυπλοκότητα αυτής της συνάρτησης. Αυτή η συνάρτηση δεν έχει καθόλου βρόγχους, αλλά η πολυπλοκότητά της δεν είναι σταθερή. Αυτό που πρέπει να κάνουμε για να υπολογίσουμε την πολυπλοκότητά της είναι ξανά να αρχίσουμε να μετράμε εντολές. Είναι εμφανές ότι, αν δώσουμε κάποιο n σε αυτή τη συνάρτηση, θα εκτελέσει τον εαυτό της n φορές. Αν δεν είστε πεπεισμένος γι᾽ αυτό, τρέξτε την τώρα "στο χέρι" για n = 5 για να επιβεβαιώσετε ότι πραγματικά λειτουργεί. Για παράδειγμα, για n = 5, θα τρέξει 5 φορές, καθώς θα μειώνει συνεχώς το n κατά 1 σε κάθε κλήση. Μπορούμε λοιπόν να δούμε ότι αυτή η συνάρτηση είναι Θ( n ).
Αν είστε αβέβαιος γι᾽ αυτό, θυμηθείτε ότι μπορείτε να βρείτε την ακριβή πολυπλοκότητα μετρώντας εντολές. Αν το επιθυμείτε, μπορείτε τώρα να μετρήσετε τις εντολές που πραγματικά εκτελεί αυτή η συνάρτηση και να βρείτε μία συνάρτηση f( n ) και να δείτε ότι είναι πραγματικά γραμμική (θυμηθείτε ότι γραμμική σημαίνει Θ( n )).
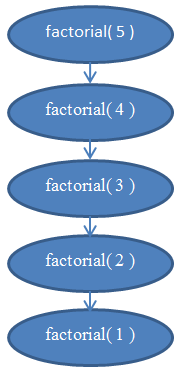
Δείτε την Εικόνα 5 για ένα διάγραμμα που θα σας κατατοπίσει σχετικά με τις αναδρομικές κλήσεις που εκτελεί η factorial( 5 ).
Αυτό θα πρέπει να ξεκαθαρίσει τα πράγματα σχετικά με το γιατί αυτή η συνάρτηση έχει γραμμική πολυπλοκότητα.
Λογαριθμική πολυπλοκότητα
Ένα διάσημο πρόβλημα στην επιστήμη των υπολογιστών είναι αυτό της αναζήτησης μίας τιμής μέσα σ᾽ ένα πίνακα. Λύσαμε το πρόβλημα στη γενική του μορφή νωρίτερα. Αυτό το πρόβλημα γίνεται ενδιαφέρον αν έχουμε ένα πίνακα που είναι ταξινομημένος και θέλουμε να βρούμε κάποια τιμή μέσα του. Μία μέθοδος που μπορούμε να χρησιμοποιήσουμε για να λύσουμε αυτό το πρόβλημα λέγεται δυαδική αναζήτηση. Κοιτάμε το μεσαίο στοιχείο του πίνακά μας: Αν βρούμε την τιμή εκεί, τελειώσαμε. Διαφορετικά, αν η τιμή που βρούμε εκεί είναι μεγαλύτερη από την τιμή που ψάχνουμε, τότε ξέρουμε ότι το στοιχείο μας θα είναι στο αριστερό μέρος του πίνακα. Σε διαφορετική περίπτωση, ξέρουμε ότι θα βρίσκεται στο δεξί μέρος του πίνακα. Μπορούμε να συνεχίσουμε να κόβουμε αυτούς τους μικρότερους πίνακες στη μέση μέχρι να έχουμε να κάνουμε με ένα μόνο στοιχείο. Εδώ είναι η μέθοδος σε ψευδοκώδικα:
def binarySearch( A, n, value ):
if n = 1:
if A[ 0 ] = value:
return true
else:
return false
if value < A[ n / 2 ]:
return binarySearch( A[ 0...( n / 2 - 1 ) ], n / 2 - 1, value )
else if value > A[ n / 2 ]:
return binarySearch( A[ ( n / 2 + 1 )...n ], n / 2 - 1, value )
else:
return true
Αυτός ο ψευδοκώδικας είναι μια απλοποίηση της πραγματικής υλοποίησης. Στην πράξη, αυτή η μέθοδος είναι πιο εύκολη στα λόγια απ᾽ ό,τι στην υλοποίηση, αφού ο προγραμματιστής πρέπει να χειριστεί μερικά ζητήματα υλοποίησης. Υπάρχουν σφάλματα off-by-one και η διαίρεση με το 2 μπορεί να μη δώσει πάντοτε ακέραιο αποτέλεσμα και άρα είναι απαραίτητο να χρησιμοποιήσουμε floor() ή ceil() στην τιμή. Αλλά μπορούμε για τους σκοπούς μας να υποθέσουμε ότι θα πετυχαίνει πάντα, και θα υποθέσουμε ότι η υλοποίηση στην πραγματικότητα φροντίζει για τα σφάλματα off-by-one, καθώς εμείς θέλουμε μόνο να αναλύσουμε την πολυπλοκότητα αυτής της μεθόδου. Αν δεν έχετε υλοποιήσει ποτέ τη δυαδική αναζήτηση, ίσως θα ήταν καλή ιδέα να το κάνετε αυτό τώρα στην αγαπημένη σας γλώσσα προγραμματισμού. Είναι μία πραγματικά διαφωτιστική περιπέτεια.
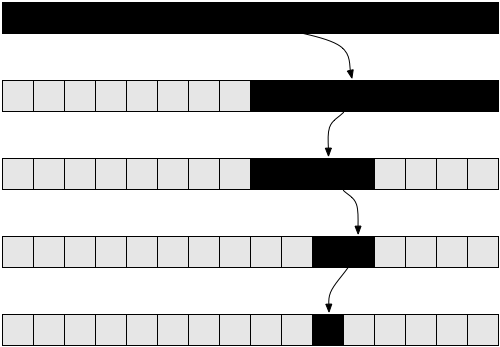
Δείτε την Εικόνα 6 για να σας βοηθήσει να καταλάβετε τον τρόπο που λειτουργεί η δυαδική αναζήτηση.
Αν είστε αβέβαιος για το ότι αυτή η μέθοδος πραγματικά δουλεύει, αφιερώστε τώρα ένα λεπτό για να την τρέξετε "στο χέρι" σε κάποιο απλό παράδειγμα για να πεισθείτε ότι πραγματικά δουλεύει.
Ας προσπαθήσουμε τώρα να αναλύσουμε αυτόν τον αλγόριθμο. Και πάλι έχουμε έναν αναδρομικό αλγόριθμο σ᾽ αυτή την περίπτωση. Ας υποθέσουμε, για απλούστευση, ότι ο πίνακας κόβεται ακριβώς στη μέση πάντα, αγνοώντας για τώρα τα + 1 και - 1 στην αναδρομική κλήση. Θα πρέπει να έχετε πεισθεί μέχρι στιγμής ότι μία μικρή αλλαγή όπως το να αγνοήσουμε τα + 1 και - 1 δεν θα επηρεάσει τα αποτελέσματα της πολυπλοκότητάς μας. Αυτό είναι κάτι που θα έπρεπε κανονικά να αποδείξουμε αν θέλουμε να είμαστε μαθηματικά φρόνιμοι, αλλά πρακτικά είναι προφανές από τη διαίσθησή μας. Ας υποθέσουμε ότι ο πίνακάς μας έχει μέγεθος που είναι τέλεια δύναμη του 2, για απλότητα. Και πάλι αυτό είναι μία υπόθεση που δεν θα αλλάξει τα τελικά μας αποτελέσματα πολυπλοκότητας στα οποία θα καταλήξουμε. Η χειρότερη περίπτωση γι᾽ αυτό το πρόβλημα συμβαίνει όταν η τιμή που ψάχνουμε δεν εμφανίζεται καν μέσα στον πίνακά μας. Σ᾽ αυτή την περίπτωση, θα ξεκινήσουμε με ένα πίνακα μεγέθους n στην πρώτη κλήση της αναδρομής και στη συνέχεια θα έχουμε ένα πίνακα μεγέθους n / 2 στην επόμενη κλήση. Στη συνέχεια θα έχουμε ένα πίνακα μεγέθους n / 4 στην επόμενη αναδρομική κλήση, ακολουθούμενο από έναν πίνακα μεγέθους n / 8 και ούτω καθεξής. Γενικά, ο πίνακάς μας σπάει στη μέση σε κάθε κλήση, έως ότου φτάσουμε στο 1 στοιχείο. Οπότε ας γράψουμε τον αριθμό των στοιχείων του πίνακα για κάθε κλήση:
Παρατηρήστε ότι στην i-οστή επανάληψη, ο πίνακάς μας έχει n / 2i στοιχεία. Αυτό συμβαίνει επειδή σε κάθε επανάληψη κόβουμε τον πίνακα στη μέση, που σημαίνει ότι διαιρούμε το πλήθος των στοιχείων του με το δύο. Αυτό μεταφράζεται σε έναν πολλαπλασιασμό του παρονομαστή με το 2. Αν αυτό το κάνουμε i φορές, παίρνουμε το n / 2i. Τώρα, αυτή η διαδικασία συνεχίζει και με κάθε μεγαλύτερο i παίρνουμε και ένα μικρότερο πλήθος στοιχείων έως ότου φτάσουμε στην τελευταία επανάληψη στην οποία έχουμε μείνει με μόνο 1 στοιχείο. Αν θέλουμε να βρούμε το i έτσι ώστε να δούμε σε ποια επανάληψη θα συμβεί αυτό, πρέπει να λύσουμε την ακόλουθη εξίσωση:
1 = n / 2i
Αυτό θα ισχύει μόνο όταν θα έχουμε φτάσει στην τελευταία κλήση της συνάρτησης binarySearch() και όχι στη γενική περίπτωση. Οπότε λύνοντας εδώ ως προς i μας βοηθά να βρούμε σε ποια επανάληψη η αναδρομή θα τελειώσει. Πολλαπλασιάζοντας και τα δύο μέλη με το 2i παίρνουμε:
2i = n
Τώρα, αυτή η εξίσωση θα πρέπει να σας φαίνεται γνωστή αν διαβάσατε την παραπάνω ενότητα περί λογαρίθμων. Λύνοντας ως προς i έχουμε:
i = log( n )
Αυτό μας λέει ότι ο αριθμός των επαναλήψεων που χρειάζεται για να κάνουμε δυαδική αναζήτηση είναι log( n ) όπου n είναι ο αριθμός των στοιχείων του αρχικού μας πίνακα.
Αν το σκεφτείτε, αυτό το πράγμα βγάζει νόημα. Για παράδειγμα, πάρτε το n = 32, έναν πίνακα δηλαδή με 32 στοιχεία. Πόσες φορές θα πρέπει να κόψουμε αυτό τον πίνακα στη μέση ώστε να μας μείνει μόνο 1 στοιχείο; Έχουμε: 32 → 16 → 8 → 4 → 2 → 1. Το κάναμε 5 φορές, που είναι και ο λογάριθμος του 32. Γι᾽ αυτό το λόγο η πολυπλοκότητα της δυαδικής αναζήτησης είναι Θ( log( n ) ).
Αυτό το τελευταίο αποτέλεσμα μας επιτρέπει να συγκρίνουμε τη δυαδική αναζήτηση με τη γραμμική αναζήτηση που ήταν η προηγούμενη μέθοδος που χρησιμοποιήσαμε. Είναι ξεκάθαρο ότι, αφού το log( n ) είναι πολύ μικρότερο του n, είναι λογικό να συμπεράνουμε ότι η δυαδική αναζήτηση είναι μία πολύ πιο γρήγορη μέθοδος αναζήτησης μέσα σε πίνακα από τη γραμμική αναζήτηση, οπότε ίσως είναι σοφό να κρατάμε τους πίνακές μας ταξινομημένους αν σκοπεύουμε να κάνουμε πολλές αναζητήσεις μέσα τους.
Κανόνας της πιάτσας: Η βελτίωση του ασυμπτωτικού χρόνου εκτέλεσης ενός αλγορίθμου συχνά βελτιώνει την επίδοσή του δραματικά, πολύ περισσότερο από μικρότερες "τεχνικές" βελτιστοποιήσεις όπως η χρήση μίας γρηγορότερης γλώσσας προγραμματισμού.
Βέλτιστη ταξινόμηση
Συγχαρητήρια. Μάθατε για την ανάλυση πολυπλοκότητας αλγορίθμων, την ασυμπτωτική συμπεριφορά συναρτήσεων και το συμβολισμό big-O. Ξέρετε επίσης πλέον να αποφασίζετε διαισθητικά ότι η πολυπλοκότητα ενός αλγορίθμου είναι O( 1 ), O( log( n ) ), O( n ), O( n2 ) και τα λοιπά. Ξέρετε τα σύμβολα o, O, ω, Ω και Θ και τι σημαίνει ανάλυση χειρότερης περίπτωσης. Αν φτάσατε μέχρι εδώ, αυτό το άρθρο πέτυχε ήδη το σκοπό του.
Αυτή η τελευταία ενότητα είναι προαιρετική. Είναι ελαφρώς πιο περίπλοκη, οπότε μπορείτε να την προσπεράσετε αν νιώθετε ότι είναι πολύ βαθιά νερά για εσάς. Απαιτεί τη συγκέντρωσή σας και θα χρειαστεί να αφιερώσετε μερικά λεπτά και να δουλέψετε πάνω στις ασκήσεις. Παρ᾽ όλα αυτά, θα σας προμηθεύσει με μία πολύ χρήσιμη μέθοδο στην ανάλυση πολυπλοκότητας αλγορίθμων που μπορεί να γίνει πολύ δυνατή, οπότε σίγουρα αξίζει τον κόπο να την καταλάβετε.
Παραπάνω είδαμε μία μέθοδο ταξινόμησης που λέγεται ταξινόμηση επιλογής. Αναφέραμε ότι η ταξινόμηση επιλογής δεν είναι βέλτιστη. Ένας βέλτιστος αλγόριθμος είναι ένας αλγόριθμος που λύνει ένα πρόβλημα με τον καλύτερο δυνατό τρόπο που σημαίνει ότι δεν υπάρχουν καλύτεροι αλγόριθμοι για το πρόβλημα αυτό. Αυτό σημαίνει ότι όλοι οι άλλοι αλγόριθμοι που λύνουν αυτό το πρόβλημα έχουν χειρότερη ή ίδια πολυπλοκότητα με τον βέλτιστο αυτό αλγόριθμο. Μπορεί να υπάρχουν πολλοί βέλτιστοι αλγόριθμοι για ένα πρόβλημα που όλοι μοιράζονται την ίδια πολυπλοκότητα. Το πρόβλημα ταξινόμησης μπορεί να λυθεί βέλτιστα με ποικίλους τρόπους. Μπορούμε να χρησιμοποιήσουμε την ίδια ιδέα με τη δυαδική αναζήτηση για να ταξινομήσουμε γρήγορα. Αυτή η μέθοδος ονομάζεται ταξινόμηση συγχώνευσης.
Για να κάνουμε ταξινόμηση με συγχώνευση, θα χρειαστεί αρχικά να κατασκευάσουμε μία βοηθητική συνάρτηση που θα χρησιμοποιήσουμε όταν θα έρθει η ώρα να κάνουμε την ταξινόμηση. Θα φτιάξουμε μία συνάρτηση merge που παίρνει δύο πίνακες που είναι και οι δύο ήδη ταξινομημένοι και τους συγχωνεύει σε ένα μεγάλο ταξινομημένο πίνακα. Αυτό γίνεται εύκολα:
def merge( A, B ):
if empty( A ):
return B
if empty( B ):
return A
if A[ 0 ] < B[ 0 ]:
return concat( A[ 0 ], merge( A[ 1...A_n ], B ) )
else:
return concat( B[ 0 ], merge( A, B[ 1...B_n ] ) )
Η συνάρτηση concat παίρνει ένα στοιχείο, την "κεφαλή", και ένα πίνακα, την "ουρά", και κατασκευάζει και επιστρέφει ένα νέο πίνακα που περιέχει το δεδομένο στοιχείο "κεφαλή" ως το πρώτο στοιχείο στο νέο πίνακα και τη δεδομένη "ουρά" ως τα υπόλοιπα στοιχεία του πίνακα. Για παράδειγμα, το concat( 3, [ 4, 5, 6 ] ) επιστρέφει [ 3, 4, 5, 6 ]. Γράφουμε A_n και B_n συμβολίζοντας τα μεγέθη των πινάκων Α και Β αντίστοιχα.
Άσκηση 8
Επιβεβαιώστε ότι η παραπάνω συνάρτηση πραγματικά πραγματοποιεί συγχώνευση. Ξαναγράψτε την στην αγαπημένη σας γλώσσα προγραμματισμού με επαναληπτικό τρόπο (χρησιμοποιώντας βρόγχους for) αντί για αναδρομικά.
Η ανάλυση αυτού του αλγορίθμου αποκαλύπτει ότι ο χρόνος εκτέλεσής του είναι Θ( n ), όπου n είναι το μέγεθος του πίνακα που προκύπτει (n = A_n + B_n).
Άσκηση 9
Επιβεβαιώστε ότι ο χρόνος εκτέλεσης της merge είναι Θ( n ).
Αξιοποιώντας αυτή τη συνάρτηση μπορούμε να κατασκευάσουμε έναν καλύτερο αλγόριθμο ταξινόμησης. Η ιδέα είναι η ακόλουθη: Χωρίζουμε τον πίνακά μας σε δύο μέρη. Ταξινομούμε καθένα από αυτά τα δύο μέρη αναδρομικά και στη συνέχεια συγχωνεύουμε τα δύο ταξινομημένα μέρη σε ένα μεγάλο πίνακα. Σε ψευδοκώδικα:
def mergeSort( A, n ):
if n = 1:
return A # it is already sorted
middle = floor( n / 2 )
leftHalf = A[ 1...middle ]
rightHalf = A[ ( middle + 1 )...n ]
return merge( mergeSort( leftHalf, middle ), mergeSort( rightHalf, n - middle ) )
Αυτή η συνάρτηση είναι πιο δύσκολη στην κατανόηση από όλες όσες έχουμε δει μέχρι τώρα, οπότε η παρακάτω άσκηση ίσως σας πάρει μερικά λεπτά.
Άσκηση 10
Επιβεβαιώστε την ορθότητα της mergeSort. Δηλαδή, ελέγξτε ότι η mergeSort όπως ορίζεται παραπάνω στην πραγματικότητα ταξινομεί σωστά τον πίνακα που της δόθηκε. Αν δυσκολεύεστε να καταλάβετε πώς δουλεύει, δοκιμάστε την με ένα απλό πίνακα ως παράδειγμα και τρέξτε την "στο χέρι". Όταν τρέχετε αυτή τη συνάρτηση στο χέρι, σιγουρευτείτε ότι τα leftHalf και rightHalf είναι μέρη που προκύπτουν αν κόψετε τον πίνακα κάπου στη μέση· δε χρειάζεται να είναι ακριβώς στη μέση αν ο πίνακας έχει περιττό πλήθος στοιχείων (αυτός είναι ο λόγος που εδώ χρησιμοποιείται η floor).
Ως τελευταίο παράδειγμα, ας αναλύσουμε την πολυπλοκότητα της mergeSort. Σε κάθε βήμα της mergeSort, χωρίζουμε τον πίνακα σε δύο μέρη ίσου μεγέθους, παρομοίως όπως κάναμε στην binarySearch. Εντούτοις, σε αυτή την περίπτωση, διατηρούμε και τα δύο μέρη κατά την εκτέλεση. Στη συνέχεια εφαρμόζουμε τον αλγόριθμο αναδρομικά και στα δύο μέρη. Όταν η αναδρομή επιστρέψει, εφαρμόζουμε τη διαδικασία merge στο αποτέλεσμα, η οποία παίρνει χρόνο Θ( n ).
Συνεπώς, χωρίζουμε τον αρχικό πίνακα σε δύο πίνακες που έχουν μέγεθος n / 2 ο καθένας. Στη συνέχεια συγχωνεύουμε αυτά τα μέρη, μία διαδικασία που συγχωνεύει n στοιχεία και άρα χρειάζεται Θ( n ) χρόνο.
Ρίξτε μια ματιά στην Εικόνα 7 για να καταλάβετε αυτή την αναδρομή.
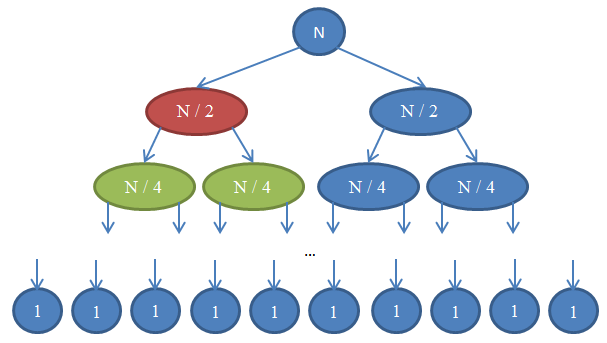
Ας δούμε τι συμβαίνει εδώ. Κάθε κύκλος αναπαριστά μία κλήση στη συνάρτηση mergeSort. Ο αριθμός μέσα στον κύκλο δείχνει το μέγεθος του πίνακα που ταξινομείται. Ο πάνω μπλε κύκλος είναι η αρχική κλήση στην mergeSort, όπου μας ζητείται να ταξινομήσουμε ένα πίνακα μεγέθους n. Τα βέλη δείχνουν αναδρομικές κλήσεις ανάμεσα σε συναρτήσεις. Η αρχική κλήση στη mergeSort κάνει με τη σειρά της δύο κλήσεις στη mergeSort για δύο πίνακες, από τους οποίους ο καθένας έχει μέγεθος n / 2. Αυτό φαίνεται από τα δύο βέλη στο πάνω μέρος του σχήματος. Με τη σειρά τους, καθεμία από αυτές τις κλήσεις κάνει η ίδια δύο κλήσεις στη mergeSort για να ταξινομήσει δύο πίνακες που έχουν μεγέθους n / 4 ο καθένας, και ούτω καθεξής έως ότου φτάσουμε σε πίνακες μεγέθους 1. Αυτό το διάγραμμα λέγεται δέντρο αναδρομής, επειδή απεικονίζει πώς η αναδρομή συμπεριφέρεται και μοιάζει με δέντρο (η ρίζα βρίσκεται στο πάνω μέρος και τα φύλλα βρίσκονται στο κάτω μέρος, οπότε στην πραγματικότητα μοιάζει με ένα αντεστραμμένο δέντρο).
Παρατηρήστε πως σε κάθε γραμμή στο παραπάνω διάγραμμα, ο συνολικός αριθμός στοιχείων είναι n. Για να το δείτε αυτό, παρατηρήστε κάθε γραμμή ξεχωριστά. Η πρώτη γραμμή περιλαμβάνει μόνο μία κλήση στη mergeSort με ένα πίνακα μεγέθους n, οπότε ο συνολικός αριθμός στοιχείων είναι n. Η δεύτερη γραμμή έχει δύο κλήσεις στη mergeSort καθεμιά μεγέθους n / 2. Όμως n / 2 + n / 2 = n οπότε ξανά και σε αυτή τη γραμμή το συνολικό πλήθος στοιχείων είναι n. Στην τρίτη γραμμή, έχουμε 4 κλήσεις καθεμία από τις οποίες εφαρμόζεται σε ένα πίνακα μεγέθους n / 4, δίνοντας ένα συνολικό πλήθος στοιχείων ίσο με n / 4 + n / 4 + n / 4 + n / 4 = 4n / 4 = n. Συνεπώς και πάλι έχουμε n στοιχεία. Παρατηρήστε ότι σε κάθε γραμμή σε αυτό το διάγραμμα, αυτός που πραγματοποιεί την κλήση θα πρέπει να εφαρμόσει μία merge στα στοιχεία που του επιστρέφονται από τις συναρτήσεις που κάλεσε. Για παράδειγμα, ο κύκλος που φαίνεται στο διάγραμμα με κόκκινο χρώμα έχει να ταξινομήσει n / 2 στοιχεία. Για να το κάνει αυτό, χωρίζει τον πίνακα που έχει n / 2 στοιχεία σε δύο πίνακες με n / 4 στον καθένα, καλεί την mergeSort αναδρομικά για να τους ταξινομήσει (αυτές οι κλήσεις είναι οι κύκλοι που φαίνονται με πράσινο χρώμα), και στη συνέχεια τους συγχωνεύει μαζί. Αυτή η διαδικασία συγχώνευσης πρέπει να συγχωνεύσει n / 2 στοιχεία. Σε κάθε γραμμή στο δέντρο μας, ο συνολικός αριθμός στοιχείων που συγχωνεύονται είναι n. Στη γραμμή που μόλις εξετάσαμε, η συνάρτηση συγχωνεύει n / 2 στοιχεία και η συνάρτηση στα δεξιά της (που φαίνεται με μπλε χρώμα) έχει επίσης να συγχωνεύσει n / 2 δικά της στοιχεία. Αυτό σημαίνει ότι ο συνολικός αριθμός των στοιχείων που πρέπει να συγχωνευθούν στη γραμμή που κοιτάμε είναι n.
Με αυτό το επιχείρημα, η πολυπλοκότητα για κάθε γραμμή είναι Θ( n ). Ξέρουμε ότι ο συνολικός αριθμός γραμμών σε αυτό το διάγραμμα, που λέγεται και βάθος του δέντρου αναδρομής, θα είναι log( n ). Η λογική σε αυτό είναι ακριβώς η ίδια που χρησιμοποιήσαμε όταν αναλύσαμε την πολυπλοκότητα της δυαδικής αναζήτησης. Έχουμε log( n ) γραμμές και καθεμία από αυτές είναι Θ( n ), άρα η πολυπλοκότητα της mergeSort είναι Θ( n * log( n ) ). Αυτό είναι πολύ καλύτερο από το Θ( n2 ) που είναι αυτό που μας έδωσε η ταξινόμηση επιλογής (θυμηθείτε ότι το log( n ) είναι πολύ μικρότερο του n, κι έτσι το n * log( n ) είναι πολύ μικρότερο από το n * n = n2). Αν όλο αυτό σας φαίνεται περίπλοκο, μην ανησυχείτε: Δεν είναι εύκολο την πρώτη φορά που το βλέπει κανείς. Ξαναδείτε αυτή την ενότητα και ξαναδιαβάστε τα επιχειρήματα εδώ μέσα μόλις υλοποιήσετε την mergeSort στην αγαπημένη σας γλώσσα προγραμματισμού και επιβεβαιώσετε ότι δουλεύει.
Όπως είδατε σ᾽ αυτό το τελευταίο παράδειγμα, η ανάλυση πολυπλοκότητας μας επιτρέπει να συγκρίνουμε αλγορίθμους για να δούμε ποιος είναι καλύτερος. Κάτω από αυτές τις συνθήκες, μπορούμε πλέον να είμαστε αρκετά σίγουροι ότι η ταξινόμηση συγχώνευσης θα τα πάει καλύτερα από την ταξινόμηση επιλογής για μεγάλους πίνακες. Θα ήταν δύσκολο να βγάλουμε αυτό το συμπέρασμα αν δεν είχαμε το θεωρητικό υπόβαθρο της ανάλυσης αλγορίθμων που αναπτύξαμε. Στην πράξη, όντως οι αλγόριθμοι ταξινόμησης που χρησιμοποιούμε είναι Θ( n * log( n ) ). Για παράδειγμα, ο πυρήνας του Linux χρησιμοποιεί έναν αλγόριθμο ταξινόμησης που λέγεται ταξινόμηση σωρού, που έχει τον ίδιο χρόνο εκτέλεσης με την ταξινόμηση συγχώνευσης που εξερευνήσαμε εδώ, συγκεκριμένα Θ( n log( n ) ) και είναι επίσης βέλτιστος. Παρατηρήστε ότι δεν έχουμε αποδείξει πως αυτοί οι αλγόριθμοι ταξινόμησης είναι βέλτιστοι. Για να το κάνουμε αυτό θα χρειαστούμε ένα ελαφρώς πιο περίπλοκο μαθηματικό επιχείρημα, αλλά μπορείτε να κοιμάστε ήσυχοι: οι αλγόριθμοι αυτοί πραγματικά δεν μπορούν να γίνουν καλύτεροι από πλευράς πολυπλοκότητας.
Έχοντας ολοκληρώσει αυτό τον οδηγό, η διαίσθηση που έχετε αναπτύξει για την ανάλυση της πολυπλοκότητας αλγορίθμων θα πρέπει να μπορεί να σας βοηθήσει να σχεδιάζετε γρηγορότερους αλγορίθμους και να επικεντρώνετε τις προσπάθειές σας όταν βελτιστοποιείτε σε πράγματα που έχουν πραγματικά σημασία και όχι στα μικρά πράγματα που δεν έχουν σημασία, επιτρέποντάς σας να είστε πιο παραγωγικός. Επιπροσθέτως, η μαθηματική γλώσσα και οι συμβολισμοί που αναπτύξαμε σε αυτό το άρθρο όπως ο συμβολισμός big-O είναι χρήσιμα όταν επικοινωνείτε με άλλους μηχανικούς λογισμικού όταν θέλετε να επιχειρηματολογήσετε σχετικά με το χρόνο εκτέλεσης αλγορίθμων, οπότε ελπίζω να μπορείτε να το κάνετε χρησιμοποιώντας τις νέες σας γνώσεις.
Λίγα λόγια
Αυτό το άρθρο χρησιμοποιεί την άδεια χρήσης Creative Commons 3.0 Attribution. Αυτό σημαίνει ότι μπορείτε να το αντιγράψετε και να το βάλετε όπου θέλετε, να το μοιραστείτε, να το βάλετε στη δική σας σελίδα, να το αλλάξετε, και γενικά να του κάνετε ό,τι θέλετε, υπό την προϋπόθεση ότι αναφέρετε το όνομά μου. Αν και δεν είστε υποχρεωμένος να κάνετε κάτι τέτοιο, αν χρησιμοποιήσετε τη δουλειά μου σας προτρέπω να χρησιμοποιήσετε επίσης Creative Commons έτσι ώστε να είναι ευκολότερο για τους άλλους να μοιράζονται και να συνεργάζονται και αυτοί. Παρομοίως, πρέπει κι εγώ να αναφέρω ποιες δουλειές ανθρώπων χρησιμοποίησα εδώ. Τα φίνα εικονίδια που βλέπετε σ᾽ αυτή τη σελίδα είναι τα fugue icons. Το πανέμορφο μοτίβο με τις πλάγιες γραμμές στο σχεδιασμό αυτής της σελίδας είναι της Lea Verou. Και, σημαντικότερα, τους αλγόριθμους που ξέρω έτσι ώστε να μπορέσω να γράψω αυτό το άρθρο μου τους δίδαξαν οι καθηγητές μου Νίκος Παπασπύρου και Δημήτρης Φωτάκης.
Αυτή τη στιγμή είμαι διδακτορικός φοιτητής κρυπτογραφίας στο Πανεπιστήμιο Αθηνών, ενώ αυτό το άρθρο το έγραψα ως προπτυχιακός φοιτητής Ηλεκτρολόγος Μηχανικός και Μηχανικός Υπολογιστών στο Εθνικό Μετσόβιο Πολυτεχνείο όπου ειδικεύτηκα στο λογισμικό και προπονητής στον Πανελλήνιο Διαγωνισμό Πληροφορικής. Όσο αφορά τη βιομηχανία έχω δουλέψει ως μέλος της ομάδας μηχανικών που έφτιαξαν το deviantART, ένα κοινωνικό δίκτυο για καλλιτέχνες, στις ομάδες ασφάλειας της Google και του Twitter, και δύο εταιρίες start-up, το Zino και την Kamibu όπου ασχοληθήκαμε με τους τομείς της κοινωνικής δικτύωσης και της κατασκευής βιντεοπαιχνιδιών αντίστοιχα. Ακολουθήστε με στο Twitter ή στο GitHub αν σας άρεσε το κείμενό μου, ή στείλ᾽ τε μου mail αν θέλετε να έρθετε σε επαφή μαζί μου. Πολλοί νεαροί προγραμματιστές δεν έχουν καλή γνώση της Αγγλικής γλώσσας. Στείλ᾽ τε μου e-mail αν θέλετε να μεταφράσετε αυτό το άρθρο στη μητρική σας γλώσσα έτσι ώστε περισσότεροι άνθρωποι να μπορέσουν να το διαβάσουν.
Ευχαριστώ που με διαβάσατε. Δεν πληρώθηκα για να γράψω αυτό το άρθρο, οπότε αν σας άρεσε, στείλτε μου ένα e-mail και πείτε μου ένα γεια. Μ᾽ αρέσει να μου στέλνουν φωτογραφίες από μέρη του κόσμου (και της Ελλάδας), οπότε μπορείτε να επισυνάψετε μία φωτογραφία σας στην περιοχή σας!
Αναφορές
- Cormen, Leiserson, Rivest, Stein. Εισαγωγή στους Αλγορίθμους, MIT Press.
- Dasgupta, Παπαδημητρίου, Vazirani. Αλγόριθμοι, McGraw-Hill Press.
- Φωτάκης. Μάθημα Διακριτών Μαθηματικών στο Εθνικό Μετσόβιο Πολυτεχνείο.
- Φωτάκης. Μάθημα Αλγορίθμων και Πολυπλοκότητας στο Εθνικό Μετσόβιο Πολυτεχνείο.

