Una Amable Introducción al Análisis de Complejidad de Algoritmos
Dionysis "dionyziz" Zindros <dionyziz@gmail.com>Maria Ramos <mariar@webhostinghub.com> — webhostinghub.com
- English
- Ελληνικά
- македонски
- Español
- Nederlands
- עברית
- Português
- srpskohrvatski
- Українська
- Русский
- Help translate
Introducción
Hoy en día, varios de los programadores que hacen un excelente y muy útil software, tal como la mayoría del software que vemos en Internet o usamos diariamente, no tienen una base teórica en ciencias computacionales. Aún así, crean programas bastante creativos y asombrosos, y les agradecemos que así lo hagan.
No obstante, la teoría de la ciencia computacional tiene aplicaciones que pueden resultar muy prácticas. En este artículo, dirigido a programadores que conocen su oficio, pero que no tienen conocimientos teóricos en ciencia computacional, presentaré una de las herramientas de mayor valor práctico de la ciencia computacional: la notación "Big-O" y el análisis de complejidad de algoritmos. Como alguien que tiene experiencia tanto en la academia de la ciencia computacional, como en la creación de software de producción para la industria, me he encontrado con que esta es la herramienta que en la práctica resulta ser la más útil, por lo que espero que después de que haya leído este artículo, la pueda aplicar para mejorar sus propios códigos. Después de leer este post, usted entenderá términos que los científicos computacionales utilizan comúnmente, tales como "Big-O", "asymptotic behavior" y "worst-case analysis", los cuales definiremos más adelante.
Este texto también está dirigido a estudiantes de escuela secundaria de Grecia o de cualquier otro lugar, que estén compitiendo en las Olimpiadas Internacionales en Informática, alguna competición en algoritmos, para estudiantes, o cualquier competición similar. Como tal, no tiene prerrequisitos matemáticos y le dará una base teórica que le permitirá continuar el estudio de algoritmos con un sólido entendimiento de la teoría que los sustenta. Siendo alguien que ha competido en estos certámenes, le recomiendo enfáticamente que lea todo este material introductorio y trate de entenderlo completamente, ya que será necesario para sus estudios de algoritmos y para aprender técnicas más avanzadas.
También creo que este texto será de utilidad para programadores industriales que no tienen mayor experiencia en la teoría de la ciencia computacional (es un hecho que algunos de los ingenieros de software más talentosos nunca fueron a la universidad). Pero debido a que también es para estudiantes, es posible que a ratos parezca un texto pedagógico. Además, algunos de los temas en este texto puede que le parezcan algo obvios; es posible que haya estudiado varios de ellos durante su paso por la secundaria. Si siente que los entiende bien, puede omitirlos. Otras secciones tienen mayor complejidad y se vuelven levemente teóricas, ya que los estudiantes que participan en estas competiciones necesitan saber más acerca de algoritmos teóricos en comparación con un practicante promedio. Sin embargo, no está de más saber estas cosas y no son complicadas de asimilar, por lo que ciertamente vale la pena dedicarles un tiempo. Debido a que el texto original estaba dirigido a estudiantes de secundaria, no es necesaria una base en matemática, por lo que cualquiera con experiencia en programación (i.e. si sabe que es la recursión) podrá avanzar sin problema.
A través de este artículo encontrará varios indicadores que dirigen a material de interés, generalmente fuera del alcance del tópico en discusión. Si usted es un programador industrial, es muy probable que esté familiarizado con varios de estos conceptos. Por otro lado, si usted es un estudiante junior que participa en competiciones, el seguir estos enlaces le dará pistas de otras áreas de la ciencia computacional o de la ingeniería de software que podría no haber explorado aún y que le permitirán ampliar sus intereses.
La notación "Big-O" y el análisis de complejidad de algoritmos es algo que muchos programadores industriales y estudiantes junior consideran complejo de entender, le temen, o lo evitan por verlo como algo inútil. Sin embargo, no es algo tan difícil ni teórico como puede parecer en un comienzo. La complejidad de algoritmo es simplemente una forma de evaluar qué tan rápido un programa o un algoritmo se ejecutan, así que, en realidad, es algo bastante pragmático. Partamos motivando el tema un poco.

Motivación
Ya sabemos que existen herramientas que permiten medir qué tan rápido un programa está corriendo. Existen programas llamados profilers los cuales miden el tiempo de ejecución en milisegundos y nos ayudan a optimizar nuestro código, al identificar los cuellos de botella que podría haber en él. Si bien esta es una herramienta útil, no es de particular importancia para la complejidad de algoritmo. La complejidad de algoritmo está diseñada para comparar dos algoritmos en un nivel conceptual, de idea – ignorando los detalles de su puesta en marcha, tales como su implementación en un lenguaje de programación, el algoritmo de hardware en el que se ejecuta, o el set de instrucciones dados a la CPU. Lo que nos interesa es comparar los algoritmos en base a lo que son: Ideas de cómo algo es computado. Contar los milisegundos no nos colaborará en eso. Es muy posible que un algoritmo pobre, escrito en un lenguaje básico tal como Assembly se ejecute mucho más rápido que un buen algoritmo escrito en un lenguaje avanzado tales como el Python o el Ruby. Por lo tanto, es momento de definir que es realmente un "mejor algoritmo".
Debido a que los algoritmos son programas que lo que hacen es simplemente computar, y no otras cosas que los computadores suelen hacer, tales como tareas de networking o gestionar inputs y outputs del usuario, el análisis de complejidad nos permitirá medir que tan rápido se desempeña un programa mientras realiza cómputos. Ejemplos de operaciones que son netamente computacionales incluyen las floating-point operations u "operaciones de punto flotante", tales como son la adición o la multiplicación; búsquedas en bases de datos que encajan en RAM para un valor dado; la determinación de una ruta para que un personaje de inteligencia artificial siga en un videojuego, de modo de que tenga que caminar distancias cortas en un mundo virtual (ver Figura 1); o ejecutar un patrón de expresión regular que encaje en un string. Claramente, la computación es algo ubicuo en los programas computacionales.
El análisis de complejidad también es una herramienta que nos permite explicar cómo un algoritmo se comporta a medida de que el input se acrecenta. Si ingresamos un input diferente, ¿cómo responderá el algoritmo? Si nuestro algoritmo se demora 1 segundo en correr para un input de tamaño 1000, ¿cómo se comportará si duplicamos el input? ¿Correrá igual de rápido, a la mitad de rápido, o cuatro veces más lento? En la programación práctica, esto es de importancia, ya que nos permitirá predecir cómo se comportará nuestro algoritmo cuando la cantidad de información ingresada sea mayor. Por ejemplo, si hacemos un algoritmo para una aplicación web que opera bien con 1000 usuarios y que mide su tiempo de ejecución, usando el análisis de complejidad de algoritmo podremos tener una idea bastante clara de qué ocurrirá cuando tengamos 2000 usuarios. Para competiciones de algoritmos, el análisis de complejidad nos dará una percepción de cuánto tiempo correrá nuestro código en los casos de prueba más grandes, y que se usan para medir la exactitud de nuestro programa. De este modo, si hemos evaluado el comportamiento de nuestro programa para un input pequeño, podemos tener una buena idea de cómo operará con inputs mayores. Comencemos con un ejemplo sencillo: Encontrar el elemento máximo de un array.
Instrucciones de Conteo
En este artículo usaré varios lenguajes de programación para los ejemplos. Sin embargo, no desespere si no conoce alguno de estos lenguajes. Gracias a que usted sabe de programación, podrá leer los ejemplos sin problemas, incluso si no es familiar con el lenguaje de programación que esté siendo utilizado, ya que los ejemplos serán sencillos y sin funciones avanzadas o esotéricas. Si usted es un estudiante participante de competiciones de algoritmos, lo más seguro es que trabaje con C++, por lo que no tendrá dificultades en seguir el texto. En este caso, recomiendo el uso de C++ para practicar en los ejercicios.
El elemento máximo en un array puede encontrarse usando este sencillo trozo de código de Javascript. Dado como input un array Ade tamaño n:
var M = A[ 0 ];
for ( var i = 0; i < n; ++i ) {
if ( A[ i ] >= M ) {
M = A[ i ];
}
}
Luego, lo primero que haremos es contar cuantas instrucciones fundamentales ejecuta este trozo de código. Haremos esto sólo una vez, y no será necesario mientras desarrollemos nuestra teoría, así que ténganme un poco de paciencia mientras lo realizamos. A medida que analizamos este trozo de código, querremos dividirlo en pequeñas instrucciones sencillas; cosas que puedan ser ejecutadas directamente por la CPU, o al menos cerca de eso. Asumiremos que nuestro procesador puede ejecutar las siguientes instrucciones por separado:
- Asignar un valor a una variable
- Buscar el valor de un elemento en particular en un array
- Comparar dos valores
- Incrementar un valor
- Operaciones aritméticas básicas tales como adición y multiplicación
Asumiremos que la bifurcación (la elección entre las partes if y else del código, luego de que la condición if ha sido evaluada) ocurre instantáneamente y no considerará estas instrucciones. En el código anterior, la primera línea es:
var M = A[ 0 ];
Esto requiere 2 instrucciones: una para buscar A[ 0 ]y otra para asignar el valor a M (asumimos que n siempre es al menos 1). Estas dos instrucciones siempre son requeridas por el algoritmo, independiente del valor de n. El código de iniciación de bucle o for loop también tiene que correr siempre. Esto nos da dos instrucciones más: una assignment o asignación y una comparison o comparación:
i = 0;
i < n;
Estas correrán antes de la primera iteración for loop. Después de cada iteración for loop, necesitaremos ejecutar dos instrucciones más: un incremento de i y una comparación para chequear si nos mantenemos en el bucle:
++i;
i < n;
Entonces, si ignoramos el cuerpo del bucle, el número de instrucciones que necesita este algoritmo son 4 + 2n. Esto es, 4 instrucciones al comienzo del forloop y dos instrucciones al final de cada iteración de la que obtenemos n. Ahora, podemos definir una función f( n ), la cual, dado un n,nos entrega el número de instrucciones que el algoritmo necesita. Para un cuerpo for vacío tenemos f( n ) = 4 + 2n.
Análisis Worst-Case o del Peor Caso
Ahora, si nos fijamos en el cuerpo del for tenemos una operación de búsqueda en array y una comparación que ocurre siempre:
if ( A[ i ] >= M ) { ...
Eso serían dos instrucciones. Pero el cuerpo del if podría correr o no correr, dependiendo de cuáles son los valores del array. Si ocurriese que A[ i ] >= M, ntonces ejecutaremos dos instrucciones adicionales – una búsqueda en array y una asignación:
M = A[ i ]
Pero ahora no podemos definir una f(n) tan fácilmente, porque nuestra cantidad de instrucciones no depende solamente de n sino que también de nuestro input. Por ejemplo, para A = [ 1, 2, 3, 4 ] el algoritmo necesitará más instrucciones que para A = [ 4, 3, 2, 1 ]. Al analizar algoritmos, generalmente consideramos el peor escenario. ¿Qué es lo peor que puede ocurrir con nuestro algoritmo? ¿En qué caso nuestro algoritmo requiere la mayor cantidad de instrucciones para correr? En este caso, es cuando tenemos un array en orden ascendente del tipo A = [ 1, 2, 3, 4 ]. En este caso, M necesita ser reemplazado cada vez y entonces eso entrega la mayor cantidad de instrucciones. Los científicos computacionales usan un vistoso término para referirse a esto y lo llaman "worst-case analysis" o análisis del peor escenario. Esto no es nada más que considerar el escenario en que tenemos más mala suerte. Entonces, en el peor de los casos, tenemos 4 instrucciones para ejecutar dentro del cuerpo del for por lo que tenemos f( n ) = 4 + 2n + 4n = 6n + 4. Esta función f, dado un tamaño n del problema, entrega el número de instrucciones que serían necesarias en el peor de los casos.
Asymptotic Behavior o Comportamiento Asintótico
Dada una función semejante, tenemos una idea bastante clara de qué tan rápido es un algoritmo. Sin embargo, como les prometí, no será necesario realizar la tediosa tarea de contar instrucciones en nuestro programa. Además, la cantidad real de instrucciones de la CPU requeridas para cada enunciado del lenguaje de programación depende del compilador y de nuestro lenguaje de programación, así como también del set de instrucciones disponibles de la CPU (i.e. ya se trate de un AMD o de un Intel Pentium, o de un procesador MIPS o de su Playstation 2), y dijimos que eso lo ignoraríamos. Ahora ejecutaremos nuestra función "f" a través de un "filtro" que nos ayudará a deshacernos de esos detalles menores que los científicos computacionales prefieren omitir.
En nuestra función, 6n + 4, tenemos dos términos: 6n y 4. En análisis de complejidad solamente nos preocupamos de lo que ocurre con la función contadora de instrucciones a medida que crece el input (n) del programa. Esto en realidad va en paralelo con las ideas previas del comportamiento en el peor escenario: estamos interesados en cómo se comporta nuestro algoritmo cuando se le trata de forma ruda; cuando se le reta a hacer algo difícil. Note que esto es bastante útil cuando estamos comparando algoritmos. Si un algoritmo derrota a otro algoritmo frente a un gran input, lo más cierto será que el algoritmo más rápido seguirá siéndolo cuando se le ingrese un input más simple y pequeño. De los términos que estamos considerando, haremos a un lado todos aquellos que crecen lentamente y sólo mantendremos los que crecen rápidamente, a medida que n se hace mayor. Claramente un 4 sigue como un 4 n crece, pero 6n aumenta y aumenta, por lo su influencia crecerá de igual forma en problemas de mayor tamaño. Por esto, lo primero que haremos será eliminar el 4 y dejaremos la función como f( n ) = 6n.
Si lo piensa, esto tiene sentido, ya que el 4 es simplemente una constante de iniciación. Diferentes lenguajes de programación requerirán distintos tiempos para ponerse en marcha. Por ejemplo, Java requiere inicializar su máquina virtual. Ya que estamos ignorando diferencias en el lenguaje de programación, será lógico ignorar este término.
El segundo aspecto que ignoraremos será la constante que multiplica a n, por lo que nuestra función quedará en f( n ) = n. Como puede ver esto simplifica bastante las cosas. De nuevo, tiene sentido eliminar esta constante de multiplicación si tenemos en cuenta como compilan los diferentes lenguajes de programación. La sentencia "array lookup" en un lenguaje puede compilar instrucciones distintas dependiendo del lenguaje. Por ejemplo, en C, hacer A[ i ]no contempla un chequeo de que i esté dentro del array declarado, mientras que Pascal sí lo hace. Es así como el siguiente código Pascal:
M := A[ i ]
Es equivalente al siguiente en C:
if ( i >= 0 && i < n ) {
M = A[ i ];
}
Por esto, es razonable esperar que distintos lenguajes de programación entreguen diferentes factores cuando contabilizamos sus instrucciones. En nuestro ejemplo, en el que estamos usando un compilador torpe para Pascal, el que además es inconsciente de posibles optimizaciones, Pascal requiere 3 instrucciones por cada acceso denegado a un array en vez de 1 instrucción, como C requiere. Dejar este factor de lado es coherente con ignorar las diferencias particulares entre uno y otro lenguaje de programación y compiladores, y enfocarse solamente en la idea del algoritmo mismo.
Este filtro de "eliminar todos los factores" y de "mantener el término de mayor crecimiento", como describimos anteriormente, es lo que denominamos asymptotic behavior. Entonces el comportamiento asintótico de f( n ) = 2n + 8 es descrito por la función f( n ) = n. Matemáticamente halando, lo que estamos diciendo es que lo que nos interesa es el límite de la función n a medida que tiende al infinito. Si no entiende que es lo que formalmente significa esa frase, no se preocupe, ya que esto es todo lo que necesita saber. (Como nota al margen, en un contexto estrictamente matemático, no podríamos eliminar las constantes en el límite, pero considerando los objetivos de las ciencias computacionales, sí lo querremos hacer, por las razones antes expuestas). Tomemos un par de ejemplos para familiarizarnos con el concepto.
Encontremos el comportamiento asintótico de las siguientes funciones, mediante la eliminación de los factores constantes y manteniendo los términos que crecen más rápido.
f( n ) = 5n + 12 queda en f( n ) = n.
Usando el mismo razonamiento
f( n ) = 109 queda en f( n ) = 1.
Estamos eliminando el multiplicador 109*1, pero todavía tenemos que poner un 1, para indicar que esta función tiene un valor distinto de 0.
f( n ) = n2 + 3n + 112 queda en f( n ) = n2
Aquí, n2 crece más rápido que 3n, para un n suficientemente grande, asique sólo mantenemos n2.
f( n ) = n3 + 1999n + 1337 queda en f( n ) = n3
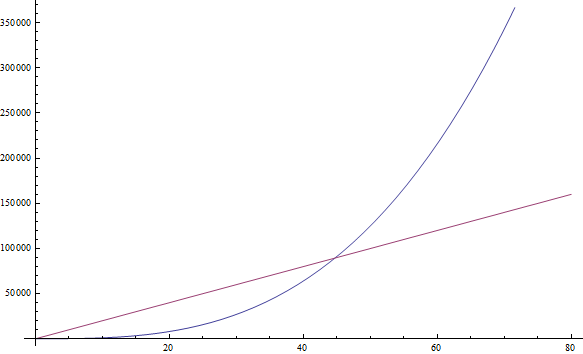
Aunque el factor en frente de n es bastante grande, aún podemos encontrar un n suficientemente grande de modo de que n3 sea mayor que 1999n. Como sólo estamos interesados en el comportamiento de valores muy grandes de n, sólo mantenemos n3 (Ver Figura 2).
f( n ) = n +
 queda en f( n ) = n
queda en f( n ) = nEsto es porque n crece más rápido que
 a medida que incrementamos n.
a medida que incrementamos n.
YTrate usted mismo con los siguientes ejemplos:
Ejercicio 1
- f( n ) = n6 + 3n
- f( n ) = 2n + 12
- f( n ) = 3n + 2n
- f( n ) = nn + n
(Escriba sus resultados; la solución se entrega a continuación)
Si tiene algún problema, pruebe reemplazando algún n muy grande y compruebe qué término es mayor. Bastante directo, ¿no?
Complejidad
En síntesis, lo que se nos está diciendo es que como podemos eliminar todas estas constantes ornamentales, es bastante sencillo identificar el comportamiento asintótico de una función contadora-de-instrucciones de un programa. De hecho, cualquier programa que carezca de bucles tendrá una f(n) = 1, ya que el número de instrucciones que requiere es simplemente una constante (a menos que utilice recursión; ver a continuación). Cualquier programa con un único bucle que vaya desde 1 a n tendrá f(n) = n, ya que ejecutará un número fijo de instrucciones antes del bucle, un número fijo de instrucciones después del bucle y un número constante de instrucciones dentro del bucle que corre n veces.
Ahora esto tendría que ser mucho más fácil y menos tedioso que contar instrucciones individuales, así que demos una mirada a un par de ejemplos para familiarizarnos con esto. El siguiente programa PHP chequea si existe un valor particular dentro de un array A de tamaño n:
<?php
$exists = false;
for ( $i = 0; $i < n; ++$i ) {
if ( $A[ $i ] == $value ) {
$exists = true;
break;
}
}
?>
Este método de búsqueda de un valor dentro de un array se denomina "linear search" o "búsqueda lineal". Este es un nombre razonable, ya que este programa tiene a f( n ) = n (en la siguiente sección definiremos que significa exactamente "lineal"). Puede haberse percatado de que existe un enunciado de "quiebre" que puede ocasionar que el programa finalice prematuramente, incluso después de una única iteración. Pero recuerde que estamos interesados en el peor escenario, el cual, para este programa, será cuando el array A no contenga el valor. Así que aún tenemos f( n ) = n.
Ejercicio 2
Analice sistemáticamente el número de instrucciones que en el peor caso el programa PHP anterior necesita con respecto a n para hallar f(n). Hágalo de forma similar a como analizamos nuestro primer programa Javascript. Luego, compruebe que, asintóticamente, tenemos f(n)=n.
Demos una mirada a un programa Python que suma dos elementos de un array para producir una suma que se almacena en otra variable:
v = a[ 0 ] + a[ 1 ]
Aquí tenemos una cantidad constante de instrucciones, por lo que tenemos que f( n ) = 1.
El siguiente programa en C++ chequea si es que un vector (un sofisticado tipo de array) denominado A y de tamaño ncontiene los mismos dos valores en cualquier lugar dentro de él.
bool duplicate = false;
for ( int i = 0; i < n; ++i ) {
for ( int j = 0; j < n; ++j ) {
if ( i != j && A[ i ] == A[ j ] ) {
duplicate = true;
break;
}
}
if ( duplicate ) {
break;
}
}
Como aquí tenemos dos bucles anidados entre sí, tendremos un comportamiento asintótico descrito por f( n ) = n2.
Regla General: S El análisis de programas sencillos se puede hacer contando los bucles anidados que contiene el programa. Un sólo bucle sobre n ítems genera f(n)=n. Un bucle dentro de otro bucle f( n ) = n2. Un bucle dentro de un bucle que está dentro de otro bucle genera f( n ) = n3.
Si tenemos un programa que invoca una función dentro de un bucle, y sabemos el número de instrucciones que la función invocada realiza, entonces es fácil determinar el número de instrucciones de todo el programa. De hecho, demos una mirada al siguiente ejemplo en C:
int i;
for ( i = 0; i < n; ++i ) {
f( n );
}
Si sabemos que f( n ) es una función que realiza exactamente n
funciones, entonces podremos saber que asintóticamente la cantidad de instrucciones de todo el programa es n2,
ya que la función es invocada exactamente n veces.
Regla General: Dado un conjunto de bucles que son secuenciales, el más lento de ellos determina el comportamiento asintótico del programa. Dos bucles anidados, seguidos por un solo bucle, asintóticamente es lo mismo que los bucles anidados por sí solos, ya que los bucles anidados dominan el bucle individual.
Ahora, enfoquémonos en la sofisticada notación que los científicos computacionales utilizan. Cuando hayamos encontrado la f asintótica exacta, diremos que nuestro programa es Θ( f( n ) ). Por ejemplo, los programas anteriores son Θ( 1 ), Θ( n2 ) y Θ( n2 ) respectivamente. Θ( n ) se pronuncia "theta de n". A veces diremos que f( n ), la función original que cuenta las instrucciones que incluyen las constantes es Θ( algo ). Por ejemplo, podremos decir que f( n ) = 2n es una función que es Θ( n ) - nada nuevo en esto. También podremos escribir 2n ∈ Θ( n ), lo cual se pronuncia " dos n es theta de n". No se confunda con esta notación: Todo lo que está diciendo es que si hemos contados el número de instrucciones que un programa requiere y que si esa cantidad es 2n, entonces el comportamiento asintótico de nuestro algoritmo es descrito por n, a lo cual llegamos al eliminar las constantes. Dada esta notación, los siguientes son algunos enunciados puramente matemáticos.
- n6 + 3n ∈ Θ( n6 )
- 2n + 12 ∈ Θ( 2n )
- 3n + 2n ∈ Θ( 3n )
- nn + n ∈ Θ( nn )
A propósito, si resolvió el Ejercicio 1, estas son exactamente las respuestas que debería haber encontrado.
Llamamos esta función, esto es, lo que colocamos dentro de Θ (aquí) como complejidad temporal, o simplemente complejidad de nuestro algoritmo. Entonces, un algoritmo con Θ( n ) es de complejidad n. También tenemos nombres especiales para Θ( 1 ), Θ( n ), Θ( n2 ) y Θ( log( n ) ) ya que aparecen bastante seguido. Decimos que un algoritmo Θ( 1 ) es un algoritmo temporalmente-constante, Θ( n ) es linear, θ( n2 ) es cuadrático y Θ( log( n ) ) es logarítmico (no se preocupe si todavía no sabe que son los logaritmos, llegaremos a eso dentro de poco).
Regla general: Programas con un Θ mayor corren más lentamente que programas con un Θ menor.

Notación Big-O u O-Grande
Ahora, a veces es cierto que será más difícil dilucidar mediante este método, como hicimos anteriormente, el comportamiento exacto de un algoritmo, especialmente en casos más complejos. Sin embargo, podremos decir que el comportamiento de nuestro algoritmo nunca traspasará una cierta frontera. Esto nos facilitará la vida, ya que no tendremos que especificar cabalmente qué tan rápido corre nuestro algoritmo, incluso si ignoramos las constantes, como hicimos anteriormente. Todo lo que tendremos que hacer es encontrar una cierta frontera, o límite. Esto se explica fácilmente con un ejemplo.
Un conocido problema que los científicos computacionales usan para enseñar algoritmos es el problema de ordenación. En este problema, un array de tamaño A nos n algoritmos es el problema de ordenación. En este problema, un array de tamaño A nos es dado (¿le suena familiar?) y se nos pide que escribamos un programa que ordene este array. El problema es interesante porque es un caso común en sistemas reales. Por ejemplo, un explorador de archivos necesita ordenar los archivos que muestra de acuerdo a su nombre, de modo de que el usuario pueda navegar en ellos con facilidad. O en otro caso, un video juego necesita ordenar los objetos 3d que muestra, basándose en la distancia que los separa del ojo del jugador dentro de este mundo virtual. Esto sirve para determinar qué es visible y qué no lo es, algo llamado Problema de Visibilidad (ver Figura 3). Los objetos que resultan ser los más cercanos al jugador pasan a ser los visibles, mientras que aquellos que están más lejanos podrían quedar escondidos por los objetos que tienen en frente. El ordenamiento también es algo interesante porque existen muchos algoritmos que lo realizan, algunos peores que otros. También es un problema sencillo de definir y explicar. Por lo tanto, escribamos un trozo de código que ordene un array.
Aquí tenemos una ineficiente manera de implementar el ordenamiento de un array usando Ruby. (Por supuesto, Ruby permite ordenar arrays usando funciones que tiene incorporadas, cuyo uso es preferible, y las cuales son claramente más rápidas de lo que veremos en este ejemplo, el cual es sólo con propósitos ilustrativos).
b = []
n.times do
m = a[ 0 ]
mi = 0
a.each_with_index do |element, i|
if element < m
m = element
mi = i
end
end
a.delete_at( mi )
b << m
end
Este método se denomina "selection sort".
u "ordenamiento por selección". Encuentra el mínimo de nuestro array (el array es denotado a
como antes, mientras que el valor mínimo se denota m y mi
es su índice), lo coloca al final de un nuevo array (en nuestro caso b),
y lo retira del array original. Luego, encuentra el mínimo de entre los valores restantes en el array original, lo añade a nuestro nuevo array, el cual ahora contiene dos elementos, y lo remueve de nuestro array inicial. Continúa este proceso hasta que se han sacado todos los ítems del array original y han sido insertados en el nuevo array. Esto significa que el array ha sido ordenado. En este ejemplo, nos damos cuenta de que tenemos dos bucles anidados. El bucle exterior corre
n veces, y el bucle interior corre una vez por cada elemento del array
a. Mientras el array a inicialmente tiene n
elementos, le removemos un ítem en cada iteración. Es así como el bucle interior se repite n
veces durante la primera iteración de nuestro bucle exterior, y luego n - 1 veces, luego n - 2
veces y así sucesivamente, hasta que la última iteración del bucle externo, en la cual sólo corre una vez.
.
Es algo más difícil evaluar la complejidad de este programa, ya que tenemos que resolver la suma 1 + 2 + … + (n - 1) + n. Pero lo que ciertamente si le podemos hallar es un "límite superior". Esto es, podemos modificar nuestro programa (puede hacerlo mentalmente, no en el código mismo) para hacerlo peor de lo que es y luego encontrar la complejidad de este nuevo programa que generamos. Si podemos encontrar la complejidad del programa peor, entonces sabremos que nuestro programa original es como máximo así de malo, o mejor que eso. De esta forma, si encontramos una buena com plejidad en nuestro programa modificado, el cual es peor que el original, podremos saber que nuestro programa ori ginario también tendrá una complejidad bastante buena, tan buena como la del programa alterado, o incluso mejor.
Ahora bien, pensemos en una forma de editar este programa de ejemplo, con el propósito de que sea más fácil encontrar su complejidad. No obstante, tengamos en mente que sólo podemos empeorarlo, i.e., hacer que requiera más instrucciones, por lo que nuestra estimación será válida para el programa original. Claramente podemos modificar el bucle interno del programa para que siempre se repita exactamente n veces, en vez de una cantidad variable de veces. Algunas de estas repeticiones serán inútiles, pero nos permitirán analizar la complejidad del algoritmo resultante. Si hacemos este sencillo cambio, entonces el nuevo algoritmo que hemos hecho claramente es Θ( n2 ), porque tenemos dos bucles anidados, repitiéndose cada uno exactamente n veces. Si esto es así, diremos que el algoritmo original es O( n2 ). O( n2 ) se pronuncia "O-Grande de n cuadrado". Lo que esto nos dice es que asintóticamente nuestro programa no es peor que n2. Puede que sea mejor que eso, o quizá es igual que eso. Dicho sea de paso, si de hecho nuestro programa es Θ( n2 ), aún podemos decir que es O( n2 ). Para ayudarle a entenderlo, imagine que alteramos el programa original de un modo que no cambie tanto, pero que aún así lo hace algo peor. Por ejemplo podemos añadir instrucciones insignificantes al comienzo del programa. Haciendo esto alteraremos la función contadora-de-instrucciones mediante una simple constante, la cual se ignora en el comportamiento asintótico. Por esto, un programa que es Θ( n2 ) también será O( n2 ).
Pero, a la inversa, un programa que es O( n2 ) podría no ser Θ( n2 ).
Por ejemplo, cualquier programa que es Θ( n ) también es O( n2 )
además de ser O( n ). Si nos imaginamos que un programa Θ( n ) es un bucle sencillo for que se repite n
veces, podremos empeorarlo al envolverlo en otro bucle for que también se repita n
veces, generando así un programa con f( n ) = n2. Si generalizamos esto, cualquier programa que sea Θ( a ) es
O( b ) cuando b es peor que a.
Note que nuestra alteración al programa no tiene porqué darnos un programa que sea equivalente o comparable a nuestro programa original. Solamente tiene realizar más instrucciones que el original para un
n. dado, ya que simplemente lo estaremos usando para contar instrucciones, no para resolver nuestro problema concreto.
Por tanto, afirmar que nuestro programa es O( n2 ) es quedarse a resguardo: Hemos analizado nuestro algoritmo y hemos encontrado que nunca es peor que n2. Pero podría darse el caso de que de hecho sea n2. Esto nos entrega un buen estimativo de qué tan rápido corre nuestro programa. Revisemos algunos ejemplos que lea yudaránn a familiarizarse con esta nueva notación.
Ejercicio 3
Indique cual de los siguientes es verdadero:
- A Θ( n ) algoritmo O( n )
- A Θ( n ) algoritmo es O( n2 )
- A Θ( n2 ) algorithm is O( n3 )
- A Θ( n ) algoritmo es O( 1 )
- A O( 1 ) algoritmo es Θ( 1 )
- A O( n ) algoritmo es Θ( 1 )
Solución
- Sabemos que esto es verdadero, ya que nuestro programa original era Θ( n ). Podemos obtener O( n ) sin alterar en absoluto nuestro programa.
- Como n2 es peor que n, es verdadero.
- Como n3 es peor que n2, es verdadero.
- Como 1 no es peor que n, es falso. Si un programa toma n nstrucciones asintóticamente (una cantidad lineal de instrucciones), no puede empeorarse, por lo que tomará sólo 1 instrucción asintóticamente (una cantidad constante de instrucciones).
- Verdadero, ya que ambas complejidades son iguales.
- Podría ser o no ser verdadero, dependiendo del algoritmo. En un caso genérico, será falso. Si un algoritmo es Θ( 1 ), entonces ciertamente es O( n ). Pero si es O( n ), podría no ser Θ( 1 ). Por ejemplo, un algoritmo Θ( n ) es O( n ) pero no Θ( 1 ).
Ejercicio 4
Utilice una suma de progresión aritmética para probar que el programa anterior no es solamente O( n2 ) sino que también es Θ( n2 ). Si no sabe que es una progresión aritmética, búsquelo en Wikipedia – es algo sencillo.
Debido a que la complejidad-O de un algoritmo entrega un límite superior para la complejidad real de un algoritmo, mientras que Θ entrega la complejidad real de un algoritmo, a veces decimos que Θ entrega un límite ajustado. Si sabemos que hemos encontrado un límite de complejidad que no es ajustado, podemos denotarlo con minúsculas. Por ejemplo, si un algoritmo es Θ( n ), entonces su complejidad ajustada es n. Por tanto, este algoritmo es tanto O( n ) como O( n2 ). Como el algoritmo es Θ( n ), O( n ) tiene un límite ajustado. Pero el límite de O( n2 ) no es ajustado, por lo que podemos escribir el algoritmo como o( n2 ), lo cual se pronuncia "o pequeña de n cuadrada", para denotar que sabemos que nuestro límite no es ajustado. Aunque no siempre es algo fácil de hacer, es mejor encontrar los límites ajustados de nuestros algoritmos, ya que estos nos entregan mayor información acerca del comportamiento del algoritmo.
Ejercicio 5
Determine cuál de los siguientes límites son límites ajustados y cuáles no lo son. Revise si hay límites erróneos. Use o( notación ) para denotar los límites que no son ajustados.
- Un algoritmo Θ( n ) para el cual encontramos un límite superior O( n ).
- Un algoritmo Θ( n2 ) para el cual encontramos un límite superior O( n3 ).
- Un algoritmo Θ( 1 ) para el cual encontramos un límite superior O( n ).
- Un algoritmo Θ( n ) para el cual encontramos un límite superior O( 1 ).
- Un algoritmo Θ( n ) para el cual encontramos un límite superior O( 2n ).
Solución
- En este caso las complejidades de Θ y de O, son iguales, por lo que el límite es ajustado.
- Aquí vemos que la complejidad de O es de una mayor magnitud que la complejidad de Θ, por lo que este límite no es ajustado. De hecho, un límite de O( n2 ) sería de tipo ajustado. En consecuencia podemos escribir que el algoritmo es o( n3 ).
- Nuevamente, vemos que la complejidad de O es mayor que la complejidad de Θ, por lo que tenemos un límite que no es ajustado. Un límite de O( 1 ) sería de tipo ajustado. Por tanto, podemos indicar que el límite de O( n ) no es ajustado, escribiéndolo como o( n ). .
- Ciertamente hemos cometido un error al calcular este límite, ya que está errado. Es imposible que un algoritmo Θ( n ) tenga un límite superior de O( 1 ), ya que n es una complejidad mayor que 1. Recuerde que O entrega un límite superior.
- Este parece un límite no ajustado, pero en realidad no es así. De hecho se trata de un límite ajustado. Recuerde que el comportamiento asintótico es el mismo para 2n y n, y que O y Θ sólo están relacionados con el comportamiento asintótico. Entonces tenemos que O( 2n )= O( n ) y que por lo tanto este límite es ajustado, ya que la complejidad es la misma que Θ.
Regla General: Es más fácil encontrar la complejidad-O de un algoritmo que su complejidad-Θ.
Puede ser que en este momento se sienta algo abrumado con esta nueva notación, pero introduzcamos dos símbolos más, antes de pasar a algunos ejemplos. Estos serán sencillos de asimilar, ahora que ya conoce Θ, O y o, y no los usaremos hasta más avanzados en este artículo. Sin embargo es bueno que los presentemos ahora, ya que estamos en ello. En los ejemplos anteriores, modificamos nuestro programa para estropearlo deliberadamente (es decir, que requiera más instrucciones, y por lo tanto más tiempo) y creamos la notación O. O es relevante ya que nos indica que nuestro programa nunca será más lento que un determinado límite, y por lo tanto nos entrega información valiosa, con la que podemos defender la calidad de nuestro programa. Si hacemos lo opuesto, y modificamos nuestro programa para hacerlo mejor y encontramos la complejidad del nuevo programa, usamos la notación Ω. Luego, Ω nos indica una complejidad que sabemos nuestro programa nunca superará. Esto es útil si queremos probar que un programa corre lentamente o que un algoritmo es deficiente. Esto puede ser útil para sostener que un algoritmo es demasiado lento para un determinado propósito. Por ejemplo, decir que un algoritmo es Ω( n3 )indica que el algoritmo no es mejor que n3. Podría ser que Θ( n3 ),sea tan malo como Θ( n4 ) o incluso peor, pero sabemos que es al menos algo así de malo. Entonces, Ω nos entregará un límite inferior para la complejidad de nuestro algoritmo. Como en el caso de o, podemos escribir ω si sabemos que el límite no es ajustado. Por ejemplo, un algoritmo Θ( n3 ) es ο( n4 ) y ω( n2 ). Ω( n ) se pronuncia "omega grande de n", mientras que ω( n ) se pronuncia "omega pequeña de n".
Ejercicio 6
Para las siguientes complejidades Θ, escriba un límite O ajustado y no ajustado y un límite Ω ajustado y no ajustado, de su preferencia, asumiendo que existen.
- Θ( 1 )
- Θ(
 )
) - Θ( n )
- Θ( n2 )
- Θ( n3 )
Solución
Esta es una aplicación directa de las definiciones anteriores.
- Los límites ajustados serán O( 1 ) y Ω( 1 ). Un límite O no ajustado sería O( n ). Recuerde que O nos indica un límite superior. Como n es de una mayor magnitud que 1, este es un límite no ajustado y también podemos escribirlo como o( n ). Pero para Ω no podemos encontrar un límite no ajustado, ya que no podemos descender bajo 1 para estas funciones. Así que tendremos que quedarnos con el límite ajustado.
- Los límites ajustados tendrán que ser igual que la complejidad Θ, por lo que son
O(
 ) y
Ω(
) y
Ω(  )
respectivamente. Para límites no ajustados podremos tener O( n ), ya que n es mayor que
)
respectivamente. Para límites no ajustados podremos tener O( n ), ya que n es mayor que
 y por lo tanto es un límite superior para
y por lo tanto es un límite superior para
 .
Como sabemos que este es un límite superior no ajustado, también podemos escribirlo como o( n ). Para un límite inferior no ajustado, simplemente podemos usar Ω( 1 ). Como sabemos que este límite no es ajustado, también podemos escribirlo como ω( 1 ).
.
Como sabemos que este es un límite superior no ajustado, también podemos escribirlo como o( n ). Para un límite inferior no ajustado, simplemente podemos usar Ω( 1 ). Como sabemos que este límite no es ajustado, también podemos escribirlo como ω( 1 ).
- Los límites ajustados son O( n ) y Ω( n ). Dos límites no ajustados podrían ser ω( 1 ) y o( n3 ). De hecho, estos son límites bastante pobres, ya que están lejos de las complejidades originales, pero al usar nuestras definiciones siguen siendo válidos.
- Los límites ajustados son O( n2 ) y Ω( n2 ). Para límites no ajustados, podríamos usar nuevamente ω( 1 ) y o( n3 ) como en nuestro ejemplo previo.
- Los límites ajustados son O( n3 ) y Ω( n3 ) respectivamente. Dos límites no ajustados podrían ser
ω(
 n2 ) y
o(
n2 ) y
o(  n3 ).
Si bien estos límites no son ajustados, son mejores que los que dimos anteriormente.
n3 ).
Si bien estos límites no son ajustados, son mejores que los que dimos anteriormente.
La razón por la cual usamos O y Ω en vez de Θ, incluso cuando O y Ω también pueden entregar límites ajustados se debe a que al encontrar un límite podríamos no ser capaces de distinguir si es ajustado, o simplemente porque tal vez no queremos pasar por el proceso de analizarlo tanto.
Si no se recuerda cabalmente de todos los diferentes símbolos y sus usos, no se preocupe mucho en este momento. Siempre podrá retroceder y revisarlos. Los símbolos más importantes son O y Θ.
También advierta que aunque Ω nos entrega un comportamiento de límite inferior para nuestra función (esto es, hemos mejorado nuestro programa para que ejecute menos instrucciones), aún estamos refiriéndonos a un análisis de peor escenario. Esto se debe a que estamos ingresando el peor input a nuestro programa para un n dado, y analizamos su comportamiento bajo este supuesto.
La siguiente tabla indica los símbolos que hemos introducido y su correspondencia con los símbolos matemáticos de comparación más usuales y que usamos con números. La razón por la que aquí no usamos los símbolos usuales y preferimos letras griegas es para resaltar que estamos haciendo una comparación de comportamiento asintótico, y no una simple comparación.
| Operador de comparación asintótica | Operador de comparación numérica |
|---|---|
| Nuestro algoritmo es o( algo ) | Un número es < algo |
| Nuestro algoritmo es O( algo ) | Un número es ≤ algo |
| Nuestro algoritmo es Θ( algo ) | Un número es = algo |
| Nuestro algoritmo es Ω( algo ) | Un número es ≥ algo |
| Nuestro algoritmo es ω( algo ) | Un número es > algo |
Regla General: Si bien todos los símbolos O, o, Ω, ω y Θ suelen ser útiles, O es el que comúnmente se usa más, ya que es más fácil de determinar que Θ y de mayor valor práctico que Ω. .
Logaritmos
Si sabe qué son los logaritmos, tómese la libertad de omitir esta sección. Como la mayoría de las personas no está familiarizada con los logaritmos, o simplemente los ha olvidado porque no los usa con frecuencia, esta sección esboza una introducción a ellos. Este texto también está dirigido a estudiantes jóvenes que aún no han visto logaritmos en la escuela. Los logaritmos son importantes porque aparecen frecuentemente en el análisis de complejidad. Un logaritmo es una operación que al aplicarla en un número, lo hace bastante menor – algo así como la raíz cuadrada de un número. Por esto, si hay algo que querrá recordar acerca de los logaritmos es que procesan un número y lo dejan mucho más pequeño que el original (ver Figura 4).Ahora, en el mismo modo que las raíces cuadradas son la operación inversa de elevar algo al cuadrado, los logaritmos son la operación inversa de exponenciar alguna cosa. Esto no es tan complicado como parece. Queda mejor explicado con un ejemplo.
2x = 1024
Ahora querremos resolver esta ecuación para x. por lo que nos preguntamos: ¿A qué número debemos elevar la base 2 para que obtengamos 1024? Ese número es 10. De hecho, tenemos que 210 = 1024, lo cual es fácil de verificar. Los logaritmos nos ayudan a denotar este problema utilizando una notación nueva. En este caso, 10 es el logaritmo de 1024 y lo escribimos como log( 1024 ) y lo leemos como "el logaritmo de 1024". Debido a que estamos usando 2 como base, estos logaritmos se denominan logaritmos de base 2. Existen logaritmos con otras bases pero en este artículo usaremos logaritmos de base 2 solamente. Si usted es un estudiante que compite en certámenes internacionales y no conoce los logaritmos, le sugiero enfáticamente que los ejercite después de leer este artículo. En las ciencias computacionales, los logaritmos de base 2 son mucho más comunes que otro tipo de logaritmos. Esto se debe a que usualmente tenemos dos entidades distintas: 0 y 1. También tendemos a simplificar un gran problema en mitades, de las cuales siempre hay 2. En consecuencia, sólo necesita manejar los logaritmos de base 2 para continuar con este artículo.
Ejercicio 7
Resuelva las siguientes ecuaciones. Indique en cada caso qué logaritmos está buscando. Use logaritmos en base 2.
- 2x = 64
- (22)x = 64
- 4x = 4
- 2x = 1
- 2x + 2x = 32
- (2x) * (2x) = 64
Solución
Aquí no hay que hacer nada más que aplicar las ideas que ya definimos.
- Por prueba y error encontramos que x=6 y por lo tanto log( 64 )=6
- Aquí advertimos que (22)x,por las propiedades de los exponentes, puede ser escrito como 22x. Luego llegamos a que 2x=6 debido a que log( 64 )=6, obtenido anteriormente, y por tanto x = 3.
- Usando los hallazgos de la ecuación anterior, podemos escribir 4 como 2^2 por lo que nuestra ecuación queda (22)x = 4 lo cual es lo mismo que 22x = 4 Luego notamos que log( 4 )=2, porque 2^2=4. En consecuencia tenemos que 2x=1, por lo que x=1. Esto puede observarse directamente de la ecuación original, ya que el uso de 1 como exponente entrega la base como resultado.
- Recuerde que el 0 como exponente da como resultado 1. Entonces si tenemos log( 1 )=0 como 2^0=1, obtendremos que x=0.
- Aquí tenemos una suma, por lo que no podemos resolver el logaritmo directamente. Sin embargo podemos notar que 2x + 2x es igual que 2 * (2x). Es decir, hemos puesto en la multiplicación otro 2, y por tanto esto es lo mismo que 2x + 1 Ahora nos queda resolver la ecuación 2x + 1 = 32. Encontramos que log( 32 )=5 y que x+1=5 y en consecuencia x=4.
- stamos multiplicando dos potencias de 2, por lo que podemos juntarlas al advertir que (2x) * (2x) es igual que 22x. Luego, solamente tenemos que resolver la ecuación 22x = 64 para la cual ya obtuvimos que x = 3.
Regla General: Para comparar algoritmos implementados en C++, una vez que haya analizado la complejidad, podrá hacer un estimativo aproximado de qué tan rápido corre su programa al esperar que realice cerca de 1000000 operaciones por segundo, en donde las operaciones contadas son dadas por la función de comportamiento asintótico que describe su algoritmo. Por ejemplo, un algoritmo Θ( n ) se tarda cerca de un segundo para procesar el input para n=1000000.
Complejidad Recursiva
Fijémonos ahora en las funciones recursivas. Una función recursiva es una función que hace referencia a sí misma. ¿Podemos analizar su complejidad= La siguiente función, escrita en Python, evalúa el factorial de un número dado. El factorial de un número entero positivo se obtiene al multiplicarlo con todos los enteros positivos previos. Por ejemplo, el factorial de 5 sería 5 * 4 * 3 * 2 * 1. Esto lo denotamos como "5!" y lo pronunciamos como "cinco factorial" (algunas personas prefieren decirlo con un grito escandaloso, algo así como "¡¡¡CINCO!!!")
def factorial( n ):
if n == 1:
return 1
return n * factorial( n - 1 )
Ahora, analicemos la complejidad de esta función. Esta función no contiene bucles en su interior, pero su complejidad tampoco es constante. Para encontrar esta complejidad tenemos que recurrir a instrucciones de conteo. Claramente, si ingresamos un n a esta función, se ejecutará n veces. Si no está seguro de eso, compruebe que realmente funciona ejecutándola "a mano" para un n=5. Por ejemplo, para n=5, se ejecutará 5 veces, a la vez que irá disminuyendo n en 1 con cada corrida. De esta forma, podemos notar que esta función es Θ( n ).
Si tiene dudas en este punto, recuerde que siempre puede encontrar la complejidad exacta mediante instrucciones de conteo. Si lo desea, puede intentar el conteo de la cantidad efectiva de instrucciones realizadas por esta función para hallar una función f( n ) y ver que de hecho es lineal (recuerde que lineal significa Θ(n)).
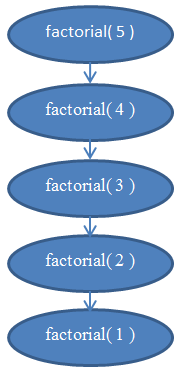
Revise el diagrama de la Figura 5 para entender las recursiones realizadas cuando factorial( 5 ) se ejecuta.
Esto debería aclarar el porqué esta función es de complejidad lineal.
Complejidad Logarítmica
Un famoso problema en ciencias computacionales es el de buscar un valor determinado dentro de un array. Anteriormente ya resolvimos en un caso general. Este problema se torna interesante si tenemos un array que está ordenado y queremos un valor dado dentro de él. Una forma de hacer esto es mediante la denominada "binary search" o "búsqueda binaria". Nos fijamos en el elemento central de nuestro array: Si lo hallamos ahí, hemos finalizado. De otro modo, si el valor que encontramos allí es mayor que el valor que buscamos, sabemos que nuestro elemento estará en el lado izquierdo del array. Si no, sabremos que estará en el lado derecho. Podemos seguir dividiendo estos pequeños arrays en pequeñas mitades más pequeñas hasta que tengamos sólo un elemento que analizar. Usando un pseudo código, el método queda de esta forma:
def binarySearch( A, n, value ):
if n = 1:
if A[ 0 ] = value:
return true
else:
return false
if value < A[ n / 2 ]:
return binarySearch( A[ 0...( n / 2 - 1 ) ], n / 2 - 1, value )
else if value > A[ n / 2 ]:
return binarySearch( A[ ( n / 2 + 1 )...n ], n / 2 - 1, value )
else:
return true
Teste pseudo código es una simplificación de una implementación real. En la práctica, este método es más fácil de describir que implementar, ya que los programadores necesitan fijarse en algunos detalles al aplicarlo. Existen errores "off-by-one", y también puede ser que la división por dos no siempre entregue un valor entero, por lo que podría ser necesario aplicar floor() o ceil() al valor. Pero, para nuestros propósitos, podremos asumir que siempre tendremos éxito, y consideraremos que la aplicación concreta se ocupará de los errores "off-by-one", ya que solamente nos interesa analizar la complejidad de este método. Si usted nunca ha puesto en marcha una búsqueda binaria, le recomiendo hacerlo en su lenguaje de programación favorito. Es un esfuerzo que le será muy provechoso.
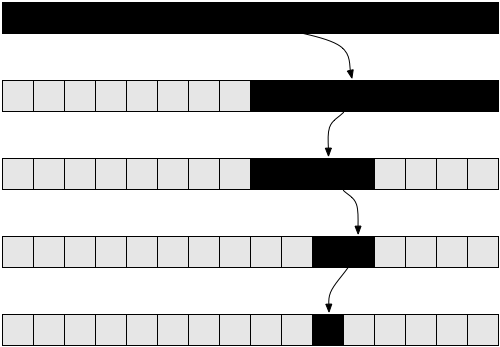
Revise la Figura 6 para entender cómo opera la búsqueda binaria.
Si no está seguro de cómo funciona concretamente este método, dese un tiempo para ejecutarlo a mano en este sencillo ejemplo y convénzase de que realmente funciona.
Ahora intentemos analizar este algoritmo. En este caso tenemos nuevamente un algoritmo recursivo. Demos por sentado, por simplicidad, que el array siempre puede dividirse exactamente en dos, ignorando por ahora la parte +1 y el -1 en la invocación recursiva. Por ahora, debería estar convencido de que un pequeño cambio, como ignorar el +1 y el -1 no alterará nuestros resultados de complejidad. Esto es un hecho que normalmente tendríamos que probar si quisiéramos ser matemáticamente correctos, pero en la práctica es algo intuitivamente obvio. Para simplificar, asumamos que nuestro array tiene un tamaño que es una potencia exacta de 2. Nuevamente, esta conjetura no altera el resultado final de complejidad, al que llegaremos posteriormente. El peor escenario para este problema podría ocurrir cuando el valor que buscamos no aparece en nuestro array en absoluto. En este caso, comenzaremos con un array de tamaño n, en el primer llamado a la recursión, de modo de obtener un array de tamaño n/2 en el siguiente llamado. Luego, en el siguiente llamado recursivo obtendremos un array de tamaño n/4, seguido por un array de tamaño n/8, y así consecutivamente. En general, nuestro array se divide por la mitad en cada llamado, hasta que llegamos a 1. Entonces, escribamos la cantidad de elementos en nuestro array en cada llamado:
Note que en cada i-ésima iteración, nuestro array tiene n / 2i elementos. Esto se debe a que en cada iteración cortamos el array en dos, lo que significa que también dividimos su cantidad de elementos en dos. Esto se traduce en multiplicar el denominador con un 2. Si hacemos esto i veces, obtendremos n / 2i.Luego, este procedimiento continua, y con cada i mayor, obtenemos un menor número de elementos hasta que alcancemos la última iteración en la cual sólo nos queda 1 elemento. Si queremos encontrar el i correspondiente a la iteración en que esto ocurrirá, tenemos que resolver la siguiente ecuación:
1 = n / 2i
Esto será verdad solamente cuando hayamos llegado a la última invocación de la función binarySearch() o de búsqueda binaria, y no en el caso general. Entonces, si despejamos para i, podremos saber en qué iteración la recursión finalizará. Multiplicando ambos lados por 2i obtenemos:
2i = n
Ahora, esta ecuación debería ser familiar si es que lee la sección previa de logaritmos. Resolviendo para i, obtenemos:
i = log( n )
Esto nos indica que el número requerido de iteraciones para realizar una búsqueda binaria es log( n ), en donde n es el número de elementos de nuestro array original.
Si lo piensa, esto tiene sentido. Por ejemplo, tome n=32, un array de 32 elementos. ¿Cuántas veces tenemos que dividir esto en mitades para llegar a sólo 1 elemento? Tenemos 32 → 16 → 8 → 4 → 2 → 1. Hicimos esto 5 veces, lo cual es el logaritmo de 32. Por lo tanto, la complejidad de la búsqueda binaria es Θ( log( n ) ). .
Este último resultado nos permite comparar la búsqueda binaria con la búsqueda lineal, nuestro método anterior. Claramente, como log( n ) es mucho menor que n, es razonable concluir que la búsqueda binaria es un método mucho más rápido que la búsqueda lineal para buscar dentro de un array. Por esto, es aconsejable que mantengamos nuestros arrays ordenados si queremos buscar muchas veces en ellos.
Regla General: Mejorar el tiempo de ejecución asintótica de un programa generalmente mejora ostensiblemente su desempeño, mucho más que pequeñas optimizaciones técnicas, tales como usar un lenguaje de programación más rápido.
Ordenamiento Óptimo
Felicitaciones. Ahora ya sabe cómo analizar la complejidad de los algoritmos, entender el comportamiento asintótico de las funciones y utilizar la notación Big-O. También sabe como llegar intuitivamente a que la complejidad de un algoritmo es O( 1 ), O( log( n ) ), O( n ), O( n2 ), y así sucesivamente. Conoce los símbolos o, O, ω, Ω y Θ y qué significa el análisis de peor escenario. Si ha llegado hasta este punto, este tutorial ya ha cumplido con su objetivo.
Esta sección final es opcional. Es un poco más complicada, por lo que si se siente abrumado, tómese la libertad de omitirla. Requerirá que destine tiempo en trabajar con los ejercicios. Sin embargo, le entregará un método muy útil para el análisis de complejidad de algoritmos, el cual vale la pena comprender debido al gran potencial que tiene.
Anteriormente vimos la implementación de una forma de ordenamiento, llamada ordenamiento por selección. Mencionamos que el ordenamiento por selección no es óptimo. Un algoritmo óptimo es un algoritmo que resuelve un problema de la mejor forma posible, lo que significa que no existen mejores algoritmos para esto. Lo anterior indica que todos los otros algoritmos para resolver este problema tienen una complejidad peor o igual que el algoritmo óptimo. Puede darse que existan muchos algoritmos óptimos para un problema y que todos compartan la misma complejidad. El problema de ordenamiento puede ser resuelto óptimamente de diversas formas. Podemos aplicar la misma idea con la búsqueda binaria, para ordenar rápidamente. Éste método de ordenamiento se denomina "merge sort" u "ordenamiento por mezcla".
Para realizar un ordenamiento por mezcla, primero tenemos que construir una función auxiliar que posteriormente usaremos para concretamente realizar la búsqueda. Haremos una función de
merge la cual tomará dos arrays que ya están ordenados, y los unirá en un gran array ordenado. Esto se logra fácilmente:
def merge( A, B ):
if empty( A ):
return B
if empty( B ):
return A
if A[ 0 ] < B[ 0 ]:
return concat( A[ 0 ], merge( A[ 1...A_n ], B ) )
else:
return concat( B[ 0 ], merge( A, B[ 1...B_n ] ) )
La función concat toma un ítem, la "cabeza", y un array, la "cola", construye y entrega un nuevo array que contiene la ítem "cabeza" como lo primero en el nuevo array y el iten "cola" como el resto de los elementos en el array. Por ejemplo, concat( 3, [ 4, 5, 6 ] ) entrega [ 3, 4, 5, 6 ]. Utilizamos A_n y B_n para denotar los tamaños de los arrays A y B respectivamente.
Ejercicio 8
Verifique que las funciones anteriores realmente ejecutan una mezcla. Reescríbalo en su lenguaje de programación favorito en una forma iterativa (utilizando bucles l) en lugar de usar recursión.
El análisis de este algoritmo demuestra que tiene un tiempo de ejecución Θ( n ), en donde n es la longitud del array resultante (n= A_n + B_n).
Ejercicio 9
Compruebe que el tiempo de ejecución de la mezcla es Θ( n ).
Utilizando esta función podremos construir un mejor algoritmo de or denamiento. La idea es la siguiente: dividimos el array en dos partes. Orde namos cada una de las partes recursivamente y luego unimos los dos arreglos ya ordenados en un array mayor. En pseudocódigo:
def mergeSort( A, n ):
if n = 1:
return A # it is already sorted
middle = floor( n / 2 )
leftHalf = A[ 1...middle ]
rightHalf = A[ ( middle + 1 )...n ]
return merge( mergeSort( leftHalf, middle ), mergeSort( rightHalf, n - middle ) )
En relación a lo que ya hemos visto, esta función es más intrincada de entender, por lo que el siguiente ejercicio le puede tomar algunos minutos.
Ejercicio 10
Verifique si mergeSort. está correcto. Esto es, revise si mergeSort
definido de la manera anterior, realmente ordena de forma correcta el array que se le entrega. Si tiene dificultades para comprender por qué funciona, trate con un array de ejemplo más pequeño y córralo "a mano". Cuando ejecute esta función a mano, asegúrese que la parte izquierda y la parte derecha son lo que obtendría si cortara el array aproximadamente en la mitad; no tiene que ser exactamente en la mitad si el array tiene un número impar de elementos (para eso usamos la función
floor anteriormente).
Como ejemplo final, analicemos la complejidad de mergeSort. En cada paso de mergeSort,
estamos dividiendo el array en dos mitades de igual tamaño, de forma similar a binarySearch.
Sin embargo, en este caso, mantenemos ambas mitades durante la ejecución. Luego aplicamos recursivamente el algoritmo en cada una de las mitades. Luego de que la recursión vuelve, aplicamos la operación de
mezcla en el resultado, la cual se demora Θ( n ).
Entonces, dividimos el array original en dos arrays de tamaño n / 2 cada uno. Luego mezclamos esos arrays, una operación que mezcla n elementos, demorándose Θ( n ) tiempo.
De una mirada a la Figura 7 para entender esta recursión.
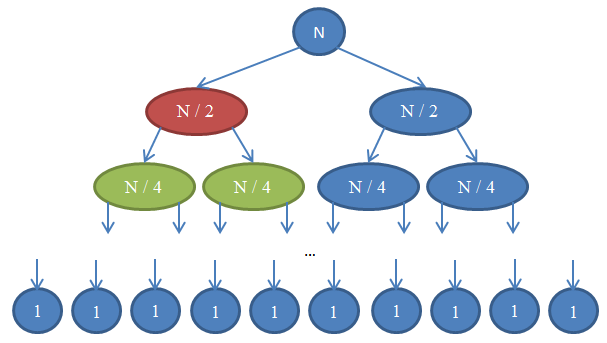
Veamos qué es lo que se nos muestra. Cada círculo representa un llamado a la función mergeSort
El número escrito en el círculo indica el tamaño del array que está siendo ordenado. El círculo superior azul es el llamado original a
mergeSort,en donde ordenamos un array de tamaño n.
La flecha indica llamados recursivos hechos entre las funciones. El llamado original hecho a
mergeSorten dos arrays de tamaño n/2, dos llamados a mergeSort.
Esto está indicado por las flechas en la parte superior. A su vez, cada uno de estos llamados hace dos llamados por su cuenta para que
mergeSort ordene dos arrays de tamaño n/4 cada uno, y así sucesivamente hasta que llegamos a arrays de tamaño 1. Este diagrama se llama "árbol de recursiones", porque ilustra como las recursiones se comportan, asimilándose a un árbol (la raíz está en lo alto y las hojas abajo, así que en realidad parece un árbol invertido).
En el diagrama anterior, note que en cada fila el número total de elementos es n. Para verificar esto, fíjese en cada fila individualmente. La primera fila contiene sólo un llamado a
mergeSort entro del array de tamaño n, or lo que el número total de elementos es n.
La segunda fila tiene dos llamados a mergeSort
cada uno de tamaño n / 2. Pero n / 2 + n / 2 = n y, nuevamente, el número total de elementos en esta fila es
n. En la tercera fila, tenemos 4 llamados, cada uno de los cuales es aplicado en un array de tamaño n / 4, generando un número total de elementos igual a n / 4 + n / 4 + n / 4 + n / 4 = 4n / 4 = n. Por lo que nuevamente tenemos
nelementos. Ahora, note que en cada fila de este diagrama el llamador tendrá que realizar una operación de
merge en los elementos devueltos por los receptores de las llamadas. Por ejemplo, el círculo indicado con color rojo tiene que ordenar n/2 elementos. Para hacer esto, separa el array de tamaño n/2 en dos arrays de tamaño n/4, llama a
mergeSort recursivamente para que los ordene (estas llamadas son los círculos indicados en color verde), y luego los mezcla. Esta operación implica la mezcla de n/2 elementos. En cada fila de nuestro árbol, el número total de elementos mezclados es n. En la fila que hemos estado explorando, nuestra función mezcla n/2 elementos y la función a su derecha (aquella de color azul) también tiene que mezclar n/2 elementos por sí misma. Eso genera n elementos en total, los cuales tienen que ser mezclados en la fila que estamos mirando.
Debido a lo anterior, la complejidad de cada fila es Θ( n ). Sabemos que el número total de filas en este diagrama, también denominado la "profundidad del árbol de recursividad", será log( n ). El razonamiento detrás de esto es exactamente el mismo que utilizamos cuando hicimos el análisis de complejidad de una búsqueda binaria. Tenemos log( n ) filas y cada una de ellas es Θ( n ), por lo que la complejidad del ordenamiento por mergeSort es Θ( n * log( n ) ).Esto es mucho mejor que Θ( n2 ) lo cual es lo que el ordenamiento por selección nos dio (recuerde que log(n) es mucho menor que n, por lo que n * log( n ) es mucho menor que n * n = n2). Si esto le parece complicado, no se preocupe: no es algo sencillo la primera vez que se ve. Vuelva a esta sección y relea las discusiones que hemos hecho, luego de haber implementado el ordenamiento por mezcla en su lenguaje de programación favorito y compruebe que funciona.
Como vio el último ejemplo, el análisis de complejidad nos permite comparar algoritmos para verificar cuál es mejor. Bajo estas circunstancias, podemos tener la certeza de que el ordenamiento por mezcla superará la ordenamiento por selección en arrays grandes. Esta conclusión podría ser difícil de visualizar si es que no tuviésemos la base teórica de análisis de algoritmos que hemos desarrollado. En la práctica, se usan algoritmos de ordenamiento con tiempo de ejecución del tipo Θ( n * log( n ) ). Por ejemplo, el kernel de Linux utiliza un algoritmo de ordenamiento llamado "heapsort", el cual tiene el mismo tiempo de ejecución que el ordenamiento por mezcla, a saber Θ( n * log( n ) ), y por tanto es óptimo. Note que no hemos probado que estos algoritmos de ordenamiento son óptimos. Hacer esto requiere un desarrollo matemático más avanzado, pero tenga la certeza de que no es posible mejorar aún más desde un punto de vista de complejidad.
Ahora que ha terminado con la lectura de este tutorial, la intuición que ha desarrollado para el análisis de complejidad de algoritmos le permitirá diseñar programas más rápidos y también lo ayudará a trabajar de forma más productiva, orientando sus esfuerzos de optimización hacia aquello que realmente es importante, dejando de lado detalles superficiales. Adicionalmente, el lenguaje matemático y la notación que hemos desenvuelto, tal como la notación Big-O, es de gran utilidad para comunicarse con otros ingenieros de software a la hora de discutir acerca de tiempos de ejecución de algoritmos, lo cual, espero que pueda ponerlo en práctica con los nuevos conocimientos que ha adquirido.
Acerca del Artículo
Este artículo tiene licencia Creative Commons 3.0 Attribution. Esto significa que puede copiarlo/pegarlo, compartirlo, publicarlo en su website, modificarlo y, en general, hacer lo que quiera con él, siempre y cuando mencione mi nombre. Aunque no es necesario que lo haga, si basa su trabajo en el mío, lo animo a que también publique sus escrito bajo licencia Creative Commons, de modo de que sea más fácil para todos compartirlo y colaborar en conjunto. De igual forma, yo debo referirme a los trabajos que he ocupado. Los estilosos íconos que usted ve en esta página son iconos fugue.. El bello patrón a rayas que puede apreciar en el diseño, fue creado por Lea Verou. Y, lo más importante, los algoritmos que domino, y que por tanto, pude escribir aquí, fueron enseñanzas que recibí de mi profesor Dimitris Fotakis.
En este momento soy un estudiante de Ingeniería Eléctrica y Computacional en la Universidad Técnica Nacional de Atenas especializándome e software y desempeñándome como entrenador en la Competición Griega en Informática. En contextos empresariales, he trabajado en el equipo de ingeniería que desarrolló deviantART, una red social para artistas, y en dos puestas en marcha, Zino y Kamibu, en donde hicimos el desarrollo redes sociales y de videojuegos, respectivamente. Si le gustó este artículo y quiere mantenerse en contacto, sígame en Twitter o en github o si prefiere, escríbame por correo electrónico. Muchos programadores jóvenes no tienen una buena base en el idioma Inglés. Escríbame si desea traducir este artículo a su lenguaje nativo, para que sea asequible a más personas.
Gracias por leer No recibí dinero por escribir este artículo, por lo que si le gustó, envíeme un e-mail con saludos. Me agrada mucho recibir fotos de distintos lugares del mundo, por lo que no dude en adjuntar una foto suya en su ciudad!
Referencias
- Cormen, Leiserson, Rivest, Stein. Introduction to Algorithms, MIT Press.
- Dasgupta, Papadimitriou, Vazirani. Algorithms, McGraw-Hill Press.
- Fotakis. Course of Discrete Mathematics at the National Technical University of Athens.
- Fotakis. Course of Algorithms and Complexity at the National Technical University of Athens.

