Доступне введення в аналіз складності алгоритмів.
Dionysis "dionyziz" Zindros <dionyziz@gmail.com>Переклад: Y. E. T.
- English
- Ελληνικά
- македонски
- Español
- Nederlands
- עברית
- Português
- srpskohrvatski
- Українська
- Русский
- Help translate
Вступ
Багато хто з сучасних програмістів — тих що створюють круті та надзвичайно корисні програми, які ми бачимо в Інтернеті або використовуємо щодня — не мають теоретичних знань з інформатики. Все одне такі програмісти є відмінними фахівцями, і ми вдячні їм за те, що вони роблять.
Однак теоретичні знання мають прикладне значення і можуть бути використані для розв'язання практичних проблем. Ця стаття призначена для програмістів, які знають своє мистецтво, але не мають теоретичних знань. Я познайомлю вас з одним із прагматичних інструментів інформатики: аналіз складності алгоритмів. Я працював як в академічних колах, так і в області прикладної розробки програмного забезпечення, і виявив, що це дійсно корисний інструмент. Тому я сподіваюся, що прочитавши цю статтю, і ви зможете застосувати його для поліпшення коду. Ви зрозумієте загальноприйняті терміни в інформатиці, такі як «О» велике, асимптотична поведінка й аналіз найгіршого випадку.
Цей текст також призначений для учнів середніх і старших класів, які беруть участь у Міжнародній олімпіаді з інформатики або інших подібних конкурсах. Таким чином, ця стаття не вимагає від вас глибоких математичних знань і надає необхідний теоретичний матеріал для подальшого вивчення алгоритмів. Я сам брав участь у таких конкурсах, а тому наполегливо рекомендую уважно прочитати весь вступний матеріал і спробувати повністю його зрозуміти, оскільки це необхідно для подальшого вивчення алгоритмів і більш складних методів їх аналізу.
Цей текст буде корисним для програмістів практиків, яким не вистачає теоретичних знань (деякі з найбільш надихаючих інженерів програмного забезпечення не мають вищої освіти). Однак майте на увазі, що стаття також написана для учнів, тому час від часу вона може нагадувати підручник. Деякі теми можуть бути занадто простими для вас; наприклад, якщо ви вже зустрічалися з ними. В такому випадку можете перейти до наступної теми. Наступні розділи більше заглиблюються в розглянуті питання і набувають теоретичне забарвлення, оскільки студенти, які беруть участь у змаганнях, потребують цих знань. Однак усі теми, які тут обговорюються, корисно знати; вони доступні для розуміння й тому, швидше за все, гідні вашого часу.
У цій статті ви знайдете посилання на цікавий матеріал, що виходить за рамки даної теми. Якщо ви професійний програміст, швидше за все ви вже знайомі з більшою частиною такого матеріалу. Якщо ви учень, який бере участь у змаганнях, вивчення додаткового матеріалу допоможе вам познайомитися з іншими областями інформатики та програмування і, можливо, розширити коло ваших інтересів.
Велика кількість програмістів та учнів вважає, що аналіз складності алгоритмів важкий для розуміння. Вони бояться його або навіть повністю його уникають. Насправді «O» велике й аналіз складності алгоритмів не такі важкі для розуміння, як це може здаватися. Аналіз складності алгоритмів — це всього лише спосіб оцінити швидкість роботи програми або алгоритму, так що це дуже практичний інструмент. Почнімо з невеликої мотивації.

Мотивація
Ми вже знаємо про існування інструментів, що вимірюють швидкість роботи коду. Ці програми називаються профайлерами (англ. profilers). Профайлери вимірюють тривалість роботи коду в мілісекундах і допомагають виявляти вузькі місця (англ. bottleneck) в роботі коду, для подальшої його оптимізації. При всій корисності таких інструментів, профайлери не мають відношення до складності алгоритмів. Аналіз складності алгоритмів був розроблений для порівняння алгоритмів на рівні їхніх ідей, ігноруючи несуттєві деталі: використані мова програмування, обладнання, набір команд центрального процесора. Ми хочемо порівняти сутність алгоритмів: ідеї, яким чином має бути здійснене обчислення. Підрахунок мілісекунд не допоможе нам впоратися з таким завданням. Цілком ймовірно, що поганий алгоритм, написаний мовою низького рівня — наприклад мовою асемблера — відпрацює набагато швидше хорошого алгоритму, написаного високорівневою мовою програмування — наприклад мовою Python або Ruby. Отже, настав час дати визначення поняттю «кращий алгоритм».
Оскільки алгоритми — це програми, зайняті обчисленнями (на відміну від інших завдань, які виконуються комп'ютерами: мережевих, введення та виведення даних користувачем), аналіз складності дозволяє нам виміряти швидкість роботи програми. Приклади суто обчислювальних операцій охоплюють операції з числами, представленими у формі з рухомою комою (такі як додавання й множення); пошук по базі даних в оперативній пам'яті (англ. in-memory database); знаходження найкоротшого шляху для персонажа, керованого штучним інтелектом (Ілюстрація 1); або ж пошук у тексті з використанням регулярних виразів. Очевидно, що обчислювальні завдання зустрічаються повсюдно в комп'ютерних програмах.
Аналіз складності також дозволяє описати, як алгоритм поводиться при збільшенні розміру вхідних даних. Як поведе себе алгоритм отримавши іншу кількість вхідних даних? Якщо наш алгоритм відпрацьовує за 1 секунду, отримавши 1000 одиниць вхідних даних, то як він поведе себе, отримавши в два рази більше даних? Чи буде він працювати з тією ж швидкістю або в два рази повільніше, або в чотири рази повільніше? Аналіз складності дозволяє передбачати поведінку алгоритму, що важливо для прикладного програмування. Припустимо, ми написали алгоритм для вебдодатку так, що він гарно працює з даними 1000 користувачів, і виміряли наскільки швидко він справляється зі своїм завданням. Тоді аналіз складності алгоритму дозволяє нам оцінити швидкість алгоритму при роботі з даними 2000 користувачів. Для змагань з інформатики, аналіз складності дає розуміння, скільки часу знадобиться нашому коду, щоб обробити найбільші тестові дані, які використовуються для перевірки правильності роботи нашої програми. Таким чином, якщо ми виміряємо швидкість роботи програми з малою кількістю вхідних даних, тоді ми можемо оцінити, яка буде швидкість її роботи з великою кількістю даних. Почнемо з простого прикладу: знаходження найбільшого елементу в масиві даних.
Підрахунок інструкцій
У цій статті приклади коду будуть написані на різних мовах програмування. Не засмучуйтесь, якщо ви не знайомі з будь-якими з них. Усі приклади будуть простими, без використання езотеричних можливостей мов, так що людина, знайома з програмуванням, зможе зрозуміти всі приклади без проблем. Якщо ви учень, який бере участь у змаганнях, ви найімовірніше знайомі з C ++, так що приклади й для вас повинні бути зрозумілими. Учням я рекомендую попрактикуватися з прикладами, написавши їх на C ++.
Ми можемо знайти найбільший елемент масиву використовуючи показаний нижче фрагмент Javascript коду. Припустимо нам дано масив даних A з розміром n >= 1. Тоді:
var M = A[ 0 ];
for ( var i = 0; i < n; ++i ) {
if ( A[ i ] >= M ) {
M = A[ i ];
}
}
Спочатку ми підрахуємо кількість базових команд у цьому фрагменті коду. Ми зробимо такий підрахунок тільки один раз. Необхідність у ньому пропаде у міру розбору теорії, так що наберіться трохи терпіння. Під час аналізу цього фрагменту коду, ми хочемо розбити його на прості команди: ті, які можуть бути виконані процесором безпосередньо (або близько до цього). Припустимо, що наш процесор може виконувати такі операції як одну команду:
- Присвоїти значення змінної.
- Знайти значення заданого елемента в масиві.
- Порівняти два значення.
- Збільшити значення на одиницю (інкремент).
- Провести базові арифметичні дії (додавання, віднімання).
Ми припустимо, що розгалуження (вибір між частинами коду в тілі if або else) відбувається миттєво, і не будемо підраховувати ці команди. Розглянемо перший рядок коду, показаного вище:
var M = A[ 0 ];
Цей рядок містить дві команди: одна знаходить елемент масиву A[ 0 ], інша привласнює знайдену величину змінній M. Алгоритм завжди виконує ці дві команди, незалежно від значення n. Цикл for теж виконується завжди та дає нам ще дві команди: присвоювання і порівняння.
i = 0;
i < n;
Вони відпрацюють до першої ітерації циклу for. Після кожної ітерації циклу for, відпрацюють ще дві команди: інкременту та порівняння (для перевірки, чи залишаємося ми в циклі):
++i;
i < n;
Ми ігноруємо тіло циклу, тому кількість команд, що виконуються цим алгоритмом, дорівнює 4 + 2n. А саме, 4 команди на початку циклу for і 2 команди в завершенні кожної ітерації (всього здійснюється n ітерацій). Тепер ми можемо визначити математичну функцію f( n ), яка співвідносить n з кількістю команд, які виконуються алгоритмом. При порожньому тілі циклу for, f( n ) = 4 + 2n.
Аналіз найгіршого випадку
Наразі подивимося на тіло циклу for. Тут завжди здійснюються пошук у масиві й операція порівняння:
if ( A[ i ] >= M ) { ...
Тобто в тілі циклу виконуються дві команди. Однак виконання або невиконання команд у тілі if залежить від значень елементів масиву. Якщо A[ i ] >= M, тоді відпрацюють ще дві команди: пошуку в масиві та присвоювання:
M = A[ i ]
Але тепер ми більше не можемо легко визначити f( n ), тому що кількість команд залежить не тільки від n, але й від значень, що вводяться. Наприклад, при A = [ 1, 2, 3, 4 ], алгоритму знадобиться виконати більше команд, ніж при A = [ 4, 3, 2, 1 ]. При аналізі алгоритмів часто розглядається найгірший сценарій. Які вхідні дані самі несприятливі для нашого алгоритму? В якому випадку алгоритму знадобиться виконати максимальну кількість операцій? Для розглянутого прикладу найгірший варіант — це отримати масив, відсортований за зростанням, наприклад: A = [ 1, 2, 3, 4 ]. У такому випадку з кожною новою ітерацією значення i-го елементу масиву буде присвоєно M, а це є максимальна кількість команд. Для таких випадків у теоретиків є чудна назва: аналіз найгіршого випадку; але це всього лише розгляд самого невдалого варіанту. Отже, у найгіршому разі в тілі циклу for відпрацює 4 команди. Разом, f( n ) = 4 + 2n + 4n = 6n + 4. Функція f при заданій проблемі з розміром n дає нам кількість команд, виконуваних у найгіршому випадку.
Асимптотична поведінка
Отримана вище функція дає нам досить чітке уявлення про швидкість роботи алгоритму. Однак, як я й обіцяв, нам не знадобиться кожного разу займатися трудомістким підрахунком кількості команд у програмі. До того ж кількість реальних команд, які виконуються процесором, залежить від компілятора нашої мови програмування та від типу самого процесора. Як ми вже говорили, ми ігноруємо цю різницю. Зараз ми пропустимо нашу функцію «f» крізь «фільтр», який допоможе нам позбутися несуттєвих деталей, ігнорованих під час аналізу.
Функція f( n ) = 6n + 4 складається з двох членів: 6n і 4. При аналізі складності нас цікавить, що відбувається з функцією підрахунку команд при збільшенні кількості вхідних даних n. Цей підхід добре відповідає аналізу поведінки у найгіршому випадку: нам цікаво дізнатися, як алгоритм поведе себе в «поганих» умовах (при необхідності обробити важку задачу). Зауважте, що це дуже зручно для порівняння алгоритмів між собою. Якщо один алгоритм «перемагає» в іншого при великій кількості вхідних даних, тоді найбільш імовірно, що швидкіший алгоритм залишиться таким і при меншій кількості вхідних даних. Тому, ми знехтуємо членами функції, які ростуть повільно, і залишимо ті, які ростуть дуже швидко при збільшенні n. Явно, що 4 залишиться рівним 4 при будь-якому значенні n. При цьому 6n постійно зростатиме зі збільшенням значення n, так що саме 6n гратиме все більшого значення зі збільшенням вхідних даних. Отже, ми можемо знехтувати значенням 4 і записати нашу функцію в такому вигляді: f( n ) = 6n.
І це розумний підхід, адже 4 — всього лише «константа ініціалізації». Різні мови програмування потребують різну кількість часу для ініціалізації. Наприклад, мові Java потрібна значна кількість часу для запуску віртуальної машини. Через то, що ми ігноруємо відмінності між мовами програмування, буде правильно знехтувати й константою 4.
Ще один елемент, яким можна знехтувати — це постійний множник 6. Таким чином, нашу функцію можна записати в такому вигляді: f( n) = n. Як бачите, ми дуже сильно спростили процедуру підрахунку команд. І це знову виглядає як розумний підхід, беручи до уваги, що різні мови програмування компілюються по-різному. Наприклад мова C, виконуючи інструкцію A[ i ], не перевіряє, чи знаходиться значення «i» в діапазоні розміру масиву. Разом з тим Паскаль робить таку перевірку. Іншими словами, наступний фрагмент коду на мові Паскаль:
M := A[ i ]
є еквівалентним такому фрагменту на мові C:
if ( i >= 0 && i < n ) {
M = A[ i ];
}
Так що під час підрахунку команд прийнятно очікувати різні множники у випадку різних мов програмування. В нашому прикладі для мови Паскаль використовується найпримітивніший компілятор, без будь-якої оптимізації. У такому випадку Паскаль потребує 3 команди для кожного запиту до масиву даних; замість лише 1 команди, що виконується мовою C. Опускаючи відповідний множник, ми чинимо згідно до вже прийнятого нами підходу ігнорування різниці між мовами програмування й аналізу самої сутності алгоритмів.
Описаний вище фільтр «знехтування множниками та константами» має назву: асимптотична поведінка. Так, асимптотична поведінка функції f( n ) = 2n + 8 описується функцією f( n ) = n. Говорячи математичною мовою, нам цікава межа функції f при n, що прагне до нескінченності. (Якщо вам не зрозумілий сенс цієї фрази, не хвилюйтеся: досить, що ви ознайомилися з цим формулюванням. Примітка: при строгому математичному підході ми не змогли б знехтувати константами; але для задач у сфері інформатики ми це робимо з причин, описаних вище). А тепер опрацюємо пару прикладів, щоб звикнути до вже описаних концепцій.
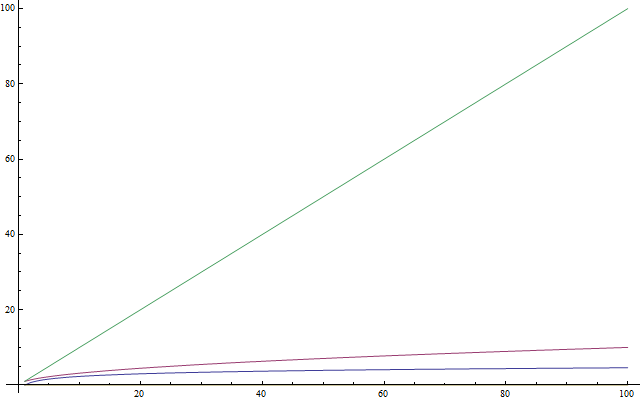
Знайдемо асимптотичну поведінку наступних функцій:
f( n ) = 5n + 12 дає f( n ) = n.
Згідно до вже викладеного ходу думки.
f( n ) = 109 дає f( n ) = 1.
Ми нехтуємо множником 109 * 1, але повинні залишити 1 для позначення, що функція має не нульове значення.
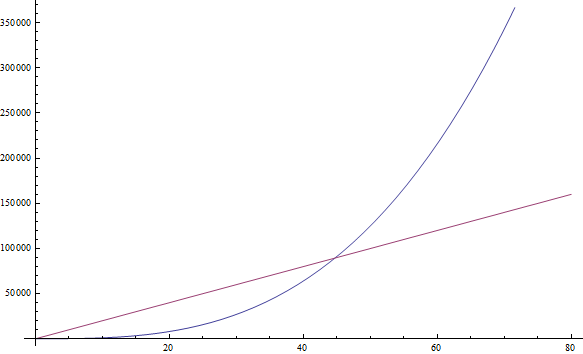
f( n ) = n2 + 3n + 112 дає f( n ) = n2
n2 зростає швидше, ніж 3n, при достатньо великому значенні n.
f( n ) = n3 + 1999n + 1337 дає f( n ) = n3
Множник 1999 досить великий, але ми все ж можемо знайти досить велике значення n, таке, що n3 буде більше, ніж 1999n. А оскільки ми зацікавлені в поведінці при дуже великих значеннях n, то ми залишаємо тільки n3 (дивіться Ілюстрацію 2).
f( n ) = n +
 дає f( n ) = n
дає f( n ) = nЧерез те, що n зростає швидше, ніж
 у міру збільшення n.
у міру збільшення n.
Спробуйте знайти асимптотичну поведінку наступних функцій самостійно:
Вправа 1
- f( n ) = n6 + 3n
- f( n ) = 2n + 12
- f( n ) = 3n + 2n
- f( n ) = nn + n
(Запишіть ваші результати; відповіді дані нижче.)
Якщо у вас виникли проблеми з будь-якої з функцій, підставте в цю функцію велике значення n і порівняйте, який з членів стає більшим. Досить-таки просто, еге ж?
Складність
Отже, через те що ми можемо знехтувати всіма декоративними константами, досить легко визначити асимптотичну поведінку функції підрахунку команд. Дійсно, асимптотичною поведінкою будь-якої програми без циклів буде f (n) = 1, бо кількість команд, які виконуються такою програмою, завжди дорівнюється якійсь константі (це не стосується випадку рекурсії, розглянутого нижче). Асимптотична поведінка будь-якої програми з одним циклом, що проходить від 1 до n, буде f( n ) = n, бо така програма буде викликати якусь постійну кількість команд до початку циклу, після завершення циклу та всередині циклу (команди всередині циклу завжди будуть викликатися n разів).
Такий підхід мусить бути значно легшим, ніж трудомісткий підрахунок усіх команд програми. Через це розглянемо декілька прикладів, щоб звикнути до нього. Наступна програма, написана на мові PHP, перевіряє, чи знаходиться дане значення у масиві A з розміром n:
<?php
$exists = false;
for ( $i = 0; $i < n; ++$i ) {
if ( $A[ $i ] == $value ) {
$exists = true;
break;
}
}
?>
Такий метод пошуку значення в масиві даних називається лінійним пошуком. Це влучне ім'я, бо асимптотичну поведінку цієї програми описує функція f( n ) = n (ми дамо точне визначення «лінійності» в наступному розділі). Зверніть увагу на інструкцію «break», яка може викликати раніше завершення роботи програми (можливо, відразу ж на першому кроці циклу). Згадайте, що нас цікавить тільки найгірший сценарій. Для даної програми — це відсутність шуканого елемента в масиві A. Так що ми все ще маємо f( n ) = n.
Вправа 2
Використовуючи дану вище програму на мові PHP, підрахуйте кількість команд, що викликаються цією програмою в найгіршому випадку, і виведіть функцію підрахунку команд f (n), як ми це вже робили на прикладі Javascript програми. Потім перевірте, що асимптотично ми отримуємо складність f( n ) = n.
Погляньте на програму написану на мові Python. Ця програма складає значення двох елементів масиву та привласнює результат складання новій змінній:
v = a[ 0 ] + a[ 1 ]
Ця програма містить постійну кількість команд, тож f( n ) = 1.
Наступна програма на мові C ++ перевіряє, чи містить вектор (чуднуватий масив) A з розміром n два однакових значення:
bool duplicate = false;
for ( int i = 0; i < n; ++i ) {
for ( int j = 0; j < n; ++j ) {
if ( i != j && A[ i ] == A[ j ] ) {
duplicate = true;
break;
}
}
if ( duplicate ) {
break;
}
}
Ця програма містить в собі вкладені цикли. В такому випадку асимптотична поведінка описується функцією f( n ) = n2.
Підказка: Прості програми можуть бути проаналізовані шляхом підрахунку циклів. Одиничний цикл із n кроками призводить до складності f (n) = n. Додатковий вкладений цикл призводить до складності f( n ) = n2. Цикл всередині циклу всередині циклу дає складність f( n ) = n3.
Якщо програма викликає функцію в тілі циклу, та якщо нам відома кількість команд, виконуваних цією функцією, тоді нескладно підрахувати кількість команд, які виконуються всією програмою. Дійсно, погляньте на такий приклад на мові C:
int i;
for ( i = 0; i < n; ++i ) {
f( n );
}
Якщо нам відомо, що f( n ) виконує n команд, то нам відомо, що кількість команд, які виконуються всією програмою, асимптотично дорівнює n2, бо функція f( n ) буде викликана точно n разів.
Підказка: Якщо нам дана послідовність циклів for, то найповільніший з них визначає асимптотичну поведінку всієї програми. Двоє вкладених циклів, за якими слідує одиничний цикл, асимптотично дорівнюються просто двом вкладеним циклам, тому що вкладені цикли домінують над одиничним.
Тепер перейдемо до незвичного способу запису, що використовується теоретиками. Коли ми виводимо асимптотичну поведінку, ми можемо сказати, що наша програма — це Θ( f( n ) ). Наприклад, програми вище — це, відповідно, Θ( 1 ), Θ( n2 ) та Θ( n2 ). Θ( n ) вимовляється як «тета від ен». Іноді ми говоримо, що f( n ), початкова функція підрахунку команд, яка містить константи, — це Θ( щось ). Наприклад, можна сказати, що функція f( n ) = 2n — це Θ( n ). Ще один варіант запису: 2n ∈ Θ( n ), вимовляється як "два ен це тета від ен". Не треба ніяковіти, адже цей запис лише говорить: ми підрахували кількість команд, які виконуються програмою, і вона дорівнює 2n; тобто асимптотичну поведінку алгоритму можна описати як n (опустивши константу 2). Наступні математичні вирази використовують новий спосіб запису:
- n6 + 3n ∈ Θ( n6 )
- 2n + 12 ∈ Θ( 2n )
- 3n + 2n ∈ Θ( 3n )
- nn + n ∈ Θ( nn )
До речі, це і є відповіді до вправи 1.
Ми називаємо цю функцію — я маю на увазі ту функцію, котру ми маємо Θ( тут ) — часовою складністю або просто складністю алгоритму. Так, алгоритм із Θ( n ) має складність n. У нас також є спеціальні назви для Θ( 1 ), Θ( n ), Θ( n2 ) та Θ( log( n ) ), бо це розповсюдженні класи складності. Алгоритм із Θ( 1 ) має назву алгоритм сталого часу, Θ( n ) — лінійний алгоритм, Θ( n2 ) — квадратичний, Θ( log( n ) ) — логарифмічний (не турбуйтеся, якщо ви не знайомі з останнім терміном, логарифми будуть розглянуті трохи нижче).
Підказка: Чим більше Θ, тим повільніше працює програма.

«O» велике
Насправді іноді нелегко визначити поведінку алгоритму, використовуючи даний вище підхід. Особливо це стосується більш складних прикладів. Хай там як, завжди можливо оцінити діапазон поведінки алгоритму. Це полегшує нам життя, оскільки звільняє від необхідності визначати точну швидкість роботи алгоритму. Все, що нам необхідно зробити — це визначити межі поведінки алгоритму. Цей підхід роз'яснюється в наступному прикладі.
Для навчання алгоритмам зазвичай використовується задача сортування. У цьому завданні дається масив A з розміром n (звучить знайомо?), і нас просять написати програму, яка впорядковує елементи масиву. Це цікаве завдання: воно має практичне застосування в реальних системах. Наприклад, менеджер файлів повинен впорядкувати файли за назвою, для спрощення навігації користувача. Або інший приклад: відеогрі необхідно впорядкувати 3D об'єкти світу на підставі їх розташування щодо гравця, для визначення, які з об'єктів видимі, а які ні (розрахунок області видимості, дивіться Ілюстрацію 3). Найближчі до гравця об'єкти будуть видимі, а більш віддалені можуть бути приховані об'єктами між ними. Сортування стає ще цікавішим через наявність різних за ефективністю алгоритмів сортування. І, нарешті, це досить доступне для пояснення та розуміння завдання. Так що і ми зараз напишемо код сортування масиву.
Далі показаний неефективний спосіб реалізації сортування масиву, написаний на мові Ruby. (Звичайно ж, Ruby надає вбудовані функції для сортування масиву, які й слід використовувати в більшості випадків. Вбудовані функції працюють швидше, ніж показана нижче програма, запропонована суто для ілюстрації).
b = []
n.times do
m = a[ 0 ]
mi = 0
a.each_with_index do |element, i|
if element < m
m = element
mi = i
end
end
a.delete_at( mi )
b << m
end
Такий метод називається сортування вибором (англ. selection sort). Сортування вибором знаходить найменше значення масиву (ми позначили масив як a, мінімальне значення m, індекс цього значення mi), додає знайдене значення до кінця масиву b і видаляє це значення з заданого масиву a. Потім алгоритм знову знаходить мінімальне значення серед решти елементів масиву a, додає його до кінця масиву b (тепер масив b містить два відсортованих елемента) та видаляє з масиву a. Перелічені кроки повторюються, доки початковий масив не стане порожнім, а всі його елементи виявляться перенесеними в новий, відсортований, масив. Цей приклад містить вкладені цикли. Зовнішній цикл відпрацьовує n раз, а внутрішній масив відпрацьовує один раз для кожного елемента масиву a. Спочатку масив a містить n елементів, проте ми видаляємо з нього один елемент на кожному кроці зовнішнього циклу. Так що внутрішній цикл відпрацьовує n разів під час першого кроку зовнішнього циклу, потім n - 1 разів, потім n - 2 разів і так далі, до останнього кроку зовнішнього циклу, на якому внутрішній цикл відпрацює лише один раз.
Оцінити складність цієї програми трохи важче, позаяк нам треба підрахувати суму 1 + 2 + ... + (n - 1) + n. Але ми точно можемо знайти «верхню межу» для цієї програми. Адже ми можемо змінити нашу програму (ви можете виконати цю операцію в умі, без написання коду) таким чином, щоб вона стала гіршою, ніж вона є насправді, а потім знайти складність такої виведеної програми. Якщо ми знайдемо складність виведеної програми, то складність початкової програми буде такою ж або навіть меншою. Тобто, якщо виявиться, що виведена програма досить ефективна (ця ефективність за визначенням гірша, ніж у початкової програми), то ми зможемо зробити висновок, що початкова програма теж має гарну ефективність. Принаймні не меншу (або навіть більшу), ніж у виведеної — погіршеної — програми.
А зараз поміркуємо про засіб редагування програми з прикладу таким чином, щоб спростити оцінку її складності. При цьому майте на увазі, що ми можемо змінювати програму лише в бік погіршення, тобто робити так, щоб вона виконувала ще більше команд (аби оцінка складності правильно співвідносилася з початкової програмою). Очевидно, що ми можемо змінити кількість кроків, які виконуються внутрішнім циклом програми так, щоб їх завжди було точно n, замість зменшення кількості кроків. Деякі з цих повторень будуть марними для сортування, але спростять нам аналіз складності алгоритму. Якщо ми зробимо цю просту зміну, тоді новий, тільки що сконструйований, алгоритм буде оцінюватися як Θ( n2 ), тому що він буде складатися з двох вкладених циклів, кожен з яких повторюється n разів. У такій ситуації ми говоримо, що початковий алгоритм має складність O( n2 ). O( n2 ) вимовляється як «велике о від ен у квадраті». Це означає, що наша програма асимптотично не гірша, ніж n2 (вона може навіть бути кращою або дорівнювати n2). Між іншим, якщо наша програма насправді має складність Θ( n2 ), то це також відповідає O( n2 ). Щоб допомогти вам це зрозуміти, уявіть, як ви змінюєте початкову програму зовсім трішечки, але все ж погіршує її продуктивність, наприклад додавши несуттєву команду на початку програми. Таким чином ви зміните функцію підрахунку команд на константу, ігноровану при визначенні асимптотичної поведінки. Звідси випливає, що програма Θ( n2 ) також є O( n2 ).
А ось програма зі складністю O( n2 ) може не мати Θ( n2 ). Наприклад, будь‐яка програма з Θ( n ) — це також O( n2 ), на додачу до O( n ). Уявімо, що програма Θ( n ) — це простий цикл for, що повторюється n разів. Тоді можна погіршити її, обернувши в другий цикл for, такий, що теж повторюється n разів, і отримати у результаті програму з f( n ) = n2. Узагальнимо: будь‐яка програма зі складністю Θ( a ) також має складність O( b ), якщо b зростає швидше за a. Зверніть увагу, що зміни, внесені в програму, не повинні привести до справної програми або програми, аналогічній початковій. Їй тільки необхідно виконувати більше команд, ніж виконується оригінальною версією програми. Змінену програму ми використовуємо суто для підрахунку команд, а не для розв'язання початкової задачі.
Отже, безпечніше буде сказати, що наша програма має складність O( n2 ): ми проаналізували алгоритм і знайшли, що він ніколи не працює гірше, ніж n2. Таке формулювання дає нам достатню оцінку швидкості роботи нашої програми. Наступні вправи дано для звикання до нової нотації.
Вправа 3
Визначте вірні формулювання:
- Алгоритм з Θ( n ) має складність O( n )
- Алгоритм з Θ( n ) має складність O( n2 )
- Алгоритм з Θ( n2 ) має складність O( n3 )
- Алгоритм з Θ( n ) має складність O( 1 )
- Алгоритм з O( 1 ) має складність Θ( 1 )
- Алгоритм з O( n ) має складність Θ( 1 )
Відповіді
- Вірно, бо початкова програма має складність Θ( n ). Ми можемо отримати O( n ) навіть не змінюючи програму.
- Вірно, бо n2 гірше, ніж n.
- Вірно, адже n3 гірше, ніж n2.
- 1 не гірше, ніж n, тож це невірне твердження. Якщо програма асимптотично виконує n команд (лінійна кількість), то ми не можемо ускладнити її та отримати лише одну команду, виконувану асимптотично (стала кількість).
- Вірно, бо ці складності рівнозначні.
- Це може бути як вірним, так і невірним твердженням. У загальному випадку воно хибне. Якщо алгоритм має складність Θ( 1 ), тоді він зазвичай має й складність O( n ). Але при O( n ), він не обов'язково буде мати складність Θ( 1 ). Наприклад, алгоритм Θ( n ) має складність O( n ), але не Θ( 1 ).
Вправа 4
Скористайтеся формулою суми арифметичної прогресії для доказу, що дана вище програма має складність не тільки O( n2 ), а й також Θ( n2 ). Якщо ви не знаєте, що таке арифметична прогресія, загляньте у Вікіпедію — це легко.
Оскільки «О» велике алгоритму описує верхню межу дійсної складності алгоритму (що визначається з Θ), то іноді можна сказати, що Θ описує точні межі складності. Якщо відомо, що знайдена межа складності не є точною, то в таких випадках можна використовувати нотацію «o» маленьке. Наприклад, якщо алгоритм має складність Θ( n ), тоді його точна складність відповідає n. Отже, цей алгоритм має складність і O( n ), і O( n2 ). Межа O( n ) є точною, але межа O( n2 ) — ні. Так що можна написати, що цей алгоритм має складність o( n2 ) — вимовляється «o маленьке від ен у квадраті» — для ілюстрації того, що ця межа неточна. Зазвичай краще знати точні межі алгоритмів, адже таким чином більше стає відомо про поведінку алгоритму. Однак точні межі не завжди легко визначити.
Вправа 5
Визначте, які з перелічених меж точні, а які ні. Перевірте, чи всі межі вірні. Використайте «О» велике для ілюстрації неточних меж.
- Алгоритм з Θ( n ) та верхньою межею O( n ).
- Алгоритм з Θ( n2 ) та верхньою межею O( n3 ).
- Алгоритм з Θ( 1 ) та верхньою межею O( n ).
- Алгоритм з Θ( n ) та верхньою межею O( 1 ).
- Алгоритм з Θ( n ) та верхньою межею O( 2n ).
Відповіді
- У цьому випадку Θ й O складності однакові, так що це точна межа.
- Тут ми бачимо, що O дає більшу складність, ніж Θ, так що ця межа неточна (складність O( n2 ) дала б точну межу). Отже, ми можемо записати складність алгоритму у вигляді o( n3 ).
- Ми знову бачимо, що O дає більшу складність, ніж Θ. Так що це неточна межа (межа O( 1 ) була б точною). Отже, можна позначити, що межа O( n ) неточна, записавши її у вигляді o( n ).
- Ця межа помилкова. Для алгоритму з Θ( n ) неможливо, щоб верхня межа була O( 1 ), адже n має більшу складність, ніж 1. Пам'ятайте, що «О» велике описує верхню межу.
- Може здатися, що ця межа неточна, однак це не так. Ця межа насправді точна. Згадайте, що асимптотична поведінка 2n є n; а також що O й Θ описуюсь асимптотичну поведінку. З цього випливає, що O( 2n ) = O( n ), тобто ця межа точна, бо вона дорівнює Θ.
Підказка: Знайти складність «O» легше, ніж складність «Θ».
Ймовірно, що всі ці нові форми запису добряче вас вже притомили. Все ж познайомимося ще з двома символами, а потім розглянемо приклади. Ці символи буде легко зрозуміти на базі вже знайомих вам Θ, O та o. Нові символи не будуть вживатися в наступній частині статті, проте добре б їх знати; зараз відповідний момент для такого знайомства. В наведеному вище прикладі, ми змінювали програму так, щоб вона працювала гірше (додавши команди для уповільнення її роботи), і виводили таким чином «О» велике. «O» надає цінну інформацію, на базі якої можна доводити, що наша програма працює досить добре. Якщо виконати зворотну дію: поліпшити програму, щоб потім знайти її складність; теж можна використовувати форму запису «Ω». Ω описує складність таким чином, що ми знаємо: наша програма не працюватиме краще цієї складності. Таке знання корисно в тих випадках, коли ми хочемо показати, що програма працює повільно або що аналізований алгоритм не є ефективним для розв'язання певної задачі. Наприклад, алгоритм зі складністю Ω( n3 ) означає, що цей алгоритм не працює краще, ніж n3 (він як мінімум настільки поганий). Тобто цей алгоритм може мати складність Θ( n3 ), або Θ( n4 ), або навіть гірше. Отже, Ω дає нам нижню межу складності алгоритму. На зразок «ο» маленького, можна використовувати запис у вигляді «ω» маленьке тоді, коли відомо, що межа неточна. Наприклад, алгоритм Θ( n3 ) має ο( n4 ) та ω( n2 ). Ω( n ) вимовляється як «омега велике від ен», а ω( n ) вимовляється як «омега маленьке від ен».
Вправа 6
Визначте точні та неточні О і Ω межі наступних Θ складностей.
- Θ( 1 )
- Θ(
 )
) - Θ( n )
- Θ( n2 )
- Θ( n3 )
Відповіді
- Точними межами є O( 1 ) і Ω( 1 ). Неточною O межею може бути O( n ). Згадайте, що O дає нам верхню межу. n має більшу складність, ніж 1, тож цю неточну межу можна також записати як o( n ). Неточна Ω межа не існує, бо не можливо спростити складність, що дорівнює 1.
- Точні межі дорівнюються Θ складності, так що це O(
 ) та Ω(
) та Ω(  ). В ролі неточної межі можна використовувати O( n ), адже n більше, ніж
). В ролі неточної межі можна використовувати O( n ), адже n більше, ніж  . Знаючи, що це неточна верхня межа, можна використати форму запису o( n ). Для неточної нижньої межі можна використати Ω( 1 ), що також можна записати як ω( 1 ).
. Знаючи, що це неточна верхня межа, можна використати форму запису o( n ). Для неточної нижньої межі можна використати Ω( 1 ), що також можна записати як ω( 1 ). - Точними межами є O( n ) і Ω( n ). Неточними межами можуть бути ω( 1 ) та o( n3 ). Але це досить поганий вибір меж, бо вони сильно відрізняються від початкової складності. Однак вони відповідають даними нами визначенням, тож їх можна використовувати.
- Точними межами є O( n2 ) і Ω( n2 ). В ролі неточних меж можна знову використати ω( 1 ) та o( n3 ), як і в попередньому прикладі.
- Точними межами є O( n3 ) і Ω( n3 ). Неточними межами можуть бути ω(
 n2 ) та o(
n2 ) та o(  n3 ). Це неточні межі, але все одне вони кращі за ті, що були дані вище.
n3 ). Це неточні межі, але все одне вони кращі за ті, що були дані вище.
Причина використання O і Ω замість Θ — хоча O і Ω також можуть визначати точні межі — полягає в тому, що не завжди відомо, чи є знайдена межа точної (ймовірно, коли в нас нема бажання прискіпливо аналізувати алгоритм).
Не хвилюйтеся, якщо ви не запам'ятали всі символи та їх призначення. Ви завжди можете повернутися до цієї статті й уточнити їх дані. Найважливішими символами є O і Θ.
Також зауважте, що хоча Ω визначає поведінку нижньої межі функції (тобто функція була поліпшена зменшенням кількості виконуваних команд), ми все ще посилаємося на аналіз «найгіршого випадку». Так відбувається тому, що ми даємо програмі самий поганий варіант із можливих вхідних даних; поведінка програми аналізується виходячи з цього припущення.
Наступна таблиця показує тільки що представлені символи та відповідні їм звичайні математичні символи, використовувані для порівняння чисел. Літери грецького алфавіту використовуються замість більш звичних символів для вказівки, що ми займаємося порівнянням асимптотичної поведінки, а не чисел.
| Асимптотичне порівняння | Чисельне порівняння |
|---|---|
| Алгоритм з o( щось ) | Число < щось |
| Алгоритм з O( щось ) | Число ≤ щось |
| Алгоритм з Θ( щось ) | Число = щось |
| Алгоритм з Ω( щось ) | Число ≥ щось |
| Алгоритм з ω( щось ) | Число > щось |
Підказка: Хоча всі символи O, o, Ω, ω і Θ дуже корисні, «О» велике використовується найчастіше. Його простіше визначити, ніж Θ, й воно практичніше, ніж Ω.
Логарифми
Якщо ви знаєте, що таке логарифм, то можете пропустити цей розділ. Цей ознайомчий розділ написаний для тих, хто не знайомий із логарифмами; а також для тих, хто давно з ними не стикався. Цей текст також призначений для учнів, які ще не вивчали логарифми в школі. Знання логарифмів дуже важливе, адже вони постійно зустрічаються при аналізі складності алгоритмів. Логарифм — це операція, застосована до числа так, що число значно зменшується (зовсім як витяг кореня). Витяг квадратного кореня є операцією, зворотною від піднесення числа до квадрату. Так саме, логарифм — це зворотна операція від піднесення числа до будь-якого степеня. Насправді все набагато простіше, ніж звучить. Краще розглянемо на ось такому прикладі:
2x = 1024
Для того, щоб розв'язати це рівняння та знайти значення x, ми запитуємо себе: в яку степінь потрібно звести 2, щоб отримати 1024? Це буде число 10. Дійсно, ми отримуємо 210 = 1024, що легко підтвердити. Логарифми допомагають записати цю задачку в інший нотації. В цьому випадку 10 є логарифмом 1024, що записується як log( 1024 ) (вимовляється як «логарифм 1024»). Позаяк ми використовуємо 2 в основі логарифмів, такі логарифми мають назву двійкових. Існують логарифми з іншими основами, але в цій статті ми використовуємо лише логарифми з основою 2. Якщо ви учень, який бере участь у міжнародних змаганнях і не знайомий з логарифмами, то я вкрай рекомендую вам попрактикуватися після прочитання цієї статті. В інформатиці двійкові логарифми зустрічаються частіше, ніж інші типи логарифмів. Все через те, що в інформатиці ми в базі маємо лише дві сутності: 0 та 1; і воліємо розбивати великі проблеми на дві частини (повторюючи цю дію). Отже, для подальшого читання статті вам необхідні тільки двійкові логарифми.
Вправа 7
Розв'яжіть рівняння. Запишіть знайдені логарифми. Використовуйте тільки двійкові логарифми.
- 2x = 64
- (22)x = 64
- 4x = 4
- 2x = 1
- 2x + 2x = 32
- (2x) * (2x) = 64
Відповіді
Просто використовуйте ідеї, дані вище.
- Методом проб і помилок знаходимо, що x = 6 і log( 64 ) = 6.
- Згідно з властивостями степеня, (22)x можна записати як 22x. Застосовуючи попередній результат log( 64 ) = 6, ми отримуємо, що 2x = 6. Отже, x = 3.
- Використовуючи дані з попереднього рівняння, можна записати 4 у вигляді 22, так що рівняння перетворюється в (22)x = 4, а це те ж саме, що 22x = 4. Потім ми помічаємо, що log( 4 ) = 2 (адже 22 = 4) і, отже, ми отримуємо, що 2x = 2. Тобто x = 1. Цей результат легко підтвердити, бо піднесення числа до степеня 1 повертає само число.
- Згадаймо, що піднесення числа до степеня 0 дає в результаті 1. Значить, 20 = 1, тобто x = 0 і log( 1 ) = 0.
- Тут ми маємо справу зі складанням, так що не можемо визначити логарифм безпосередньо. Однак ми помічаємо, що 2x + 2x дорівнюється 2 * (2x). Отже, у нас з'явився множник 2, тоді цей вираз можна записати у вигляді 2x + 1. Тепер нам залишилося тільки розв'язати рівняння 2x + 1 = 32. Ми знаходимо, що log( 32 ) = 5 і тоді x + 1 = 5. Отже, x = 4.
- Ми множимо результати піднесення 2 до степеня x, тобто ми можемо об'єднати множники, помітивши, що (2x) * (2x) дорівнюється 22x. Потім усе, що нам треба зробити — це розв'язати рівняння 22x = 64, яке ми вже розв'язували з результатом x = 3.
Підказка: У випадку з алгоритмами, написаними для змагань (на мові C ++), як тільки складність була проаналізована, можна отримати орієнтовну оцінку швидкості роботи вашої програми. Чекайте продуктивність близько 1,000,000 операцій в секунду (для операцій, кількість яких визначено функцією асимптотичної поведінки алгоритму). Наприклад, алгоритм зі складністю Θ (n) відпрацьовує приблизно за секунду при розмірі вхідних даних n = 1,000,000.
Складність рекурсивних алгоритмів
Розглянемо рекурсивні функції. Рекурсивною називається функція, яка викликає саму себе. Чи піддається аналізу складність таких функцій? Наступна функція, написана на мові Python, обчислює факторіал числа. Факторіал позитивного цілого числа знаходиться за допомогою множення початкового числа з кожним попереднім йому позитивним цілим числом. Наприклад, факторіал числа 5 дорівнює 5 * 4 * 3 * 2 * 1. Факторіал записується у вигляді «5!», що вимовляється як «п'ять факторіал» (хоча деякі люди полюбляють голосно викрикувати «П'ЯТЬ!!!»)
def factorial( n ):
if n == 1:
return 1
return n * factorial( n - 1 )
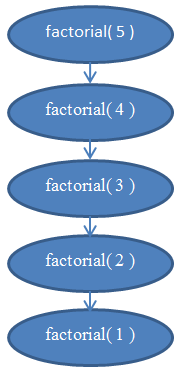
Проаналізуємо складність цієї функції. Вона не містить циклів, але її складність все ж не є сталим значенням. Для визначення складності нам треба знову зайнятися підрахунком команд, які виконуються програмою. Очевидно, що якщо передати в цю програму деяке значення n, то вона відпрацює n разів. Якщо ви не впевнені в цьому, то перевірте «вручну», яким чином функція відпрацює при n = 5. Ви побачите, що функція буде викликана 5 разів, кожен раз зменшуючи n на 1. Отже, функція має складність Θ( n ).
Якщо ви все ще не впевнені в цьому факті, згадайте, що завжди можна знайти точну складність, підрахувавши кількість виконуваних команд. Якщо хочете, спробуйте підрахувати реальну кількість команд, які виконуються функцією факторіала, виведіть f (n) і переконайтеся, що вона на ділі лінійна (нагадую, що лінійна функція відповідає Θ (n)).
Ілюстрація 5 містить діаграму, яка допоможе вам зрозуміти, як виглядає рекурсія при виконанні функції factorial (5), і чому ця функція має лінійну складність.
Логарифмічна Складність
Одна з класичних задач в інформатиці — це пошук значення в масиві. Ми вже стикалися з таким завданням в одному з попередніх розділів. Пошук у масиві стає дуже цікавим, якщо нам дано вже відсортований масив. Один зі способів пошуку у відсортованому масиві називається двійковим. При такому способі перевіряється елемент у середині масиву: якщо знайдено шукане значення, то пошук закінчений; якщо значення середини більше, ніж шукане, то пошук продовжується в лівій частині масиву; інакше пошук продовжується в правій частині масиву. Потім отримані менші масиви знову розбиваються навпіл, доки не залишиться лише один елемент. Ось цей метод записаний за допомогою псевдокоду:
def binarySearch( A, n, value ):
if n = 1:
if A[ 0 ] = value:
return true
else:
return false
if value < A[ n / 2 ]:
return binarySearch( A[ 0...( n / 2 - 1 ) ], n / 2 - 1, value )
else if value > A[ n / 2 ]:
return binarySearch( A[ ( n / 2 + 1 )...n ], n / 2 - 1, value )
else:
return true
Цей псевдокод є спрощеною версією реальної реалізації двійкового пошуку. На практиці двійковий пошук легше описати, ніж реалізувати в коді. Адже програмістам треба подбати про всі деталі: помилку неврахованої одиниці (англ. off-by-one error), необхідності округлення результатів розподілу на 2 і таке інше. Ми лише бажаємо проаналізувати складність цього алгоритму, тому припустимо, що він завжди працює успішно, і що реальна імплементація подбає про всі необхідні деталі. Якщо ви ніколи не реалізовували двійковий пошук, рекомендую зробити це на вашій улюбленій мові програмування. Це дійсно просвітницьке зайняття.
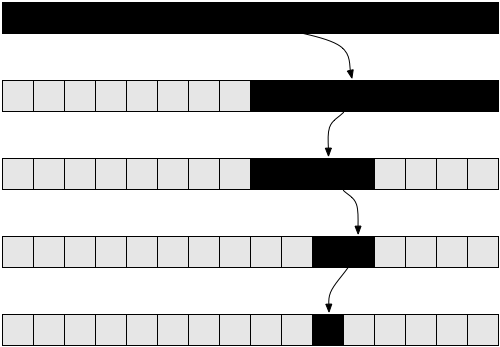
Ілюстрація 6 повинна допомогти вам зрозуміти, як працює двійковий пошук.
Якщо ви не впевнені в працездатності цього методу, візьміть простий приклад і переконайтеся, що він дійсно працює.
Зараз спробуємо проаналізувати цей алгоритм. Тут ми знову зіткнулися з рекурсією. Припустимо для простоти, що масив завжди ділиться рівно навпіл, і проігноруймо + 1 і - 1 у рекурсивних викликах. Ви вже повинні розуміти, що така маленька зміна, як ігнорування + 1 і - 1, не вплине на результати аналізу складності. Нам довелося б доводити цей факт, якби ми хотіли бути точними з математичної точки зору, але він і так інтуїтивно зрозумілий. Також для простоти припустимо, що нам дано масив із розміром, що дорівнює степеню 2. Це припущення теж не вплине на кінцевий результат аналізу складності. Найгірший випадок цього завдання буде отримано, якщо шуканого значення взагалі немає в масиві. В такому випадку при першому виклику функції алгоритм отримає масив із розміром n. При наступному, рекурсивному, виклику: n / 2. Після цього рекурсивний виклик отримає масив із розміром n / 4, потім масив із розміром n / 8 і так далі. Масив розбивається навпіл при кожному новому рекурсивному виклику, поки не досягне розміру 1. Отже, запишемо кількість елементів масиву при кожному виклику:
Зверніть увагу, що на i-му кроці масив має n / 2i елементів. Так відбувається тому, що на кожному кроці масив поділяється навпіл (іншими словами, ми ділимо кількість елементів масиву на 2). Цю дію можна виразити у вигляді множення знаменника на 2. Роблячи таку операцію i разів, отримуємо n / 2i. Потім процедура розподілу триває, для все більшого i ми отримуємо все меншу кількість елементів, доки не досягнемо останнього кроку, на якому залишається лише 1 елемент. Якщо ми хочемо знайти i, щоб дізнатися кількість кроків роботи програми, необхідно знайти рішення наступного рівняння:
1 = n / 2i
Це рівняння стане вірним лише тоді, коли ми доберемося до останнього виклику функції binarySearch(), не в загальному випадку. Знайшовши i, ми знайдемо, на якому етапі закінчаться рекурсивні виклики. Помноживши обидві сторони на 2i, отримуємо:
2i = n
Це рівняння має виглядати знайомим, якщо ви прочитали розділ про логарифми. Розв'язавши рівняння для i, отримуємо:
i = log( n )
Цей вираз показує нам, що кількість кроків, необхідних для здійснення двійкового пошуку, дорівнюється log( n ), де n — кількість елементів у масиві.
Такий результат виглядає цілком реалістично. Наприклад, візьміть n = 32, масив із 32 елементами. Скільки разів нам доведеться ділити масив навпіл, щоб отримати 1 елемент? Ми отримаємо: 32 → 16 → 8 → 4 → 2 → 1 елементів, виконавши 5 кроків, що і є логарифм 32. Отже, складність двійкового пошуку дорівнює Θ( log( n ) ).
Останній результат дозволяє нам порівняти двійковий пошук із лінійним пошуком (попередній з розглянутих нами методів). Очевидно, що log (n) набагато менший, ніж n; тож ми робимо висновок, що двійковий пошук шукає елементи в масиві набагато швидше, ніж лінійний пошук. Також можна порекомендувати підтримувати масиви відсортованими, якщо необхідно часто здійснювати пошук у них.
Підказка: Поліпшення асимптотичного часу роботи програм також часто значно покращує їх час роботи. І в набагато більших масштабах, ніж будь-які дрібні «технічні» оптимізації, як, наприклад, використання більш швидкої мови програмування.
Оптимальне сортування
Вітаю. Тепер ви знаєте, що таке аналіз складності алгоритмів, асимптотична поведінка й «О» велике. Тепер ви знаєте, що таке складність алгоритму O( 1 ), O( log( n ) ), O( n ), O( n2 ) і так далі. Ви розумієте значення символів o, O, ω, Ω і Θ, а також що таке аналіз найгіршого випадку. Раз ви дісталися до цього етапу, значить навчальний матеріал впорався зі своїм завданням.
Цей фінальний розділ необов'язковий для прочитання. Він складніший, так що можете опустити його, якщо відчуєте, що ви перевантажені. Цей розділ потребує від вас фокусування для опрацювання додаткових вправ. При цьому, він покаже вам дуже корисний і потенційно потужний метод аналізу складності алгоритмів, що може стати вартим вкладання ваших сил.
Вище ми розглядали реалізацію алгоритму під назвою сортування вибором. Було згадано, що сортування вибором не є оптимальним алгоритмом. Оптимальним називається алгоритм, який вирішує завдання найкращим способом. Це означає, що всі інші алгоритми розв'язання цієї ж задачі мають складність гіршу чи таку ж, як у оптимального алгоритму. Для розв'язання задач певної складності існує безліч оптимальних алгоритмів. Зокрема, завдання сортування можна вирішити оптимально різними способами. Наприклад, можна використати ідею, що лежить в основі двійкового пошуку, щоб отримати швидкий спосіб сортування, який називається сортування злиттям (англ. merge sort).
Щоб виконати сортування злиттям, спочатку необхідно написати допоміжну функцію, яка буде використана під час самого сортування. Ми створимо функцію merge. Ця функція приймає два відсортованих масивів і з'єднує (англ. merge: злиття) їх разом, в один упорядкований масив. Це легко зробити:
def merge( A, B ):
if empty( A ):
return B
if empty( B ):
return A
if A[ 0 ] < B[ 0 ]:
return concat( A[ 0 ], merge( A[ 1...A_n ], B ) )
else:
return concat( B[ 0 ], merge( A, B[ 1...B_n ] ) )
Функція concat приймає елемент («голову») та масив («хвіст»), потім будує і повертає новий масив, що містить «голову» на першій позиції нового масиву, а елементи «хвоста» на решті позицій масиву. Наприклад, concat( 3, [ 4, 5, 6 ] ) повертає [ 3, 4, 5, 6 ]. Ми використовуємо A_n і B_n для позначення розмірів масиву A та B.
Вправа 8
Перевірте, що дана вище функція дійсно виконує злиття. Перепишіть її на своїй улюбленій мові програмування, використовуючи цикл for замість рекурсії.
Аналіз цього алгоритму показує, що час його виконання Θ( n ), де n є розміром кінцевого масиву (n = A_n + B_n).
Вправа 9
Перевірте, що час роботи функції merge merge є Θ( n ).
Використовуючи цю функцію, можна побудувати покращений алгоритм сортування. Базова ідея: ділити масив на дві частини. Ми сортуємо кожну з двох частин рекурсивно, а потім об'єднуємо два впорядковані масиви в один великий масив. Псевдокод:
def mergeSort( A, n ):
if n = 1:
return A # впорядкований масив
middle = floor( n / 2 )
leftHalf = A[ 1...middle ]
rightHalf = A[ ( middle + 1 )...n ]
return merge( mergeSort( leftHalf, middle ), mergeSort( rightHalf, n - middle ) )
Цю функцію складніше зрозуміти, ніж те, що ми вже розглядали, отже для наступної вправи може знадобитися більше часу.
Вправа 10
Перевірте, що функція mergeSort працює вірно. А саме, що вона дійсно сортує даний їй масив. Якщо ви не розумієте, як ця функція працює, то візьміть маленький масив і відстежте «вручну» кроки, виконувані mergeSort. При цьому ви переконаєтеся, що leftHalf і rightHalf утворюються при розбитті масиву приблизно посередині; розбиття не обов'язково відбувається точно в центрі масиву, якщо він містить непарну кількість елементів (з цієї причини використовується функція floor).
Як останній приклад, піддамо аналізу складність mergeSort. На кожному етапі виконання mergeSort, масив розбивається на дві частини однакового розміру, зовсім як при binarySearch. Однак у разі сортування обидві частини зберігаються в процесі виконання програми. Алгоритм застосовується рекурсивно до кожної з частин. До результату виконання рекурсій застосовується операція merge, яка займає Θ( n ) часу.
Отже, ми розбиваємо початковий масив на два масиви, кожен із розміром n / 2. Потім ми об'єднуємо ці нові масиви, і ця дія об'єднання n елементів вимагає Θ (n) часу.
Гляньте на Ілюстрацію 7, щоб краще зрозуміти, що відбувається.
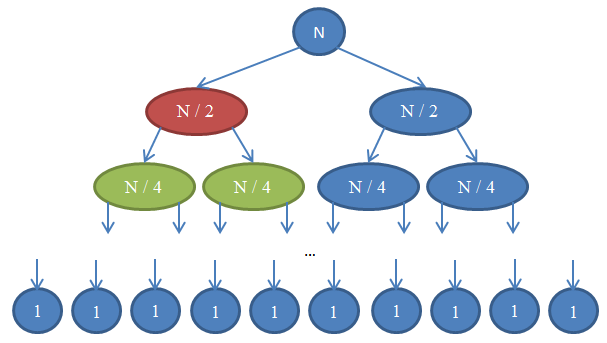
Подивимося, що тут відбувається. Кожне коло відображає виклик функції mergeSort. Число всередині кола показує розмір сортованого масиву. Верхнє синє коло — це початковий виклик mergeSort, із завданням впорядкувати масив із розміром n. Стрілки показують рекурсивні виклики функції. Початковий виклик mergeSort робить два рекурсивних запита до mergeSort, передаючи кожного разу один масив із розміром n / 2. Ця дія відображається двома стрілками вгорі картинки. Своєю чергою, кожен із викликів функції робить ще два виклики mergeSort, передаючи кожного разу масив із розміром n / 4 і так далі, поки не будуть отримані масиви з одним елементом. Така схема називається рекурсивним деревом, тому що вона відображає послідовність рекурсивних викликів і схожа на дерево (точніше на перевернуте дерево, корінь якого розташований вгорі, а листя — внизу).
Зверніть увагу, що в кожнім ряду схеми загальна кількість елементів завжди дорівнюється n. Щоб побачити це, розгляньте кожен ряд окремо. Перший ряд містить тільки один виклик mergeSort із масивом, який має розмір n, так що загальна кількість елементів дорівнюється n. Другий ряд містить два виклики mergeSort, де кожен із масивів має розмір n / 2. Але n / 2 + n / 2 = n, так що знову загальна кількість елементів у цьому ряду дорівнюється n. У третьому ряду ми бачимо 4 виклики, кожен з яких обробляє масив із розміром n / 4, в результаті даючи загальну кількість елементів n / 4 + n / 4 + n / 4 + n / 4 = 4n / 4 = n. Отже, знову ми отримуємо n елементів. Тепер зверніть увагу, що в кожнім ряду схеми функція, яка робить виклик, повинна буде виконати операцію merge з поверненими елементами. Наприклад, коло, позначене червоним кольором, повинно впорядкувати n / 2 елементів. Щоб зробити це, воно розбиває масив із розміром n / 2 на два масиви з розміром n / 4, викликає рекурсивно mergeSort для їх сортування (ці виклики відображені колами зеленого кольору), потім об'єднує результати в один масив. Операція об'єднання працює з n / 2 елементами. В кожнім ряду дерева загальна кількість поєднуваних елементів дорівнює n. У щойно розглянутому ряду функція об'єднує n / 2 елементів; функція праворуч від неї (показана синім кольором) теж об'єднує n / 2 елементів. Разом маємо n об'єднаних елементів у аналізованому ряду схеми.
Відповідно до цих міркувань, кожен ряд має складність Θ (n). Нам відомо, що кількість рядів — відома під назвою глибина дерева рекурсії — у схемі дорівнюється log( n ). Це виводиться так само як було зроблено під час аналізу складності двійкового пошуку. Маючи кількість рядів log (n), при тому, що кожен із них має складність Θ (n), складність mergeSort дорівнюється Θ( n * log( n ) ). Це набагато кращий результат, ніж Θ( n2 ), який ми отримуємо при сортуванні вибором (нагадую, що значення log( n ) набагато менше, ніж n; так що n * log( n ) набагато менше, ніж n * n = n2). Якщо все це звучить занадто складно для вас, не турбуйтеся: таку інформацію непросто зрозуміти з першого разу; прочитайте цей розділ ще раз після того, як ви самі спробуєте реалізувати сортування злиттям і переконаєтеся, що воно працює.
Як було показано в останньому прикладі, аналіз складності дозволяє нам порівнювати алгоритми між собою для з'ясування, який з них працює краще. Тепер ми цілком впевнені, що для великих масивів даних сортування злиттям працює швидше, ніж сортування вибором. Прийти до цього висновку було б важко без теоретичних знань, представлених у цій статті та необхідних для аналізу алгоритмів. На практиці дійсно використовують алгоритми сортування з часом роботи Θ (n * log (n)). Наприклад, ядро Linux використовує алгоритм під назвою пірамідальне сортування (англ. heapsort), з тим же часом роботи, що й у сортування злиттям, розглянутого нами — а саме Θ( n log( n ) ) — і який є оптимальним алгоритмом. Зверніть увагу: ми не доводили, що ці алгоритми оптимальні. Для цього нам знадобилася б складніша математична аргументація. Однак можу вас запевнити, що з точки зору складності алгоритмів, сортування не можна зробити більш ефективним.
Знання про аналіз складності алгоритмів, які ви придбали під час читання цієї статті, повинні допомогти вам створювати швидші програми й фокусувати зусилля, прикладені для оптимізації коду, на дійсно значущих речах; таким чином роблячи вас продуктивнішим. Також, математичну мову та позначення, з якими ви познайомилися у цій статті, допоможуть вам при спілкуванні з іншими програмістами. Тепер ви зможете обговорювати час роботи алгоритмів, використовуючи отримані знання.
Післяслово
Ця стаття ліцензується з Creative Commons 3.0 Attribution. Це означає, що статтю можна копіювати, поширювати, публікувати на вашому ресурсі, змінювати, та й взагалі робити з нею все, що забажається — при цьому вказавши моє ім'я. Якщо ви базуєте свою статтю на моїй, то ви не зобов'язані, але я вам пропоную також опублікувати ваш текст із ліцензією Creative Commons, щоб іншим людям було легше ділитися та співпрацювати. Відповідно до цього, ось роботи, що я використав: fugue icons, Lea Verou. І, найважливіше, я зміг написати цю статтю завдяки знанням, отриманим від професорів Nikos Papaspyrou і Dimitris Fotakis.
Я являюся PhD кандидатом в області криптографії в Афінському університеті. Коли я писав цю статтю, я був студентом факультету Електротехніки та комп'ютерних наук Афінського національного технічного університету, спеціалізуючись у програмному забезпеченні та бувши тренером з Грецьких змагань в області інформатики. Як програміст практик, я був у команді, що побудувала deviantART, соціальну мережу для художників; у командах безпеки в Google і Twitter; а також у стартапах Zino і Kamibu, які займалися соціальними мережами і розробкою відеоігор. Якщо вам сподобалася стаття, підписуйтесь у Twitter або GitHub. Надішліть e-mail, якщо хочете зв'язатися зі мною або зайнятися перекладом цього тексту.
Дякую вам за читання. Мені не платили за написання цієї статті, тож, якщо вона вам сподобалася, відправте мені e-mail із привітанням. Мені подобається отримувати фотографії з усього світу. Якщо забажаєте, надсилайте ваше фото в місті, де ви живете!
Ресурси
- Cormen, Leiserson, Rivest, Stein. Introduction to Algorithms, MIT Press.
- Dasgupta, Papadimitriou, Vazirani. Algorithms, McGraw-Hill Press.
- Fotakis. Course of Discrete Mathematics at the National Technical University of Athens.
- Fotakis. Course of Algorithms and Complexity at the National Technical University of Athens.

