Uma introdução gentil a análise de complexidade de algoritmos
Dionysis "dionyziz" Zindros <dionyziz@gmail.com>Jefferson Carvalho <jeffersonhcarvalho@gmail.com>
- English
- Ελληνικά
- македонски
- Español
- Nederlands
- עברית
- Português
- srpskohrvatski
- Українська
- Русский
- Help translate
Introdução
Vários dos programadores que fazem alguns dos softwares mais úteis e legais que temos hoje, como muitas coisas que vemos na internet ou usamos no nosso dia a dia, não possuem um conhecimento teórico de ciência da computação. Mesmo assim, eles são programadores excelentes e muito criativos, e agradecemos a eles pelo o que eles construíram.
Entretanto, a parte teórica da ciência da computação tem os seus usos e aplicações, e pode ser bastante prática. Neste artigo, direcionado para programadores que "conhecem a sua arte" mas não tem um background teórico de ciência da computação, irei apresentar uma das ferramentas mais pragmáticas da ciência da computação: a notação Big O e a análise de complexidade de algoritmos. Como alguém que trabalhou tanto na parte acadêmica de ciência da computação quanto no mercado de desenvolvimento de software para produção, essa é uma daquelas ferramentas que eu descobri ser uma das que são realmente úteis na prática, então eu espero que depois de ler este artigo, você possa aplicá-la no seu próprio código para fazê-lo melhor. Depois de ler este post, você deverá ser capaz de entender todos os termos comuns que cientistas da computação usam, como "big O", "comportamento assintótico" e "análise do pior caso".
Este texto também é direcionado para estudantes do ensino médio que competem na Olimpíada Internacional de Informática, uma competição de algoritmos para estudantes, ou outras competições similares. Assim sendo, ele não possui pré-requisitos em matemática e vai te dar a base necessária para que você continue estuando algoritmos com um entendimento mais sólido da teoria por trás deles. Como alguém que participava dessas competições, eu aconselho fortemente que você leia todo este material introdutório e o entenda por completo, porque vai ser necessário quando você estudar algoritmos e aprender técnicas mais avançadas.
Eu acredito que esse texto será útil para programadores da indústria de software que não tem muita experiência com a parte teórica da ciência da computação(é um fato de que alguns dos mais inspiradores engenheiros de software nunca fizeram uma faculdade). Mas pelo fato de que ele também é para estudantes, as vezes ele pode parecer didático demais. Além disso, alguns dos tópicos neste texto podem parecer muito óbvios para você; por exemplo, você deve tê-los visto durante o ensino médio. Se você já conhecer esses assuntos, você pode pulá-los. Outras partes vão ser um pouco mais profundas e se tornar um pouco mais teóricas, pois estudantes que participam dessas competições vão precisar saber mais sobre algorítimos teóricos do que a maioria das pessoas. Mas ainda é interessante saber essas coisas e elas não são muito difíceis de se acompanhar, então é bem provável que valha o seu tempo. Como o texto original foi direcionado para estudantes do ensino médio, nenhum conhecimento prévio de matemática é necessário, então qualquer um com alguma experiência com programação(por exemplo, sabe o que é recursividade) vai ser capaz de acompanhar sem problemas.
Ao longo deste artigo, você encontrará vários ponteiros que vão ligar a materiais interessantes, muitas vezes fora do escopo do tópico em discussão. Se você é um desenvolvedor no mercado, é provável que você já conheça a maioria desses conceitos. Se você é um estudante júnior participando de competições, seguir esses links vai te dar ideias de outras áreas da ciência da computação ou da engenharia de software que você pode ainda não conhecer, e que você pode dar uma olhada para ampliar seus horizontes.
A notação big O e análise de complexidade de algoritmos é algo que tanto programadores no mercado quanto estudantes acham difícil de entender, têm medo ou evitam como se fosse algo inútil. Mas não é tão difícil ou teórico como pode parecer em um primeiro momento. A complexidade de um algoritmo é somente uma maneira de se medir formalmente o quão rápido um programa ou algoritmo pode ser executado, então na verdade é algo bem pragmático. Vamos começar com um pouco de motivação sobre o assunto.

Motivação
Nós já sabemos que existem ferramentas para medir o quão rápido um programa é executado. Existem programas conhecidos como profilers que medem o tempo de execução em milissegundos e podem nos ajudar a otimizar o nosso código encontrando gargalos. Apesar de serem ferramentas úteis, não são tão relevantes para a complexidade de algoritmos. Complexidade de algoritmos é algo feito para comparar dois algoritmos no nível das ideias — ignorando detalhes de baixo nível como a linguagem de programação em que foi implementado, o hardware em que o algoritmo é executado, ou o conjunto de instruções da CPU. Nós queremos comparar algoritmos somente em termos do que eles realmente são: Ideias de como algo é computado. Contar milissegundos não vai nos ajudar nisso. É possível que um algoritmo ruim escrito em uma linguagem de programação de baixo nível como assembly rode muito mais rápido que um bom algoritmo escrito em uma linguagem de alto nível, como Python ou Ruby. Então, é hora de definir o que realmente é um "algoritmo melhor".
Como algoritmos são programas que realizam computações, e não outras coisas que computadores normalmente fazem como tarefas na rede ou entrada e saída de dados, a análise de complexidade nos permite analisar o quão rápido um programa é quando ele realiza uma computação. Exemplos de operações que são puramente computacionais incluem operações de ponto flutuante como adição e multiplicação; pesquisa em uma base de dados que cabe na RAM por um determinado valor; determinar o caminho pelo qual um personagem de inteligência artificial vai caminhar em um vídeo game de tal forma que ele tenha que caminhar apenas uma curta distância dentro do mundo virtual (veja a Figura 1); ou executar um padrão de expressão regular que combine com uma string. Claramente, a computação é ubíqua em programas de computador.
A análise de complexidade também é uma ferramenta que nos permite explicar como um algoritmo se comporta se a entrada aumentar. Se nós precisarmos de um input diferente, como o algoritmo vai se comportar? Se o nosso algoritmo leva 1 segundo para executar para uma entrada de tamanho 1000, como ele vai se comportar se dobrarmos o tamanho da entrada? Ele vai executar tão rápido quanto, vai levar metade do tempo, ou vai ser quatro vezes mais lento? Na prática, isso é importante para nos ajudar a predizer como um algoritmo vai ser comportar se a entrada aumentar. Por exemplo, se fizermos um algoritmo para uma aplicação web que funciona bem com 1000 usuários e medirmos o seu tempo de execução, usando a análise de complexidade nós podemos ter uma boa ideia do que irá acontecer uma vez que tivermos 2000 usuários. Para competições de algoritmos, a análise de complexidade nos dá uma ideia do quão longa será a execução do nosso código para os casos de teste maiores que serão utilizados para testar se o nosso programa está correto. Então, se medirmos o comportamento do nosso programa para uma entrada pequena, nós podemos ter uma boa ideia de como ele vai se comportar com entradas maiores. Vamos começar com um exemplo simples: Encontrar o maior elemento de um array.
Contando instruções
Neste artigo, vou utilizar várias linguagens de programação para os exemplos. Entretanto, não se desespere se você não conhecer uma linguagem de programação em específico. Como você já sabe programar, você deve ser capaz de ler os exemplos sem problema algum, mesmo se você não for familiar com a linguagem de programação escolhida, pois eles serão simples e não usarão nenhuma feature esotérica das linguagens. Se você for um estudante participando de competições de algoritmos, provavelmente você vai usar C++, então você não deverá ter problemas em acompanhar. Nesse caso, eu recomendo trabalhar nos exercícios usando C++ para praticar.
O maior elemento de um array pode ser encontrado usando com um trecho de código simples como esse, escrito em Javascript. Dado uma array de entrada A de tamanho n:
var M = A[ 0 ];
for ( var i = 0; i < n; ++i ) {
if ( A[ i ] >= M ) {
M = A[ i ];
}
}
Agora, a primeira coisa que vamos fazer é contar quantas instruções fundamentais este código executa. Nós vamos fazer isso somente agora e isso não vai ser mais necessário à medida que desenvolvemos nossa teoria, então seja um pouquinho paciente enquanto fazemos isso. Ao analisarmos esse trecho de código, nós queremos quebrá-lo em instruções simples; coisas que podem ser executadas diretamente pela CPU — ou algo próximo disso. Nós vamos assumir que o nosso processador pode executar as seguintes operações precisando de apenas uma única instrução para cada uma:
- Atribuir um valor a uma variável
- Encontrar o valor de um elemento específico de um array
- Comparar dois valores
- Incrementar um valor
- Operações aritméticas básicas, como adição e multiplicação
Nós iremos assumir que ramificações(escolhas de partes do código entre if e else depois que a condição já tiver sido avaliada) ocorre instantaneamente e não iremos contar essas instruções. No código acima, a primeira linha do código é:
var M = A[ 0 ];
Isso requer duas instruções: Uma para acessar A[ 0 ] e uma para atribuir o valor para M (nós estamos assumindo que n é sempre pelo menos 1). Essas duas instruções são sempre requeridas pelo algoritmo, independente do valor de n. O código de inicialização do loop for também tem que ser executado sempre. Isso nos dá mais duas instruções: uma atribuição e uma comparação:
i = 0;
i < n;
Elas vão ser executadas antes da primeira iteração do loop for Depois de cada iteração, nós vamos ter mais duas instruções para executar, um incremento de i e uma comparação para checar se vamos continuar no loop:
++i;
i < n;
Então, se ignorarmos o corpo do loop, o número de instruções que esse algoritmo precisa é 4 + 2n. Isso é, 4 instruções no começo do loop for e 2 instruções no final de cada iteração que nós temos em n. Nós podemos então definir uma função matemática f(n) que, dado um n, nos dá o número de instruções que o algoritmo precisa. Por exemplo, para um for com corpo vazio, nós temos f(n) = 4 + 2n.
Análise do pior caso
Agora, olhando para o corpo do for nós temos uma operação de acesso a um array e uma comparação, que sempre acontecem:
if ( A[ i ] >= M ) { ...
Aqui são duas instruções. Mas o corpo do if pode ou não pode ou não ser executado, dependendo de quais são os valores do array. Se A[ i ] >= M, então nós vamos executar essas duas instruções adicionais - um acesso ao array e uma atribuição:
M = A[ i ]
Mas agora, não podemos definir um f(n) tão facilmente, porque o número de instruções não depende somente de n mas também da entrada. Por exemplo, se A = [ 1, 2, 3, 4 ], o algoritmo vai precisar de mais instruções do que se A = [ 4, 3, 2, 1 ]. Quando analisamos algoritmos, nós geralmente consideramos o pior caso. Qual a pior coisa que pode acontecer para o nosso algoritmo? Quando o nosso algoritmo precisa do maior número possível de instruções para ser concluído? Nesse caso, é quando nós temos um array em ordem crescente, como A = [ 1, 2, 3, 4 ]. Então, M precisa ser substituído em cada iteração, de forma que teremos o maior número de instruções. Cientistas da computação têm um nome chique pra isso e o chamam de análise do pior caso; E isso não é nada mais do que simplesmente considerar o caso em que temos a pior sorte possível. Então, no pior caso, nós temos 4 instruções para executar dentro do corpo do for , então nós temos que f(n) = 4 + 2n + 4n = 6n + 4. Esta função f, dado um problema de tamanho n, nos dá o número de instruções que precisaríamos executar no pior caso.
Comportamento assintótico
Dada uma função dessa forma, nós temos uma boa ideia do quão rápido é um algoritmo. Entretanto, como eu prometi, nós não vamos precisar passar pela tarefa tediosa de contar instruções no nosso programa. Além disso, o número real de instruções que a CPU precisa executar para cada linguagem de programação depende do compilador da linguagem e do conjunto de instruções disponível (por exemplo, se o processador é um AMD ou um Intel Pentium no seu PC, ou um processador MIPS no seu Playstation 2) e nós dissemos que vamos ignorar isso. Agora, vamos passar nossa "função f" por um "filtro" que vai nos ajudar a eliminar esses pequenos detalhes que cientistas da computação preferem ignorar.
Na nossa função, 6n + 4, nós temos dois termos: 6n e 4. Na análise de complexidade nós apenas nos importamos com o que acontece na função de contagem de instruções quando a entrada do programa (n) fica muito grande. Isso combina bem com as ideias anteriores de comportamento no "pior caso": Nós estamos interessados em como o nosso algoritmo se comporta quando é exigido bastante dele; quando ele é desafiado a fazer algo realmente difícil. Note que isso é muito útil quando comparamos algoritmos. Se um algoritmo ganha de outro para uma entrada muito grande, então provavelmente o algoritmo mais rápido vai permanecer mais rápido quando for dado a ele uma entrada menor e mais fácil. Dos termos que estamos considerando, nós descartamos todos os termos que crescem lentamente e conservamos apenas aqueles que crescem depressa a medida que n se torna maior. Claramente 4 permanece 4 a medida que n vai crescendo, mas 6n fica cada vez maior e maior, então ele tende a importar mais para problemas maiores. Logo, a primeira coisa que nós vamos fazer é descartar o 4 e manter a função como f( n ) = 6n.
Isso faz sentido se você pensar um pouco a respeito, pois 4 é simplesmente uma "constante de inicialização". Diferentes linguagens de programação podem precisar de intervalos de tempo diferentes para se prepararem. Por exemplo, Java precisa de algum tempo para inicializar a sua máquina virtual. Como estamos ignorando as diferenças entre as linguagens de programação, faz todo o sentido ignorarmos esse valor.
A segunda coisa que vamos ignorar é a constante multiplicativa na frente do n, então nossa função vai se tornar f( n ) = n. Como você pode ver, isso simplifica bastante as coisas. Novamente, faz sentido descartar essa constante multiplicativa se nós pensarmos sobre como diferentes linguagens de programação se compilam. A "instrução" de acesso a um array pode se compilar para diferentes instruções em diferentes linguagens de programação. Por exemplo, em C, fazer A[ i ] não inclui uma verificação que checa se i está dentro do tamanho declarado para o array, enquanto que em Pascal isso está incluído. Então, o seguinte código em Pascal:
M := A[ i ]
É equivalente ao seguinde código em C:
if ( i >= 0 && i < n ) {
M = A[ i ];
}
Então, é razoável esperar que diferentes linguagens de programação vão nos dar diferentes fatores quando contamos suas instruções. No nosso exemplo, em que estamos usando um compilador burro de Pascal em que possíveis otimizações são óbvias, Pascal precisa de 3 instruções para cada acesso de array ao invés de 1 instrução necessária para o C. Descartar esse fator combina com ignorar as diferenças entre linguagens de programação e compiladores e somente analisar a ideia do algoritmo em si.
Esse filtro de "descartar todos os fatores" e de "manter o termo que mais cresce" como descrito acima é o que chamamos de comportamento assintótico. Então, o comportamento assintótico de f( n ) = 2n + 8 é descrito pela função f( n ) = n. Matematicamente falando, o que estamos falando aqui é que estamos interessados no limite da função f, onde n tende ao infinito; mas se você não entende o que essa frase significa formalmente, não se preocupe, porque isso é tudo o que você precisa saber. (Obs: Tecnicamente, se formos ser rigorosos, nós não podemos descartar as constantes no limite; mas na ciência da computação, nós queremos fazer isso pelas razões descritas acima.) Vamos fazer alguns exemplos para nos familiarizarmos com o conceito.
Vamos encontrar o comportamento assintótico para as seguintes funções de exemplo descartando fatores constantes e conservando os termos que crescem mais rápido.
f( n ) = 5n + 12 dá f( n ) = n.
Pelas mesmas razões escritas acima.
f( n ) = 109 dá f( n ) = 1.
Nós estamos descartando o multiplicador 109 * 1, mas ainda temos que colocar o 1 ali para indicar que a função possui um valor diferente de zero.
f( n ) = n2 + 3n + 112 dá f( n ) = n2
Aqui, n2 cresce mais do que 3n se n for grande o suficiente, então vamos mantê-lo.
f( n ) = n3 + 1999n + 1337 dá f( n ) = n3
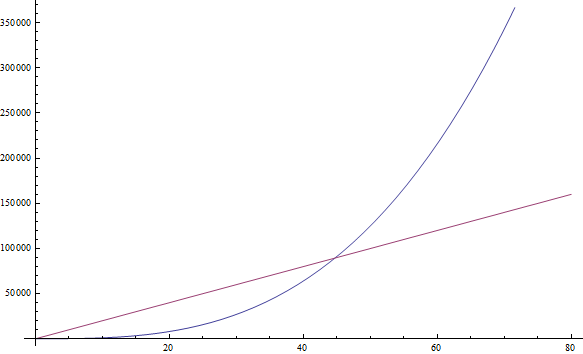
Mesmo que o fator na frente seja muito grande, nós ainda podemos encontrar um n grande o suficiente para que n3 seja maior que 1999n. Como estamos interessados no comportamento para valores muito grandes de n, nós conservamos apenas o3 (Veja a Figura 2).
f( n ) = n +
 dá f( n ) = n
dá f( n ) = nIsso acontece porque n aumenta mais rápido que
 a medida que n aumenta.
a medida que n aumenta.
Você também pode tentar os seguintes exemplos sozinho(a):
Exercicio 1
- f( n ) = n6 + 3n
- f( n ) = 2n + 12
- f( n ) = 3n + 2n
- f( n ) = nn + n
(Anote os seus resultados; a solução será dada abaixo)
Se você estiver tendo dificuldade com algum desses, coloque algum n muito grande e veja qual termo fica maior. Simples, né?
Complexidade
Então, o que isso diz pra gente, é que como podemos descartar todas essas constantes decorativas, é bem fácil dizer o comportamento assintótico de uma função de contagem de instruções de um programa. Na verdade, qualquer programa que não tem nenhum loop vai ter f( n ) = 1, uma vez que o número de instruções que ele precisa é uma constante(a não ser que ele use recursividade; veja abaixo). Qualquer programa com um único loop que vai de 1 a n vai ter f( n ) = n, uma vez que ele vai executar um número constante de instruções antes do loop, um número constante de instruções depois do loop, e um número constante de instruções dentro do loop que vão ser executadas todas as n vezes.
Isso deve ser bem mais fácil e menos chato do que contar instruções individuais, então vamos dar uma olhada em alguns exemplos para nos familiarizarmos com isso. O seguinte programa em PHP checa se um valor específico existe em um array A de tamanho n:
<?php
$exists = false;
for ( $i = 0; $i < n; ++$i ) {
if ( $A[ $i ] == $value ) {
$exists = true;
break;
}
}
?>
Este método de procurar um valor em um array é chamado de busca linear. Este é um nome razoável, porque esse programa é f( n ) = n (nós vamos definir exatamente o que "linear" significa na próxima seção). Você pode notar que tem uma instrução "break" ali que faz com que o programa termine mais cedo, mesmo depois de uma única iteração. Mas lembre-se de que estamos interessados no pior caso, que para esse programa é quando o array A não contém o valor. Então, ainda temos f( n ) = n.
Exercício 2
Analise sistematicamente a quantidade de instruções que o programa PHP acima precisa em respeito de n no pior caso para encontrar f( n ), de maneira similar a como analisamos nosso primeiro programa em Javascript. Então verifique que, assintoticamente, nós temos f( n ) = n.
Vamos olhar um programa em Python que soma dois elementos de um array juntos para produzir uma soma que é armazenada em outra variável:
v = a[ 0 ] + a[ 1 ]
Aqui nós temos um número constante de instruções, então temos que f(n) = 1.
O seguinte programa em C++ checa se um vector(um array mais chique) chamado A de tamanho n contém algum valor duplicado:
bool duplicate = false;
for ( int i = 0; i < n; ++i ) {
for ( int j = 0; j < n; ++j ) {
if ( i != j && A[ i ] == A[ j ] ) {
duplicate = true;
break;
}
}
if ( duplicate ) {
break;
}
}
Como aqui temos um loop aninhado dentro de outro, nós teremos um comportamento assintótico descrito por f( n ) = n2.
Regra geral: Programas simples podem ser analisados contando a quantidade de loops aninhados que eles possuem. Um único loop em n items nos dá f( n ) = n. Um loop dentro de outro loop nos dá f( n ) = n2. Um loop dentro de outro loop dentro de outro loop nos dá f( n ) = n3.
Se nós temos um programa que chama uma função dentro de um loop e nós sabemos o número de instruções dessa função, é fácil determinar o número de instruções de todo o programa. Vamos dar uma olhada nesse exemplo em C:
int i;
for ( i = 0; i < n; ++i ) {
f( n );
}
Se nós sabemos que f( n ) é uma função que executa exatamente n instruções, nós então sabemos que o número de instruções de todo o programa é assintoticamente n2, porque a função é chamada exatamente n vezes.
Regra geral: Dada uma série de loops que são sequenciais, o mais lento dentre eles determina o comportamento assintótico do programa. Dois loops aninhados seguidos de um único loop é assintoticamente o mesmo que somente os loops aninhados, porque os loops aninhados "dominam" o loop à parte.
Agora, vamos mudar para a notação chique que os cientistas da computação usam. Quando nós encontramos qual o valor assintótico exato de f, nós dizemos que nosso programa é Θ( f( n ) ). Por exemplo, os programas acima são Θ( 1 ), Θ( n2 ) e Θ( n2 ) respectivamente. Θ( n ) é pronunciado como "teta de n". As vezes dizemos que f( n ), a função original de contagem de instruções incluindo as constantes, é Θ( alguma coisa). Por exemplo, podemos dizer que f( n ) = 2n é uma função que é Θ( n ) — nada de novo aqui. Nós também podemos escrever 2n ∈ Θ( n ), que é pronunciado como "dois n pertence a teta de n". Não se confunda com essa notação: tudo o que ela diz é que se nós contarmos o número de instruções que um programa precisa e ele for 2n, então o comportamento assintótico do nosso algoritmo é descrito por n, que encontramos ao eliminar as constantes. Dada essa notação, a seguir temos algumas expressões matemáticas verdadeiras:
- n6 + 3n ∈ Θ( n6 )
- 2n + 12 ∈ Θ( 2n )
- 3n + 2n ∈ Θ( 3n )
- nn + n ∈ Θ( nn )
A propósito, se você resolveu o exercício 1 acima, essas são as respostas que você deveria encontrar.
Nós chamamos essa função, i.e. o que nós colocamos dentro Θ( daqui ), de complexidade de tempo, ou apenas complexidade do nosso algoritmo. Então um algoritmo Θ( n ) é de complexidade n. Nós também temos nomes especiais para Θ( 1 ), Θ( n ), Θ( n2 ) e Θ( log( n ) ) porque eles ocorrem com frequência. Nós dizemos que um algoritmo Θ( 1 ) é um algoritmo de tempo constante, Θ( n ) é linear, Θ( n2 ) é quadrático e Θ( log( n ) ) é logarítmico (não se preocupe se você ainda não sabe o que são logaritmos — nós vamos chegar lá daqui a pouco).
Regra geral:: Programas com um Θ maior são mais lentos que programas com um Θ menor.

Notação Big-O
Algumas vezes vai ser difícil descobrir exatamente qual o comportamento de um algoritmo da maneira que fizemos acima, especialmente para exemplos mais complexos. Entretanto, nós podemos dizer que o comportamento do nosso algoritmo nunca vai exceder um certo limite. Isso torna a nossa vida mais fácil, pois não vamos ter que especificar exatamente o quão rápido o nosso algoritmo roda, mesmo ignorando constantes como fizemos acima. Tudo que precisamos fazer é encontrar um certo limite. Isso é facilmente explicado com um exemplo.
Um problema bastante usado por cientistas para ensinar algoritmos é o problema de ordenação. No problema de ordenação, um array A de tamanho n é dado (parece familiar?) e temos que escrever um programa que ordena esse array. Esse problema é interessante porque é um problema pragmático em sistemas reais. Por exemplo, um explorador de arquivos precisa ordenar os arquivos que ele exibe por nome para facilitar a navegação do usuário. Ou, como outro exemplo, um video game pode precisar ordenar os objetos 3D exibidos no mundo com base em suas distâncias ao olho do jogador dentro do mundo virtual para determinar o que está visível e o que não está, algo chamado de Problema da visibilidade (veja a Figura 3). Os objetos mais próximos ao jogador são os visíveis, enquanto que aqueles que estão mais afastados podem estar escondidos atrás de outros objetos na frente deles. O problema de ordenação também é interessante porque existem muitos algoritmos algoritmos que o resolvem, alguns pior do que outros. Também é um problema fácil de se definir e explicar. Então, vamos escrever um trecho de código que ordena um array.
Eis aqui uma maneira ineficiente de se implementar uma ordenação em um array em Ruby. (Claro, Ruby permite a ordenação de arrays usando funções já inclusas na linguagem, que você deve utilizar, e que certamente serão mais rápidas do que o algoritmo que veremos aqui. Mas vamos criar um mesmo assim para ilustrar.)
b = []
n.times do
m = a[ 0 ]
mi = 0
a.each_with_index do |element, i|
if element < m
m = element
mi = i
end
end
a.delete_at( mi )
b << m
end
Esse método é conhecido como selection sort. Ele encontra o menor elemento do nosso array (o array está denotado como a acima, enquanto que o menor valor é denotado como m e mi é o seu índice), o coloca em um novo array (no caso, b), e o remove do array original. Então ele encontra o mínimo entre os valores restantes do array original e o coloca no fim do novo array de modo que agora ele vai conter dois elementos, e o remove do array original. O processo continua até que todos os items tenham sido removidos do array original e inseridos no novo array, o que significa que o novo array estará ordenado. Nesse exemplo, nós podemos ver que temos dois loops aninhados. O loop externo é executado n vezes, e o loop interno é executado uma vez para cada elemento do array a. O array a inicialmente tem n itens, mas nós estamos removendo um item a cada iteração. Então o loop interno se repete n vezes durante a primeira iteração do loop externo, depois n - 1 vezes, depois n - 2 vezes, e assim por diante, até a última iteração do loop externo, onde vai ser executado somente uma vez.
É meio difícil avaliar a complexidade desse programa, pois teríamos que dar um jeito de somar 1 + 2 + … + (n - 1) + n. Mas nós podemos encontrar um "limite superior" para ele. Isso é, podemos alterar o nosso programa (você pode fazer isso na sua cabeça, não no código ) para o tornar pior do que ele é e então encontrar a complexidade do novo programa criado a partir dele. Se nós encontrarmos a complexidade do programa pior que nós fizemos, então vamos saber que o nosso programa original vai ser no máximo tão ruim quanto, ou talvez será até melhor do que ele. Dessa forma, se encontrarmos uma complexidade muito boa para o programa alterado, que é pior que o original, nós vamos saber que o nosso programa original também vai ter uma complexidade muito boa — tão boa quanto o nosso programa alterado, ou até melhor.
Vamos agora pensar em uma maneira de modificar esse programa exemplo para o tornar mais fácil de se descobrir sua complexidade. Mas tenha em mente que nós só o podemos torná-lo pior, por exemplo, criando mais instruções, para que a nossa estimativa seja significativa para o programa original. Claramente nós podemos alterar o loop interno do programa para sempre se repetir exatamente n vezes, ao invés de um número variável de vezes. Algumas dessas repetições vão ser inúteis, mas vão nos ajudar a analisar a complexidade do algoritmo resultante. Se nós fizermos essa simples mudança, então o novo algoritmo que construímos é claramente Θ( n2 ), porque nós temos dois loops aninhados que se repetem exatamente n vezes. Se é assim, podemos dizer que o algoritmo original é O( n2 ). O( n2 ) é pronunciado como "O de n ao quadrado". O que isso diz é que o nosso programa não é assintoticamente pior do que n2. Pode ser até melhor do que isso, ou talvez seja a mesma coisa. A propósito, se o programa realmente for Θ( n2 ), nós ainda podemos dizer que ele é O( n2 ). Para ajudar na compreensão, imagine o programa sendo alterado de uma maneira que não o mude muito, mas o faz um pouquinho pior, como adicionando uma instrução sem importância no começo do programa. Fazer isso vai alterar a função contadora de instruções com uma simples constante, que é ignorada quando analisamos seu comportamento assintótico. Então um programa que é Θ( n2 ) também é O( n2 ).
Mas um programa que é O( n2 ) pode não ser Θ( n2 ). Por exemplo, qualquer programa que é Θ( n ) também é O( n2 ) além de ser O( n ). Se imaginarmos que um programa Θ( n ) é um simples loop for que se repete n vezes, nós podemos torná-lo pior o colocando dentro de outro loop for que também se repete n vezes, produzindo assim um programa f( n ) = n2. Para generalizar, qualquer programa que for Θ( a ) também é O( b ) se b for pior que a. Note que a nossa alteração ao programa não precisa gerar um programa que seja significativo ou equivalente ao programa original. Ele só precisa executar mais instruções que o programa original para um dado n. Tudo que estamos usando é para contar instruções, e não para resolver o problema em si.
Então, dizer o que nosso programa é O( n2 ) é ficar na zona de conforto: Nós analisamos o nosso algoritmo, e descobrimos que ele nunca vai ser pior que n2. Mas pode ser mesmo que ele seja n2. Isso nos dá uma boa estimativa do quão rápido nosso programa é executado. Vamos olhar alguns exemplos para ajudar com a familiarização dessa nova notação.
Exercise 3
Descubra quais afirmações são verdadeiras:
- Um algoritmo Θ( n ) é O( n )
- Um algoritmo Θ( n ) é O( n2 )
- Um algoritmo Θ( n2 ) é O( n3 )
- Um algoritmo Θ( n ) é O( 1 )
- Um algoritmo O( 1 ) é Θ( 1 )
- Um algoritmo O( n ) é Θ( 1 )
Solução
- Sabemos que essa é verdadeira porque nosso programa original era Θ( n ). Nós podemos chegar em O( n ) sem alterar absolutamente nada no nosso programa.
- Como n2 é pior que n, essa é verdadeira.
- Como n3 é pior que n2, essa é verdadeira.
- Como 1 não é pior que n, essa é falsa. Se um programa precisa de n instruções assintoticamente (uma quantidade linear de instruções), nós não podemos torná-lo pior e fazer com que ele tenha apenas 1 instrução assintoticamente (uma quantidade constante de instruções)
- Essa é verdadeira porque as duas complexidades são iguais.
- Essa pode ou não ser verdadeira dependendo do algoritmo. Em um caso geral, é falsa. Se um algoritmo é Θ( 1 ), então ele certamente é O( n ). Mas se ele for O ( n ) então ele pode não ser Θ( 1 ). Por exemplo, um algoritmo Θ( n ) é O ( n ) mas não é Θ( 1 ).
Exercício 4
Use uma progressão aritmética para provar que o programa acima não só é O( n2 ) como também é Θ( n2 ). Se você não souber o que é uma progressão aritmética, olhe na Wikipedia – é fácil.
Como a complexidade O de um algoritmo nos dá o limite superior para a complexidade real dele enquanto que Θ nos dá a complexidade exata do algoritmo, as vezes dizemos que Θ nos dá um limite estreito. Se sabemos que encontramos um limite de complexidade que não é estreito, nós podemos usar um "o" minúsculo para denotar isso. Por exemplo, se um algoritmo é Θ( n ), então sua complexidade estreita é n. Então esse algoritmo é tanto O( n ) quanto O( n2 ). Como o algoritmo é Θ( n ), o limite O( n ) é um limite estreito. Mas o limite O( n2 ) não é estreito, então nós podemos escrever que o algoritmo é o( n2 ), para ilustrar que nós sabemos que o limite não é estreito. Essa notação também é conhecida como notação "little o". É melhor se nós pudermos encontrar os limites estreitos dos nossos algoritmos, porque eles nos dão mais informação sobre como nosso algoritmo se comporta, mas isso nem sempre é fácil de se fazer.
Exercício 5
Determine quais dos seguintes limites são estreitos e quais não são. Verifique se existe algum limite pode estar errado. Use a notação little o para ilustrar os limites que não são estreitos.
- Um algoritmo Θ( n ) para o qual encontramos um limite superior O( n ).
- Um algoritmo Θ( n2 ) Para qual encontramos um limite superior O( n3 ),
- Um algoritmo Θ( 1 ) para qual encontramos um limite superior O( n ).
- Um algoritmo Θ( n ) para qual encontramos um limite superior O( 1 ).
- Um algoritmo Θ( n ) para qual encontramos um limite superior O( 2n ).
Solution
- Nesse caso, a complexidade Θ e a complexidade O são as mesmas, então o limite é estreito.
- Aqui vemos que a complexidade O é de uma escala maior do que a complexidade Θ, então esse limite não é estreito. Para ser estreito, o limite deveria ser de O( n2 ). Então nós podemos escrever que o algoritmo é o( n3 ).
- Novamente vemos que a complexidade O é de uma escala maior que a complexidade Θ, então temos um limite que não é estreito. Um limite de O( 1 ) seria estreito. Então podemos indicar que o limite O( n ) não é estreito o escrevendo como o( n ).
- Devemos ter cometido algum erro no cálculo desse limite, porque está errado. É impossível para um algoritmo Θ( n ) ter um limite superior de O( 1 ), pois n é uma complexidade maior do que 1. Lembre-se que O dá o limite superior.
- Esse pode parecer um limite que não é estreito, mas isso não é verdade. Esse limite é de fato estreito. Lembre-se que o comportamento assintótico de 2n é n são os mesmos, e que para as notações O e Θ importam apenas os comportamentos assintóticos. Então nós temos que O( 2n ) = O( n ) e então esse limite é estreito, pois sua complexidade é a mesma de Θ.
Rergra geral: É mais fácil descobrir a complexidade O de um algoritmo do que a sua complexidade Θ.
Você pode estar ficando um pouco confuso com todas essas novas notações, mas vou apresentar só mais dois símbolos antes de irmos para alguns exemplos. Eles vão ser fáceis agora que você já conhece Θ, O e o, e nós não vamos usá-los muito daqui pra frente, mas é bom aproveitar a oportunidade para conhecê-los. No exemplo acima, nós modificamos o programa para torná-lo pior (executando mais instruções, o que aumenta o tempo de execução) e introduzimos a notação O. A notação O é importante porque nos diz informações valiosas para sabermos se o programa é bom o suficiente. Se fizermos o oposto e modificarmos nosso programa para torná-lo melhor encontrarmos a complexidade do programa resultante, nós usamos a notação Ω. Ω então nos dá uma complexidade que nós sabemos que o nosso programa não vai ser melhor que ela. Isso é útil se quisermos provar que um programa roda mais lentamente ou que um algoritmo é ruim. Também pode ser usado para argumentar que um algoritmo é muito lento para ser usado em algum caso específico. Por exemplo, dizer que um algoritmo é Ω( n3 ) significa que o algoritmo não é melhor que n3. Ele pode ser Θ( n3 ), tão ruim quanto Θ( n4 ) ou até pior, mas sabemos que é pelo menos tão ruim quanto n3. Então Ω nos dá um limite inferior para a complexidade do nosso algoritmo. De maneira similar ao "o", nós podemos escrever ω se soubermos que nosso limite não é estreito. Por exemplo, um algoritmo Θ( n3 ) é ο( n4 ) e ω( n2 ). Ω( n ) se pronuncia como "grande omega de n" enquanto que ω( n ) se pronuncia "pequeno omega de n"
Exercício 6
Para as seguintes complexidades Θ, escreva um limite O estreito e um não estreito, além de um limite Ω estreito outro não estreito de sua escolha, desde que eles existam.
- Θ( 1 )
- Θ(
 )
) - Θ( n )
- Θ( n2 )
- Θ( n3 )
Solução
Essa é uma aplicação intuitiva dos concentos que vimos acima.
- Os limites estreitos vão ser O( 1 ) e Ω( 1 ). Um limite O não estreito seria O( n ). Lembre-se que O nos dá um limite superior. Como n é de uma escala maior que 1, esse limite não é estreito, então também podemos escrevê-lo como o( n ). Mas não é possível encontrar um limite não estreito para Ω, pois não podemos usar um valor menor que 1 para essas funções. Então vamos ter que usar somente o limite estreito.
- Os limites estreitos vão ter que ser os mesmos da complexidade Θ, então eles são O(
 ) e Ω(
) e Ω(  ) respectivamente. Para limite superior não estreito, nós podemos usar O( n ), porque n é maior que
) respectivamente. Para limite superior não estreito, nós podemos usar O( n ), porque n é maior que  então é um limite superior para
então é um limite superior para  . Como sabemos que ele é um limite não estreito, também podemos escrevê-lo como o( n ). Para um limite inferior não estreito, podemos simplesmente utilizar Ω( 1 ). Como sabemos que esse limite não é estreito, também podemos escrevê-lo como ω( 1 ).
. Como sabemos que ele é um limite não estreito, também podemos escrevê-lo como o( n ). Para um limite inferior não estreito, podemos simplesmente utilizar Ω( 1 ). Como sabemos que esse limite não é estreito, também podemos escrevê-lo como ω( 1 ). - Os limites estreitos são O( n ) e Ω( n ). Dois limites não estreitos podem ser ω( 1 ) e o( n3 ). Esses na verdade são limites bem ruins, porque estão longe das complexidades originais, mas ainda são válidos de acordo com as nossas definições.
- Os limites estreitos são O( n2 ) e Ω( n2 ). Para limites não estreitos podemos novamente usar ω( 1 ) e o( n3 ) assim como no exemplo anterior.
- Os limites estreitos são O( n3 ) e Ω( n3 ) respectivamente. Dois limites não estreitos podem ser ω(
 n2 ) e o(
n2 ) e o(  n3 ). Mesmo sendo limites não estreitos, eles ainda são melhores que os que demos acima.
n3 ). Mesmo sendo limites não estreitos, eles ainda são melhores que os que demos acima.
A razão de usarmos O e Ω ao invés de Θ mesmo que O e Ω possam dar intervalos estreitos é que pode ser que não sejamos capazes de determinar se um intervalo que encontramos é realmente estreito, ou talvez só não queremos passar pelo processo verificá-lo cuidadosamente.
Se você não entender muito bem todos os símbolos diferentes e seus usos, não se preocupe muito com isso agora. Você pode sempre voltar e dar outra olhada. Os símbolos mais importantes são O e Θ.
Note também que mesmo Ω nos dando um limite inferior para a nossa função (ou seja, melhoramos o programa e agora ele executa menos instruções) nós ainda estamos nos referindo a análise do pior caso. Isso acontece porque nós estamos alimentando o nosso programa com a pior entrada possível para um dado n e analisando o seu comportamento a partir desse princípio.
A tabela seguinte mostra os símbolos que acabamos de apresentar e sua correspondência com os símbolos matemáticos que geralmente usamos com números. A razão para não usarmos os símbolos matemáticos aqui e usarmos letras gregas é para indicar que estamos realizando uma comparação entre comportamentos assintóticos, e não somente simples comparações.
| Operador de comparação assintótica | Operador de comparação numérica |
|---|---|
| Nosso algoritmo é o( alguma coisa ) | Um número é < alguma coisa |
| Nosso algoritmo é O( alguma coisa ) | Um número é ≤ something |
| Nosso algoritmo é Θ( alguma coisa ) | Um número é = alguma coisa |
| Nosso algoritmo é Ω( alguma coisa ) | Um número é ≥ alguma coisa |
| Nosso algoritmo é ω( alguma coisa ) | Um número é > alguma coisa |
Regra geral: Mesmo que todos os símbolos O, o, Ω, ω e Θ sejam úteis, O é o que é mais utilizado, porque é mais fácil de se determinar do que Θ e tem mais utilidade prática do que Ω.
Logarítmos
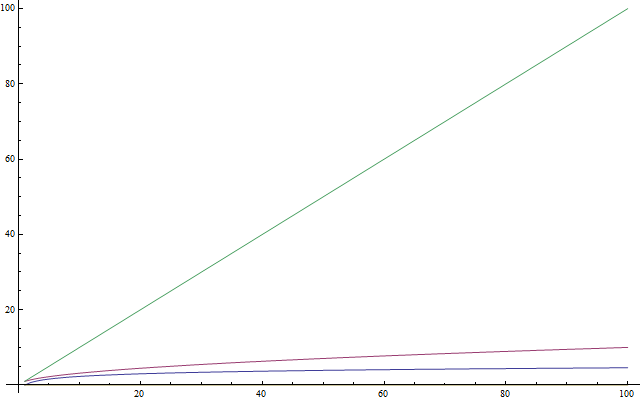
Se você já sabe o que são logaritmos, sinta-se livre para pular essa seção. Como muita gente não os conhece, ou simplesmente não o usaram tanto ultimamente e não se lembram bem deles, essa seção é uma introdução. Esse texto também é para estudantes mais jovens que ainda não estudaram logaritmos na escola. Logaritmos são importantes porque eles aparecem bastante quando analisamos complexidade. Um logaritmo é uma operação aplicada a um número que o torna bem menor - como uma raiz quadrada de um número. Então se tem uma coisa que você vai querer lembrar de logaritmos, é que eles pegam um número e o tornam bem menor que o número original (Veja a Figura 4). Agora, da mesma maneira que a raiz quadrada é a operação inversa de elevar alguma coisa ao quadrado, o logaritmo é a operação inversa da exponenciação. Não é tão difícil quanto parece. Fica melhor explicado com um exemplo. Considere essa equação:
2x = 1024
Nós queremos resolver essa equação para x. Então nos perguntamos: Qual é a potência de base 2 que é igual a 1024? Esse número é o 10. Então, nós temos que 210 = 1024, o que é fácil de se verificar. Logaritmos nos ajudam a representar esse problema com uma nova notação. Nesse caso, 10 é o logaritmo de 1024 e nós o escrevemos como log ( 1024 ) e o lemos como "o logaritmo de 1024". Como estamos usando o 2 como base, nós o chamamos de logaritmo de base 2. Existem logaritmos e outras bases, mas vamos usar somente logaritmos de base 2 nesse artigo. Se você é um estudante que participa de competições internacionais e não sabe logaritmos, eu recomendo fortemente que você os pratique depois de terminar de ler esse artigo. Na ciência da computação, logaritmos de base 2 são muito mais comuns que qualquer outro tipo de logaritmo. Isso acontece porque geralmente temos somente duas entidades diferentes: 0 e 1. Nós também tendemos a dividir problemas grandes em metades, que são sempre duas. Então você só precisa saber logaritmos de base 2 para continuar nesse artigo.
Exercício 7
Resolva as equações abaixo. Escreva o logaritmo que você encontrar em cada caso. Use somente logaritmos de base 2.
- 2x = 64
- (22)x = 64
- 4x = 4
- 2x = 1
- 2x + 2x = 32
- (2x) * (2x) = 64
Solução
Não é preciso fazer mais nada além de aplicar as ideias definidas acima.
- Por tentativa e erro podemos encontrar que x = 6, e então log( 64 ) = 6.
- Aqui podemos notar que (22)x, pelas propriedades da exponenciação, pode ser escrito como 22x. Então temos que 2x = 6 porque log( 64 ) = 6 de acordo com o exercício anterior, portanto x = 3.
- Usando o que sabemos da equação anterior, podemos escrever 4 como 22 então nossa equação se torna (22)x = 4 que é o mesmo que 22x = 4. Então notamos que log( 4 ) = 2 porque 22 = 4 então temos que 2x = 2, logo x = 1. Isso é facilmente observado a partir da equação original, uma vez que usar um exponente igual a 1 nos dá a base como resultado.
- Lembre-se que um expoente 0 nos dá 1 como resultado. Então temos que log( 1 ) = 0 pois 20 = 1, então x = 0.
- Aqui temos uma soma, então não podemos calcular o logaritmo diretamente. Porém, notamos que 2x + 2x é o mesmo que 2 * (2x). que por sua vez é igual a 2x + 1. Agora, tudo que temos que fazer é resolver a equação 2x + 1 = 32. Nós encontramos log( 32 ) = 5, então x + 1 = 5, resultando que x = 4.
- Nós estamos multiplicando duas potências de base 2, então podemos juntá-las notando que (2x) * (2x) é o mesmo que 22x. Então, tudo que temos que fazer é resolver a equação 22x = 64 que já resolvemos acima, então x = 3.
Regra geral: Para algoritmos de competições implementados em C++, depois que você analisa a complexidade, você pode fazer uma estimativa do quão rápido o seu programa irá executar assumindo que ele realiza cerca de 1.000.000 operações por segundo, onde a quantidade de operações que você contou são dadas pelo comportamento assintótico da função que descreve o seu algoritmo. Por exemplo, um algoritmo Θ( n ) leva cerca de um segundo para processar uma entrada n = 1.000.000.
Complexidade recursiva
Vamos agora dar uma olhada em uma função recursiva. Uma função recursiva é uma função que chama a ela mesma. Podemos analisar a complexidade dela? A seguinte função, escrita em Python, calcula o fatorial de um número. O fatorial é um número inteiro positivo que é encontrado ao se multiplicar esse número com todos os números inteiros positivos anteriores. Por exemplo, o fatorial de 5 é 5 * 4 * 3 * 2 * 1. Nós o denotamos como "5!" e o pronunciamos como "cinco fatorial" (algumas pessoas preferem pronunciar gritando como "CINCO!!!").
def factorial( n ):
if n == 1:
return 1
return n * factorial( n - 1 )
Vamos analisar a complexidade dessa função. Essa função não tem nenhum loop, mas sua complexidade não é constante. Para encontrarmos sua complexidade, temos novamente que contar as suas instruções. Claramente, se passarmos algum n para essa função, ele vai ser executada n vezes. Se você não tiver certeza disso, execute agora a função "na mão" para n = 5 para validar se ela realmente funciona. Por exemplo, para n = 5, ela será executada 5 vezes, porque ela vai decrementar n em 1 a cada chamada. Nós podemos então ver que essa função é Θ( n ).
Se você não tiver certeza disso, lembre-se que você pode sempre encontrar a complexidade exata ao contar as instruções. Se você quiser, pode tentar contar as instruções executadas por essa função e encontrar uma função f( n ) e verificar se ela é realmente linear (lembre-se que linear significa Θ( n )).
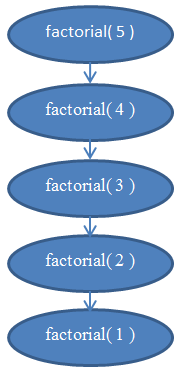
Veja a Figura 5 com um diagrama para lhe ajudar a entender as chamadas recursivas que são feitas quando a função factorial(5) é chamada.
Isso deve deixar claro o porquê dessa função ser linear.
Complexidade logaritmica
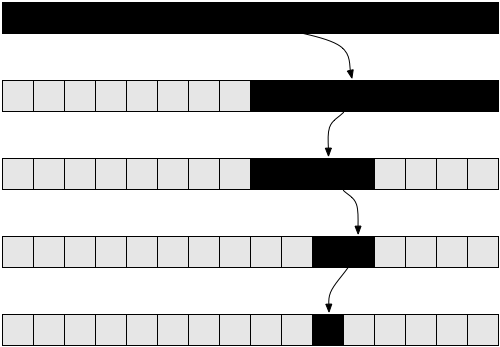
Um problema famoso na ciência da computação é o de encontrar um valor em um array. Nós resolvemos esse problema anteriormente para um caso geral. Esse problema se torna interessante se tivermos um array que está ordenado e queremos encontrar um certo valor dentro dele. Um maneira para se fazer isso é conhecida como busca binária. Nós olhamos o elemento do meio no nosso array: Se o encontrarmos ali, então terminamos. Caso contrário, se o valor que encontrarmos for menor que o valor pelo qual estamos procurando, nós sabemos que o elemento estará na parte esquerda do array. Caso contrário, nós sabemos que ele estará na parte direita do array. Nós podemos continuar cortando o array em partes menores até termos um único elemento para olhar. Eis o método usando pseudocódigo:
def binarySearch( A, n, value ):
if n = 1:
if A[ 0 ] = value:
return true
else:
return false
if value < A[ n / 2 ]:
return binarySearch( A[ 0...( n / 2 - 1 ) ], n / 2 - 1, value )
else if value > A[ n / 2 ]:
return binarySearch( A[ ( n / 2 + 1 )...n ], n / 2 - 1, value )
else:
return true
Esse pseudocódigo é uma simplificação da implementação verdadeira. Na prática, esse método é mais fácil descrito do que implementado, porque o(a) programador(a) precisa tomar cuidado com alguns detalhes na implementação. Podem existir erros em expressões booleanas e a divisão por 2 nem sempre vai resultar em um valor inteiro, então será necessário arredondar o valor com floor() ou ceil(). Mas podemos assumir para os nossos propósitos que ela vai sempre ser bem sucedida, e que a nossa implementação está livre desses erros, pois queremos apenas analisar a complexidade desse método. Se você nunca implementou uma busca binária antes, pode ser que você queria fazer isso na sua linguagem de programação favorita. É um esforço realmente esclarecedor.
Veja a Figura 6 para ajudar no entendimento de como a busca binária funciona.
Se você tiver dúvidas se esse método realmente funciona, aproveite agora para rodar ele na mão em um exemplo simples e convença a si mesmo que ele realmente funciona.
Vamos agora tentar analisar o algoritmo. Novamente, nós temos um algoritmo recursivo. Vamos assumir, para simplificar as coisas, que o array sempre será cortado exatamente no meio, ignorando a parte do +1 e -1 na chamada recursiva. Você já deve estar convencido de que uma pequena mudança como ignorar +1 e -1 não vai afetar o resultado da complexidade. Esse é um fato que normalmente teríamos que provar se quiséssemos ser prudentes de um ponto de vista matemático, mas na prática isso já é intuitivo. Vamos assumir que nosso array tem um tamanho que é uma potência de 2, também para simplificar. Novamente, isso não muda o resultado final da complexidade que vamos encontrar. O pior caso para esse problema é quando o valor pelo qual estamos procurando não existe no array. Nesse caso, começamos com um array de tamanho n na primeira chamada recursiva, então temos um array de tamanho n / 2 na próxima chamada. Então teremos um array de tamanho n / 4 na próxima chamada, seguido por um array de tamanho n / 8, e assim por diante. Em geral, nosso array é dividido pela metade em cada chamada, até encontrarmos um array de tamanho 1. Então, vamos escrever o número de elementos no nosso array para cada chamada:
Note que na i-ésima iteração, nosso array tem n / 2i elementos. Isso acontece porque a cada iteração nós estamos cortando nosso array pela metade, o que significa que estamos dividindo o seu número de elementos por 2. Isso se traduz em multiplicar o denominador por 2. Se fizermos isso i vezes, temos n / 2i. Esse procedimento continua e quanto maior for o i, menor vai ser a quantidade de elementos até chegarmos na última iteração em que teremos apenas um único elemento restante. Se quisermos encontrar o i para vermos em qual iteração isso acontece, temos que resolver a seguinte equação:
1 = n / 2i
Ela somente será verdadeira quando tivermos chegado na última chamada da função binarySearch(), e não em um caso geral. Então resolver a equação para i nos ajuda a encontrar em qual iteração a recursão vai terminar. Multiplicando ambos os lados por 2i nos dá:
2i = n
Esta equação deve parecer familiar se você leu a seção de logaritmos acima. Resolver essa equação para i nos dá:
i = log( n )
Isto nos diz que o número de iterações necessárias para realizar uma busca binária é log( n ), onde n é o número de elementos do array original.
Se você pensar sobre isso, vai ver que faz sentido. Por exemplo, seja n = 32, um array de 32 elementos. Quantas vezes teremos que cortá-lo pela metade para chegar em apenas 1 elemento? Nós temos 32 → 16 → 8 → 4 → 2 → 1. Fizemos isso 5 vezes, que é o logaritmo de 32. Logo, a complexidade da busca binária é Θ( log( n ) ).
Esse último resultado nos permite comparar a busca binária com a busca linear, nosso método anterior. Claramente, como log( n ) é muito menor que n, é razoável concluir que a busca binária é um método bem mais rápido de busca em um array do que a busca linear, então é recomendado sempre manter nossos arrays ordenados se quisermos fazer muitas buscas neles.
Regra geral: Melhorar o comportamento assintótico de um programa geralmente aumenta muito a sua performance, muito mais do que qualquer pequena otimização "técnica" como usar uma linguagem de programação mais rápida.
Ordenação ótima
Parabéns. Você sabe sobre análise de complexidade de algoritmos, comportamento assintótico de funções e a notação big-O. Você também sabe, de forma intuitiva, descobrir se a complexidade de um algoritmo é O( 1 ), O( log( n ) ), O( n ), O( n2 ) e assim por diante. Você conhece os símbolos o, O, ω, Ω e Θ, e sabe o que significa análise do pior caso. Se você chegou a esse ponto, esse tutorial já serviu o seu propósito.
Essa última seção é opcional. É um pouco mais aprofundada, então sinta-se livre para pulá-la se você sentir que é demais. Ela vai precisar do seu foco e que você gaste alguns momentos trabalhando nos exercícios. Entretanto, ela vai te dar um método muito útil na análise de complexidade de algoritmos que pode ser muito poderoso, então certamente vale a pena entender.
Nós vimos uma implementação de ordenação acima chamada selection sort. Nós mencionamos que o selection sort não é ótimo. Um algoritmo ótimo é um algoritmo que resolve um problema da melhor maneira possível, o que significa que não existe um algoritmo melhor pra isso. Isso quer dizer que todos os outros algoritmos para resolver esse problema tem uma complexidade igual ou pior que o algoritmo ótimo. Podem existir muitos algoritmos ótimos para um problema com todos eles compartilhando da mesma complexidade. O problema de ordenação pode ser resolvido de maneira ótima de várias formas. Nós podemos usar a mesma ideia da busca binária para ordenar rapidamente. Esse método de ordenação é chamado de mergesort.
Para fazer um mergesort, primeiro precisamos criar uma função auxiliar que vamos usar para fazer a ordenação de fato. Nós vamos criar uma função merge que pega dois arrays que já estão ordenados e os junta em um array maior ordenado. Isso é fácil:
def merge( A, B ):
if empty( A ):
return B
if empty( B ):
return A
if A[ 0 ] < B[ 0 ]:
return concat( A[ 0 ], merge( A[ 1...A_n ], B ) )
else:
return concat( B[ 0 ], merge( A, B[ 1...B_n ] ) )
A função concat pega um item, a "cabeça", e um array, a "cauda", e constrói e retorna um novo array que contém a "cabeça" como primeiro item no novo array e a "cauda" como o resto dos elementos do array. Por exemplo, concat(3, [4, 5, 6]) retorna [3, 4, 5, 6] . Nós usamos A_n e B_n para denotar os tamanhos dos arrays A e B, respectivamente.
Exercício 8
Verifique que a função acima realmente faz uma união de dois arrays. Reescreva-o em sua linguagem de programação favorita em uma forma iterativa (usando loops for) ao invés de recursão.
Analisar esse algoritmo revela que ele tem um tempo de execução de Θ( n ), onde n é o tamanho do array resultante (n = A_n + B_n).
Exercício 9
Verifique que o tempo de execução do merge é de Θ( n ).
Utilizando essa função, podemos construir um algoritmo de ordenação melhor. A ideia é a seguinte: Nós dividimos o array em duas partes. Então, ordenamos cada parte recursivamente, para em seguida unir os dois arrays ordenados em um array maior. Em pseudocódigo:
def mergeSort( A, n ):
if n = 1:
return A # já está ordenado
middle = floor( n / 2 )
leftHalf = A[ 1...middle ]
rightHalf = A[ ( middle + 1 )...n ]
return merge( mergeSort( leftHalf, middle ), mergeSort( rightHalf, n - middle ) )
Esta função é mais difícil de se entender do que a que vimos anteriormente, então o próximo exercício pode levar alguns minutos.
Exercício 10
Verifique se o mergeSort está correto. Isso é, cheque se o mergeSort como definido acima ordena corretamente o array que é dado a ele. Se você estiver tendo dificuldades para entender porque ele funciona, tente com um array de exemplo pequeno e rode ele "na mão". Quando executar essa função na mão, certifique-se que leftHalf e rightHalf são o que você consegue se cortar o array aproximadamente no meio; ele não tem que estar exatamente no meio se o array tiver um número ímpar de elementos (foi pra isso que usamos o floor acima).
Como exemplo final, vamos analisar a complexidade do mergeSort. Em cada passo do mergeSort, estamos dividindo o array em duas metades de tamanho igual, de maneira similar a binarySearch. Entretanto, nesse caso, nós vamos manter ambas as metades durante a execução. Então aplicamos o algoritmo recursivamente em cada metade. Depois que a recursão terminar, aplicamos a operação merge no resultado, o que leva um tempo Θ( n ).
Então, nós dividimos o array original em dois arrays de tamanho n / 2 cada. Em seguida nós unimos os dois arrays, em uma operação que une n elementos e que portanto, leva um tempo Θ( n ).
Dê uma olhada na Figura 7 para entender essa recursão.
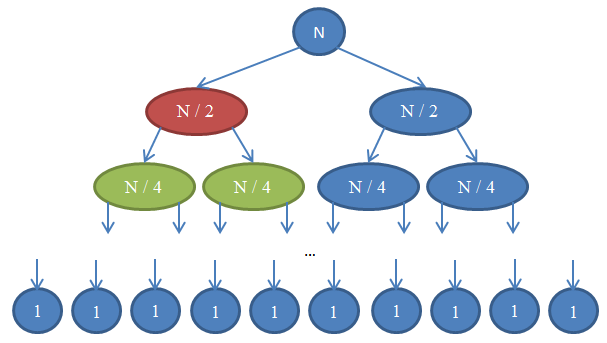
Vamos ver o que está acontecendo aqui. Cada círculo representa uma chamada à função mergeSort. O número escrito dentro do círculo mostra o tamanho do array que está sendo ordenado. O círculo azul no topo é a chamada inicial ao mergeSort, onde temos que ordenar um array de tamanho n. As flechas indicam chamadas recursivas feitas entre funções. A chamada inicial do mergeSort faz duas chamdas para mergeSort em dois arrays, cada um de tamanho n / 2. Isso é indicado pelas duas flechas no topo. Por sua vez, cada uma dessas chamadas faz mais duas outras chamadas para mergeSort em mais dois arrays, cada um de tamanho n / 4, e assim por diante até chegarmos nos arrays de tamanho 1. Esse diagrama é chamado de árvore de recursão, porque ele demonstra como a recursão se comporta e se parece com uma árvore (a raiz está no topo e as folhas na base, então na verdade se parece com uma árvore invertida).
Note que em cada linha do diagrama acima, o número total de elementos é n. Para ver isso, olhe para cada linha individualmente. A primeira linha contém somente uma chamada para mergeSort comum array de tamanho n, então o número total de elementos é n. A segunda linha tem duas chamadas para mergeSort, cada uma com tamanho n / 2. Mas n / 2 + n / 2 = n, então novamente, o número total de elementos é n. Na terceira linha, temos 4 chamadas para as quais são aplicados arrays de tamanho n / 4 cada uma, dando um número total de elementos igual a n / 4 + n / 4 + n / 4 + n / 4, que é igual a 4n / 4 = n. Então, novamente temos n elementos. Agora note que em cada linha nesse diagrama, quem chama as funções tem que fazer uma operação merge nos elementos retornados pelas funções que são chamadas. Por exemplo, o círculo indicado pela cor vermelha tem que ordenar n / 2 elementos. Para fazer isso, ele divide o array de tamanho n / 2 em dois arrays de tamanho n / 4, chama o mergeSort recursivamente para ordená-los (essas chamadas são os círculos indicados em verde), então os une. Essa operação de união tem que unir n / 2 elementos. A cada linha da nossa árvore, o número total de elementos unidos é n. Na linha que acabamos de olhar, nossa função une n / 2 elementos e a função à sua direita (que está em azul) também tem que unir n / 2 elementos. Isso retorna n elementos no total que precisam ser unidos para a linha que estamos olhando.
Por esse argumento, a complexidade de cada linha é de Θ( n ). Sabemos que o número de linhas nesse diagrama, também chamado de profundidade da árvore de recursão, vai ser log( n ). A razão para isso é exatamente a mesma que usamos quando analisamos a complexidade da busca binária. Nós temos log( n ) linhas e cada uma delas é Θ( n ), logo, a complexidade do mergeSort é Θ( n * log( n ) ). Isso é bem melhor do que Θ( n2 ) que tínhamos com o selection sort (lembre-se que log( n ) é bem menor do que n, então n * log( n ) é bem menor do que n * n = n2). Se isso parecer complicado para você, não se preocupe: Não é fácil da primeira vez. Volte para essa seção e leia novamente sobre os argumentos depois de implementar o mergesort na sua linguagem de programação favorita e validar que ele funciona.
Como você viu no último exemplo, análise de complexidade nos permite comparar algoritmos para ver qual é o melhor. Sob essas circunstâncias, nós podemos agora ter certeza de que o merge sort tem uma performance melhor do que o selection sort em arrays grandes. Essa conclusão seria difícil de ser alcançada se não tivéssemos esse background teórico de análise de algoritmos que acabamos de desenvolver. Na prática, os algoritmos que rodam em Θ( n * log( n ) ) são os mais usados. Por exemplo, o kernel Linux usa um algoritmo de ordenação chamado heapsort, que tem o mesmo tempo de execução do mergesort que exploramos aqui, que é Θ( n log( n ) ), então ele é ótimo. Note que nós não provamos que esses algoritmos de ordenação são ótimos. Fazer isso necessita de um argumento matemático mais aprofundado, mas fique tranquilo porque eles não podem ficar melhores de um ponto de vista de complexidade.
Ao terminar de ler esse tutorial, a intuição que você desenvolveu sobre complexidade de algoritmos deve ser capaz de te ajudar a fazer programas melhores e focar os seus esforços de otimização em coisas que realmente importam, no lugar de pequenas coisas que não importam, fazendo o seu trabalho ficar mais produtivo. Além disso, a notação e linguagem matemática que desenvolvemos nesse artigo, como a notação big-O é útil para se comunicar com outros engenheiros de software quando você quiser argumentar sobre o tempo de execução de algoritmos, então você deverá ser capaz de fazer isso com o seu conhecimento recém adquirido.
Sobre
Este artigo está licenciado com uma Licença Creative Commons Atribuição 3.0. Isso significa que você pode copiar/colar, compartilhar, postar no seu site, modificar, e de maneira geral, fazer o que você quiser com ele, desde que mencione o meu nome. Mesmo que você não tenha que fazer isso, se você se basear no meu trabalho, eu o encorajo a publicar seus próprios escritos sob o Creative Commons para ser mais fácil para que outros também compartilhem e colaborem. Da mesma forma, tenho que dar créditos aos trabalhos que usei aqui. Os ícones estilosos que você vê nessa página são os ícones fugue. O lindo padrão listrado que você vê nesse design foi criado por Lea Verou. E, o mais importante, os algoritmos que eu sei, e que me permitiram escrever esse artigo foram ensinados a mim pelos meu professores Nikos Papaspyrou e Dimitris Fotakis.
Atualmente, sou um candidato a PhD na pela Universidade de Atenas. Quando eu escrevi esse artigo, eu era um estudante de graduação em Engenharia Elétrica e Computacional na Universidade Nacional Técnica de Atenas aprendendo software e era coach na Competição Grega de Informática. Na indústria, trabalhei como membro no time de engenharia que fez o deviantART, uma rede social para artistas, nos times de segurança do Google e do Twitter, e em duas start-ups, Zino e Kamibu onde fizermos redes sociais e video games, respectivamente. Me siga no Twitter ou no GitHub se você gostou do artigo, ou mande um e-mail se quiser entrar em contato. Muitos jovens programadores não tem um bom conhecimento em inglês. Mande um e-mail se você quiser traduzir o artigo para a sua língua nativa, para que mais pessoas possam lê-lo.
Obrigado por ler. Eu não fui pago para escrever esse artigo, então se você gostou, me mande um e-mail para dizer oi. Eu gosto de receber imagens de lugares ao redor do mundo, então sinta-se livre para anexar uma foto sua na sua cidade!
Referências
- Cormen, Leiserson, Rivest, Stein. Introduction to Algorithms, MIT Press.
- Dasgupta, Papadimitriou, Vazirani. Algorithms, McGraw-Hill Press.
- Fotakis. Course of Discrete Mathematics at the National Technical University of Athens.
- Fotakis. Course of Algorithms and Complexity at the National Technical University of Athens.

