Een eenvoudige inleiding tot de analyse van de complexiteit van algoritmen
Dionysis "dionyziz" Zindros <dionyziz@gmail.com>Vertaald door Luka Ratic <lukaratic54@gmail.com>
- English
- Ελληνικά
- македонски
- Español
- Nederlands
- עברית
- Português
- srpskohrvatski
- Українська
- Русский
- Help translate
Introductie
Veel programmeurs die de gaafste een handigste software tegenwoordig maken, zoals veel van wat we op internet zien of gebruiken, hebben geen theoretische kennis van informatica. Ze zijn nog steeds erg geweldig een creatief en we bedanken ze voor hun bijdrage.
De theorie van informatica kan echter van pas komen een kan echt praktisch zijn. In deze artikel, gericht op programmeurs die weten wat doen ze maar geen theoretische kennis hebben, ik ga voorleggen een van de meest pragmatische werktuigen van informatica: De Big-O notatie een analyse van algoritmische complexiteit. Als iemand die ook in een academische computer wetenschappelijke-omgeving als in het ontwikkeling van software in de industrie heeft gewerkt, vind ik dit gereedschap echt bruikbaar in praktijk, dus ik hoop dat na het lezen van dit artikel kunt u met uw eigen code deze methoden gebruiken om het beter te maken. Na het lezen van dit text, zullen u ook mogen begrijpen alle van de alledaagse termijnen die computerwetenschappers gebruiken, zoals “Big-O” of “asymptotische gedrag” en “worst-case analyse”.
Deze tekst is ook voor middelbare scholieren en middelbare scholieren uit Griekenland of waar dan ook in de wereld die deelnemen aan de Internationale Informatica-olympiade, een algoritmische competitie voor studenten of andere soortgelijke competities. Als zodanig heeft de text geen wiskundig voorwaarden en het zal u geven de achtergrond die je nodig hebt om verder algoritmen te studeren met en steviger begrip van theorie erachter. Als iemand die vroeger in zulke competities concurrerende Ik raad je zeer aan dat je deze hele tekst lezen en probeer het te begrijpen omdat het zal nodig worden om verder algoritmen en meer geavanceerde technieken te studieren.
Ik geloof deze tekst zal handig zijn ook voor programmeurs in de industrie die niet al te veel kennis van theoretische informatica hebben (Enkele van de meest indrukwekkende programmeurs zijn in feite nooit naar de universiteit gewest). Maar, omdat de tekst ook voor studenten is, zou het kunnen soms zoals uit de leerboek klinken. Bovendien lijken sommige thema’s in deze tekst misschien te voor de hand liggend; bijv. misschien heeft u tijdens middelbare school van het gehoord. Je kunt ze overslaan als je voelt dat je ze begrijpen. Andere secties treden beetje verder in details en iets theoretisch worden want de studenten die in competities zijn moeten ook meer kennis van theoretische algoritmen hebben dan een gemiddelde persoon. Maar ze zijn nog steeds leuk om te weten en niet zo moeilijk te volgen en is het waarschijnlijk je tijd waard. Omdat de originele tekst voor middelbare school studenten was, er is geen wiskundige achtergrond nodig en kan iedereen met sommige programmeer ervaring volgen zonder problemen (d.w.z. je kent wat recursie is).
Door deze artikelen, kunt u verschillende aanwijzingen vinden die linken je op interessante materiaal vaak buiten de domein van de actueel thema. Als je een programmeur in de industrie bent, zullen meest van de concepten al duidelijk zijn. Als je een junior student die deelneemt in een competitie, krijgen je via deze links aanwijzingen van andere gebieden bij informatica or softwareontwikkeling dat je mischien heeft nog niet tegenkomen. Je kunt ernaar kijken om je interesses te verbreden.
Big-O-notatie en algoritmische complexiteitsanalyse zijn ook moeilijk gevonden door professionele programmeurs en eerstejaars studenten, en soms ook als nutteloos vermeden. Maar het is niet zo onmogelijk of theoretisch als het op het eerste gezicht lijkt. Algorithme complexiteit is gewoon een manier om hoe snel een programma of een algorithm is te meten, dus is het echt heel pragmatisch. Laten we beginnen met een beetje motivatie.

Motivatie
We weten nog dat er werktuigen zijn om hoe snel een programma is te meten. Er zijn zogenoemde profilers die meten de looptijd in milliseconden gemeten, en kan ons helpen onze code te optimaliseren door knelpunten op te sporen. Hoewel dit een handig hulpmiddel is, is het niet echt relevant voor de complexiteit van algoritmen. Complexiteit van algoritmen is iets dat is ontworpen om twee algoritmen op idee niveau te vergelijken - het negeren van details op een laag niveau, zoals de programmeertaal voor de implementatie, de hardware waarop het algoritme draait of de instructieset van de gegeven CPU. We willen algoritmen vergelijken in termen van wat ze zijn: ideeën over hoe iets wordt berekend. Milliseconden tellen helpt ons daar niet. Het is heel goed mogelijk dat een slecht algoritme dat is geschreven in een programmeertaal op laag niveau, zoals assembly, veel sneller werkt dan een goed algoritme maar die in een programmeertaal op hoog niveau geschreven is, zoals Python of Ruby. We moeten dus definiëren wat een "beter algoritme" is.
Omdat algoritmen programma's zijn die alleen berekeningen uitvoeren en niet andere dingen die computers ook doen zoals networking of gegevensinvoer en -uitvoer, kunnen we met complexiteitsanalyse meten hoe snel een programma berekeningen doen. Voorbeelden van bewerkingen die puur rekenkundig zijn, zijn onder meer numerieke drijvende-komma bewerkingen zoals optellen en vermenigvuldigen; zoeken binnen een database die past in RAM voor een bepaalde waarde; het pad bepalen dat een artificieel-intelligentiepersonage in een videogame zal doorlopen, zodat ze slechts een korte afstand hoeven te lopen binnen hun virtuele wereld (zie figuur 1); of het uitvoeren van een regex patroon overeenkomst op een string. Het is duidelijk dat berekeningen alomtegenwoordig zijn in computerprogramma's.
Complexiteitsanalyse is ook een hulpmiddel die laat ons overleggen de gedrag van de algoritme als het invoer groter worden. Als we invoeren het algoritme met iets anders, hoe gedraagt de algorithme dan? Als onze algoritme duurt gewoon 1 seconde te een 1000-invoer grote operatie doen, hoe gedraagt de algoritme als de invoer gorete verdubbeld is? Zal het net zo snel, half zo snel of vier keer langzamer lopen? In praktisch programmeren is dit belangrijk omdat we kunnen voorspellen hoe ons algoritme zich zal gedragen wanneer de invoergegevens groter worden. Bijv, als we een algoritme voor een web app heeft gemaakt die goed werkte met 1000 gebruikers en de looptijd ervan meten, kunnen we met behulp van de analyse van algoritmische complexiteit een goed idee hebben van wat er zal gebeuren als we hebben 2000 gebruikers in plaats daarvan. Voor algoritmische competities, het analyse van het complexiteit geeft ons een inzicht over hoe lang onze code loopt voor het grootste testgevallen dat gebruikt zijn om nauwkeurigheid van onze programma te meten. Dus als we het gedrag van ons programma voor een kleine invoer hebben gemeten, kunnen we een goed idee krijgen van hoe het zal gedragen voor grotere invoer. Laten we beginnen met een eenvoudig voorbeeld: het grootste element in een array vinden.
Instructies tellen
In deze artikel, Ik ga gebruiken verschillende programmeertalen voor de voorbeelden. Wanhoop echter niet als u een bijzonder programmeertaal kent niet. Omdat je programmeren kent, je zal mogen zonder problemen de voorbeelden lezen zelfs als je niet bekend bent met de specifieke programmeertaal, omdat ze eenvoudig zullen zijn en ik geen esoterische functies zal gebruiken. Als je een student bent die deelneemt aan algoritme competities, werk je waarschijnlijk met C++ en dus het zou geen probleem moeten zijn om door te gaan. In dat geval raad ik je aan om met C++ te oefenen.
De grootste element op een array can opgezocht zijn met een eenvoudige stuk van code zoals dit voorbeeld in Javascript geschreven is. Met een invoer array A van grootte n:
var M = A[ 0 ];
for ( var i = 0; i < n; ++i ) {
if ( A[ i ] >= M ) {
M = A[ i ];
}
}
Nu is de eerste stap om te tellen hoeveel basisinstructies in deze code worden uitgevoerd. We zullen dit maar eenmaal doen en het zal niet nodig zijn als we onze theorie ontwikkelen, dus heb geduld met me even beetje terwijl we doen dit nu. Terwijl we analyseren dit stuk code, we willen het in eenvoudige instructies breken; Deze kan geëxecuteerd worden recht door de CPU of dicht daarbij. We gaan aannemen dat onze processor de volgende operaties kan elke uitvoeren als één instructie:
- Variabele toewijzen met een waarde
- De waarde van een specifieke element in een array opzoeken
- Twee waarden vergelijken
- Waarde verhogen
- Basische rekenkundige operaties zoals optellen en vermenigvuldigen
We gaan ervan uit dat vertakking (de keuze tussen if en else delen van code nadat de if-voorwaarde geëvalueerd is) vindt plaats onmiddellijk en deze instructies niet meetellen. In de bovenstaande code is de eerste lijn code:
var M = A[ 0 ];
Hier zijn 2 instructies nodig: Een voor A[0] te zoeken, en een voor het toekennen van de waarde aan M (we aannemen dat n altijd minimaal 1 is). Deze twee instructies zijn altijd nodig door het algoritme, onachtzaam de waarde van n. De for lus initialisatiecode moet ook altijd worden uitgevoerd. Dit geeft ons nog twee instructies; een toewijzing en een vergelijking:
i = 0;
i < n;
Deze uitvoeren voor de eerste for lus iteratie. Na elke for lus iteratie we hebben 2 meer instructies nodig uitvoeren, een verhoging van i en een vergelijking om te checken als we binnen de lus blijven:
++i;
i < n;
Dus, als we de lichaam van het lus negeren, de aantal nodige instructies van deze algoritme is 4+ 2n – 4 instructies aan het begin van de for lus en 2 aan het eind bij elke iteratie waarvan we n hebben. Nu kunnen we een wiskundige functie f(n) dat voor een waarde n geeft ons aantal instructies die nodig zijn bij het algorithme. Voor een for lichaam die leeg is, we hebben f(n) = 4+2n.
Worst-case (het slechtste geval) analyse
Kijkend naar de lichaam van de for lus, hebben we een opzoek en een vergelijking die altijd gebeurt:
if ( A[ i ] >= M ) { ...
Dat zijn twee instructies. Maar de if lichaam kan wel of niet worden uitgevoerd, afhankelijk aan wat de waarden van de arrays zijn. Als het zo is dat A[i] >= M, dan voeren we twee meer instructies uit – een array opzoek en een toewijzing:
M = A[ i ]
Maar nu we kunnen niet een f(n) zo gemakkelijk definiëren, omdat het aantal instructies niet alleen afhangt van n, maar ook van de invoerwaarde. Bijvoorbeeld, voor A = [1, 2, 3, 4], de algoritme zal meer instructies nodig hebben dan in geval dat A = [4, 3, 2, 1]. Bij het analyseren van algoritmen houden we vaak rekening met de worst case scenario. Wat is het ergste dat kan gebeuren met ons algoritme? Wanneer heeft onze algoritme de meeste instructies nodig om te uitvoeren? In dit gevaar, het is wanneer we een array oplopende volgorde hebben zoals A = [1, 2, 3, 4]. In dit geval moet de M elke keer worden vervangen om de meeste instructies te geven. Computerwetenschappers hebben een fancy naam voor dat – de worst-case analyse; Dat is rekening houden met het slechtst mogelijke scenario, wanneer we niet veel geluk hebben. Dus in het slechtste geval hebben we 4 instructies die in de lichaam van de for lus worden uitgevoerd, dus we hebben f (n) = 4 + 2n + 4n = 6n + 4. Deze functie f, waarbij de waarde van het probleem wordt aangenomen van grootte n, geeft ons het aantal instructies dat nodig is in het slechtste geval.
Asymptotisch gedrag
Als we zo'n functie nemen, hebben we een heel goed idee van hoe snel het algoritme eigenlijk is. Zoals ik beloofde, hoeven we ons echter niet bezig te houden met de nauwgezette berekening van het aantal instructies in ons programma. Bovendien hangt het werkelijke aantal processor instructies dat nodig is voor de programmeertaal expressie af van de compiler van onze programmeertaal en van de set processor instructies (dwz is het AMD of Intel Pentium op uw pc of is het MIPS op Playstation 2) en we hebben gezegd dat we het zullen negeren. We zullen nu onze functie f overslaan via een "filter" dat ons zal helpen om kleine details te verwijderen die computerwetenschappers pretenderen te negeren.
Op onze functie, 6n+4, hebben we twee termen: 6n en 4. Bij complexiteitsanalyse is het enige dat voor ons van belang is, wat er gebeurt met de functie die de instructies telt als de invoerwaarde (n) groeit. Dit gaat echt samen met de eerdere ideeën over gedrag bij de "worst-case scenario": we zijn geïnteresseerd in hoe ons algoritme zich gedraagt wanneer het slecht wordt behandeld; wanneer het wordt uitgedaagd om iets moeilijks te doen. Let op dat dit echt handig is bij het vergelijken van algoritmen. Als het ene algoritme het andere inhaalt met een hogere invoerwaarde, blijft het waarschijnlijk waar dat een sneller algoritme sneller blijft als een eenvoudigere, kleinere invoerwaarde wordt gegeven. Van de termen die we overwegen, zullen we alle termen verwijderen die langzaam groeien, zodat alleen blijven de termen die snel groeien naarmate de waarde van n toeneemt. Het is duidelijk dat 4 een 4 blijft terwijl de waarde van n groter wordt, maar 6n groter en groter wordt, dus het neigt er steeds meer toe te doen voor grotere problemen. Daarom is het eerste dat we zullen doen de 4 laten vallen en de functie behouden als f(n) = 6n.
Dit is wel logisch als je erover denkt, zoals 4 gewoon een initialisatie constant is. Programmeertalen kunnen verschillen, afhankelijk van de tijd dat ze nodig hebben om te ingesteld worden. Java heeft bijvoorbeeld wat tijd nodig om hun virtual machine te initialiseren. Omdat we de verschillen tussen programmeertalen negeren, is het logisch om deze waarde te negeren.
Het tweede wat we negeren is de constante die n vermenigvuldigt, dus krijgt onze functie de vorm f(n) = n. Zoals je kunt zien, vereenvoudigt dit de zaken behoorlijk. Nogmaals, het is logisch om deze constante te laten vallen als we nadenken over hoe verschillende programmeertalen compileren. De array zoek in een programmeertaal kan in een andere taal anders worden gecompileerd. Bijvoorbeeld, voor A[i], C controleert niet of de waarde in het bereik van de grootte van die string ligt, terwijl Pascal dat wel doet.
M := A[ i ]
Dit is het equivalent van het volgende in C:
if ( i >= 0 && i < n ) {
M = A[ i ];
}
Het is redelijk om te verwachten dat verschillende programmeertalen verschillende factoren hebben bij het tellen van hun instructies. In ons voorbeeld waarin we een “domme compiler” voor Pascal gebruiken die zich niet bewust is van mogelijke optimalisaties, vereist Pascal 3 instructies voor elke array toegang in plaats van de 1 instructie die C vereist. De uitsluiting van deze factor komt overeen met het feit dat er verschillen zijn tussen programmeertalen en compilers en dat we uitsluitend het idee van het algoritme zelf analyseren.
Dit filter van "alle factoren laten vallen" en "de grootste groei term behouden", zoals hierboven beschreven, is wat we asymptotisch gedrag noemen. Dus het asymptotische gedrag van f(n) = 2n + 8 wordt beschreven door de functie f(n) = n. In wiskundige termen gesproken, we zijn geïnteresseerd in de limiet van functie f aangezien n naar oneindig neigt; maar als je niet begrijpt wat die zin formeel betekent, wees dan niet bang, want dit is alles wat je moet weten. (Hoewel we in een strikt wiskundige setting niet in staat zouden zijn om de constanten in de limiet te laten vallen, maar in de informatica willen we dat doen om de hierboven beschreven redenen.) Laten we aan een paar voorbeelden werken om het concept beter te begrijpen.
Laten we vinden de asymptotische gedrag van de volgende voorbeeldfunctie door constantie laten vallen en de termen te behouden die het snelst groeien.
f( n ) = 5n + 12 geeft f( n ) = n.
Volgens exact dezelfde redenering als hierboven.
f( n ) = 109 geeft f( n ) = 1.
We laten de vermenigvuldiger 109 * 1 vallen, maar we moeten hier nog steeds een 1 plaatsen om aan te geven dat deze functie een waarde heeft die niet nul is.
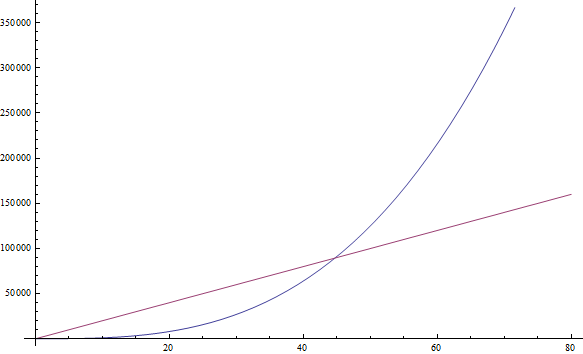
f( n ) = n2 + 3n + 112 geeft f( n ) = n2
Hier wordt n2 groter dan 3n voor voldoende grote n, dus dat houden we.
f( n ) = n3 + 1999n + 1337 geeft f( n ) = n3
Hoewel de factor voor n vrij groot is, kunnen we toch een voldoende grote n vinden zodat n3 groter is dan 1999n. Omdat we geïnteresseerd zijn in het gedrag voor zeer grote waarden van n, behouden we alleen n3 (zie figuur 2).
f( n ) = n +
 geeft f( n ) = n
geeft f( n ) = nDit is zo omdat n sneller groeit dan
 als we n vergroten.
als we n vergroten.
U kunt de volgende voorbeelden zelf uitproberen:
Oefening 1
- f( n ) = n6 + 3n
- f( n ) = 2n + 12
- f( n ) = 3n + 2n
- f( n ) = nn + n
(Schrijf je resultaten op; de oplossing staat hieronder)
Als je problemen hebt met een van de bovenstaande, vul dan een grote n in en kijk welke term groter is. Eenvoudig, toch?
Complexiteit
Dit betekent dat, aangezien we al deze decoratieve constanten kunnen laten vallen, het heel gemakkelijk is om asymptotisch gedrag te vinden voor een instructie-tellende functie van een programma. In feite, elk programma dat geen lussen heeft, zal f(n) = 1 hebben, aangezien het aantal instructies dat het nodig heeft slechts een constante is (tenzij het recursie gebruikt). Elk programma met een enkele lus die van 1 naar n gaat, heeft f(n) = n, omdat het een constant aantal instructies vóór de lus heeft, een constant aantal instructies na de lus en een constant aantal instructies binnen de lus die allemaal n keer worden uitgevoerd.
Dit zou nu veel gemakkelijker en minder vervelend moeten zijn dan het tellen van individuele instructies, dus laten we een paar voorbeelden bekijken om vertrouwd te raken met het concept. Het volgende PHP programma controleert of een bepaalde waarde bestaat binnen een array A van grootte n:
<?php
$exists = false;
for ( $i = 0; $i < n; ++$i ) {
if ( $A[ $i ] == $value ) {
$exists = true;
break;
}
}
?>
Dit methode zoeken voor een waarde binnen een array heet lineair zoeken. Dit is een redelijke naam, aangezien dit programma f( n ) = n heeft (we zullen in de volgende sectie precies begrijpen wat "lineair" betekent). Je merkt misschien dat hier een break-statement is dat kan onze programma eerder beëindigen, zelfs na slechts een iteratie. Maar onthoud dat we op zoek zijn naar het worst case scenario, waarvoor dit programma in array A niet de waarde heeft die we zoeken. We hebben dus nog steeds dat f (n) = n.
Oefening 2
Analyseer systematisch het aantal instructies in de bovenstaande PHP-code, in het slechtste geval f (n) voor de waarde van n, vergelijkbaar met de analyse die we deden voor ons eerste programma in Javascript. Bevestig vervolgens dat de asymptotische f (n) = n.
Laten we een Python programma kijken dat twee array elementen toevoegt om een som te produceren die in een andere variabele wordt opgeslagen:
v = a[ 0 ] + a[ 1 ]
Hier hebben we een constant aantal instructies, dus f(n) = 1.
Het volgende programma dat in C++ is geschreven, controleert of een vector (een fancy array) met de naam A en de grootte n, twee dezelfde waarden bevat:
bool duplicate = false;
for ( int i = 0; i < n; ++i ) {
for ( int j = 0; j < n; ++j ) {
if ( i != j && A[ i ] == A[ j ] ) {
duplicate = true;
break;
}
}
if ( duplicate ) {
break;
}
}
Omdat we hier twee geneste lussen in elkaar hebben, hebben we een asymptotisch gedrag f(n) = n2.
Vuistregel:Eenvoudige programma's kan geanalyseerd worden door geneste lussen te tellen. Een lus over n elementen geeft f(n) = n. Een lus binnen een lus geeft f(n) = n2. Een lus binnen een andere lus dat binnen het derde lus ligt geeft f(n) = n3, enzovoort.
Als we een programma hebben dat een functie binnen een lus aanroept en we weten hoeveel instructies de aangeroepen functie uitvoert, is het gemakkelijk om het aantal instructies van het hele programma te krijgen. Laten we inderdaad eens kijken naar dit voorbeeld dat in C geschreven is:
int i;
for ( i = 0; i < n; ++i ) {
f( n );
}
Als we weten dat f(n) een functie is die precies n instructies uitvoert, kunnen we weten dat het aantal instructies van het hele programma asymptotisch n2 is, aangezien de functie precies n keer wordt aangeroepen.
Vuistregel: Als we een reeks for-lussen hebben die op een rij gaan, bepaalt de langzaamste ervan hoe het programma zich asymptotisch zal gedragen. De twee geneste lussen gevolgd door één gewone lus zijn hetzelfde als die twee geneste lussen alleen, aangezien de geneste lussen de overhand hebben op de eenvoudige lus.
Nu, laten we overschakelen naar de fancy notatie die in gebruik is met computerwetenschappers. Als we f asymptotisch hebben opgehelderd, zeggen we dat ons programma Θ(f(n)) is. Bijvoorbeeld, de programma’s hierboven zijn Θ(1), Θ(n2) en Θ(n2) respectievelijk. Θ(n) wordt uitgesproken als “Theta van n”. We zeggen weleens dat f(n), de originele functie die instructies telt, samen met de constanten Θ( iets ) is. We kunnen bijvoorbeeld zeggen dat f(n) = 2n een functie is die Θ(n) is — niets nieuws. We kunnen ook schrijven 2n ∈ Θ(n), dat wordt uitgesproken als "twee n is theta van n". Laat u niet verwarren door deze notatie, want het betekent alleen dat als we het aantal noodzakelijke instructies hebben geteld en dat 2n is, het asymptotische gedrag van ons algoritme wordt beschreven door n, die we hebben gevonden door de constanten weg te laten. Met deze notatie, de volgende wiskundige uitspraken zijn waar:
- n6 + 3n ∈ Θ( n6 )
- 2n + 12 ∈ Θ( 2n )
- 3n + 2n ∈ Θ( 3n )
- nn + n ∈ Θ( nn )
Trouwens, als je oefening 1 hebt opgelost, zijn dit precies de antwoorden die je had moeten vinden.
We noemen deze functie, d.w.z. wat nemen we binnen Θ( hier ), de tijdscomplexiteit of gewoon de complexiteit van onze algoritme. Dus, een algoritme met Θ(n) heeft complexiteit n. We hebben ook speciale namen voor Θ(1), Θ(n), Θ(n2) and Θ(log(n)) omdat we ze heel vaak zien. Een algoritme met Θ(1) is een constant-tijd algoritme, Θ(n) is een lineair algoritme, Θ(n2) is kwadratisch en dat Θ(log(n)) algoritmisch is (geen zorgen maken als je niet weet wat logaritmen zijn, er is een uitleg verderop in de tekst.)
Vuistregel: Programma’s met een grotere Θ uitvoeren langzamer dan die met een kleinere Θ.

Big-O notatie
Het is soms waar dat het voor complexere voorbeelden moeilijk zal zijn om precies het gedrag van een algoritme te bevatten zoals we hierboven hebben gedaan. Maar we zullen wel kunnen zeggen dat het gedrag van ons algoritme nooit een exacte grens zal overschrijden. Dit zal leven voor ons meer mogelijk maken omdat we zullen niet moeten precies zeggen hoe snel onze algoritme zal uitvoeren zelfs als we konstanten gaan negeren zoals we eerder deden. Alle dat we moeten doen is een bepaalde grens te vinden. Dit kan uitgelegd worden met een voorbeeld.
Een welbekend probleem dat computerwetenschappers hun studenten geven is dat van sorteren. Bij sorteren wordt een array A van grotte n gegeven (Klinkt bekend?) en we gevraagd zijn om een programma te schrijven om dit array te sorteren. Het probleem is heel interessant omdat bij echte systemen is het pragmatisch. Bijv. een “file explorer” moet bestanden op naam sorteren zodat de gebruiker er beter door kan navigeren. Of, in een ander voorbeeld, een videogame moet 3D-objecten die in de wereld worden weergegeven sorteren op basis van hun afstand vanuit het perspectief van de speler, binnen de virtuele wereld om te bepalen wat zichtbaar is en wat niet, iets dat het zichtbaarheids probleem wordt genoemd (zie figuur 3). De objecten die zich het dichtst bij de speler bevinden, zijn de zichtbare, terwijl de objecten die verder weg zijn verborgen kunnen worden door de objecten voor hen. Sorteren is ook interessant omdat er zijn ook wel algoritmen waarmee het kan gedaan zijn, sommige erger dan andere. Het is ook een probleem dat eenvoudig is om te definiëren en uitleggen. Laten we dus een code schrijven dat een array sorteert.
Hier is een inefficiënte manier om arrays te sorteren in Ruby. (Ruby ondersteunt natuurlijk array sorteren met ingebouwde functies die u in plaats daarvan zou moeten gebruiken, en die zeker sneller zijn dan wat we hier zullen zien. Maar dit is hier ter illustratie.)
b = []
n.times do
m = a[ 0 ]
mi = 0
a.each_with_index do |element, i|
if element < m
m = element
mi = i
end
end
a.delete_at( mi )
b << m
end
Dit method heet selection sort. Het vindt de minimum van onze array (de array wordt hierboven aangegeven met a, terwijl de minimumwaarde wordt aangegeven met m en mi is de index), het plaatst het dan aan het einde van een nieuwe array (in ons geval b), en verwijdert het uit de originele array. Dan vindt het het minimum tussen de resterende waarden van onze originele array, voegt het vervolgens toe aan onze nieuwe array zodat het nu twee elementen bevat en verwijdert het uit onze originele array. Het gaat door met dit proces totdat alle items uit het origineel array verwijderd zijn en in de nieuwe array zijn ingevoegd. Dan is het array gesorteerd. Bij deze voorbeeld we kunnen zien dat er twee geneste lussen zijn. De buitenste lus loopt n keer en de binnenste lus loopt eenmaal voor elk element van de a array. Terwijl de array a aan het begin n items heeft, verwijderen we een element uit de array in elke iteratie. Dus de binnenste lus herhaalt zich n keer tijdens de eerste iteratie van de buitenste lus, dan n - 1 keer, dan n - 2 keer enzovoort, tot de laatste iteratie van de buitenste lus waarin het maar een keer loopt.
Het is een beetje moeilijker om de complexiteit van dit programma te bereken omdat we de som 1 + 2 + ... + (n - 1) + n moeten berekenen. Maar we kunnen er zeker een "bovengrens" vinden. D.w.z we kunnen ons programma wijzigen (je kunt dat in je hoofd doen, niet in de eigenlijke code) om het erger te maken dan het is en dan de complexiteit van dat nieuwe programma vinden. Als we kunnen de complexiteit van de slechtste programma die we hebben geconstrueerd vinden, dan weten we dat ons origineel programma hoogstens zo slecht is, of misschien wel beter. Dus als we ontdekken dat de complexiteit van het nieuwe programma erg goed is, en dat het erger is dan de complexiteit van het originele programma, kunnen we erop rekenen dat ons originele programma een solide complexiteit heeft - ofwel even goed als het slechtere programma dat we hebben gemaakt, of beter.
Laten we nu een manier vinden om dit voorbeeldprogramma te bewerken om het gemakkelijker te maken om de complexiteit ervan te achterhalen. Maar laten we in gedachten houden dat we het alleen maar erger kunnen maken, d.w.z. meer instructies toevoegen, zodat onze schatting zinvol is voor ons origineel programma. Uiteraard kunnen we de interne lus van het programma zo veranderen dat het altijd precies n keer wordt herhaald in plaats van een ander aantal keren. Als we het gewoon zo veranderen, dan is het nieuwe algoritme dat we hebben geconstrueerd duidelijk Θ(n2), omdat we twee geneste lussen hebben waar elk precies n keer wordt herhaald. Als dat zo is, zeggen we dat het oorspronkelijke algoritme O(n2) is. O(n2) wordt “Big O van n kwadraat” uitgesproken. Dit betekent dat ons programma asymptotisch niet slechter is dan n2. Het kan zelfs beter zijn dan dat, of het kan hetzelfde zijn als dat. Trouwens, als ons programma inderdaad Θ(n2) is, kunnen we nog steeds zeggen dat het O(n2) is. Om dit te helpen realiseren, stel je voor dat je het originele programma zodanig wijzigt dat het niet veel verandert, maar het toch een beetje erger maakt, zoals het toevoegen van een betekenisloze instructie aan het begin van het programma. Als u dit doet, verandert de functie die de instructies telt, door een eenvoudige constante, die wordt genegeerd als het gaat om asymptotisch gedrag. Dus een programma dat Θ(n2) is, is ook O(n2).
Maar een programma dat O(n2) is misschien niet Θ(n2). Elk programma dat bijvoorbeeld Θ(n) is, is naast O(n) ook O(n2). Als we ons voorstellen dat een Θ(n) programma een eenvoudige for-lus is die n keer wordt herhaald, kunnen we het erger maken door het in een andere for-lus te stellen die ook n keer wordt herhaald, waardoor een zo een programma krijgen met f(n) = n2. Om dat te generaliseren, elk programma dat Θ(a) is, is ook O(b), wanneer b slechter is dan a. Merk op dat ons gewijzigde programma moet niet zinvol of gelijkwaardig te zijn aan het originele programma. Het hoeft alleen meer instructies uit te voeren dan het origineel voor een gegeven n. We gebruiken het alleen voor het tellen van instructies, niet het oplossen van ons probleem.
Dus, om te zeggen dat ons programma O(n2) is, is aan de veilige kant: we hebben ons algoritme geanalyseerd en we hebben ontdekt dat het nooit slechter is dan n2. Maar het kan zijn dat het in feite n2 is. Dit geeft ons een goede inschatting van hoe snel ons programma loopt. Laten we een paar voorbeelden bekijken om vertrouwd te raken met deze nieuwe notatie.
Oefening 3
Vinden welke van de volgende waar is:
- Een Θ( n ) algoritme is O( n )
- Een Θ( n ) algoritme is O( n2 )
- Een Θ( n2 ) algoritme is O( n3 )
- Een Θ( n ) algoritme is O( 1 )
- Een O( 1 ) algoritme is Θ( 1 )
- Een O( n ) algoritme is Θ( 1 )
Oplossing
- We weten dat dit waar is aangezien ons origineele programma Θ(n) was. We kunnen O(n) bereiken zonder ons programma te veranderen.
- Aangezien n2 slechter is dan n, is dit waar.
- Aangezien n3 slechter is dan n2, is dit waar.
- Aangezien 1 niet slechter dan n is, dit is niet waar. Als een programma n instructies asymptotisch opneemt (een lineair aantal instructies), we kunnen het niet erger maken en het slechts 1 instructie asymptotisch laten nemen (een constant aantal instructies).
- Dit is waar aangezien de twee complexiteiten hetzelfde zijn.
- Dit kan misschien waar of niet waar zijn, afhankelijk van de algoritme. In de algemeene geval, dat is niet waar. Als een algoritme Θ(1) is, dan is het duidelijk dat het niet O(n) is. Maar als het O(n) is dan het mischien kan niet Θ(1) zijn. Bijv. een Θ(n) algoritme is O(n) maar niet Θ(1).
Oefening 4
Met hulp van rekenkundige progressie bewijs dat bovenstaand programma niet alleen O(n2) maar ook Θ(n2) is. Als je niet weet wat een rekenkundige progressie is, zoek het dan op op Wikipedia – het is gemakkelijk.
Omdat de O-complexiteit van een algoritme ons een bovengrens geeft voor het echte complexiteit van de programma, terwijl Θ geeft ons de echte complexiteit van de algoritme, zeggen we soms dat Θ ons een strakke grens geeft. Als we weten dat we een complexiteit grens hebben gevonden die niet strak is, kunnen we ook een kleine letter o gebruiken om dat aan te duiden. Als een algoritme bijvoorbeeld Θ(n) is, dan is de strakke complexiteit n. Dan is dit algoritme zowel O(n) als O(n2). Aangezien het algoritme Θ(n) is, is de grens hier O(n) strak. Maar de O(n2) grens is niet strak, en dus kunnen we schrijven dat het algoritme o(n2) is, wat wordt uitgesproken als "kleine o van n kwadraat" om te illustreren dat we weten dat onze grens niet strak is. Het is beter als we strakke grenzen voor onze algoritmen kunnen vinden, omdat deze ons meer informatie geven over hoe ons algoritme zich gedraagt, maar het is niet altijd gemakkelijk om te doen.
Oefening 5
Bepaal welke van de volgende grenzen strak zijn en welke niet. Controleer of er iets niet klopt. Gebruik o(notatie) om grenzen te illustreren die niet strak zijn.
- Een Θ(n) algoritme waarvoor we een O(n) bovengrens hebben gevonden.
- Een Θ(n2) algoritme waarvoor we een O(n3) bovengrens hebben gevonden.
- Een Θ(1) algoritme waarvoor we een O( n) bovengrens hebben gevonden.
- Een Θ(n) algoritme waarvoor we een O(1) bovengrens hebben gevonden.
- Een Θ(n) algoritme waarvoor we een O(2n) bovengrens hebben gevonden.
Oplossing
- In dit geval zijn de Θ complexiteit en de O complexiteit hetzelfde, dus de grens is strak.
- Hier zien we dat de O complexiteit groter is dan de Θ complexiteit, dus deze grens is niet strak. Inderdaad, een grens van O(n2) zou strak zijn. We kunnen dus schrijven dat het algoritme o(n3) is.
- Nogmaals, we zien dat de O complexiteit groter is dan de Θ complexiteit, dus we hebben een grens die niet strak is. Een grens van O(1) zou strak zijn. We kunnen er dus op wijzen dat de O(n) grens niet strak is door deze te schrijven als o(n).
- We moeten een fout hebben gemaakt bij het berekenen van deze grens, want het is verkeerd. Het is onmogelijk voor een Θ(n) algoritme om een bovengrens van O(1) te hebben, aangezien n een grotere complexiteit is dan 1. Onthoud dat O een bovengrens geeft.
- Dit lijkt misschien een niet strak grens, maar dit is eigenlijk niet waar. Deze grens is namelijk strak. Onthoud dat het asymptotische gedrag van 2n en n hetzelfde is, en dat O en Θ alleen betrekking hebben op asymptotisch gedrag. We hebben dus dat O(2n) = O(n) en daarom is deze grens strak omdat de complexiteit hetzelfde is als de Θ.
Vuistregel: Het is eenvoudiger om een O-complexiteit te berekenen dan een Θ-complexity.
Je bent nu misschien een beetje overweldigd door al deze notaties, maar laten we nog twee symbolen introduceren voordat we verder gaan met een paar voorbeelden. Deze zijn gemakkelijk nu je Θ, O en o kent, en we zullen ze niet veel later in dit artikel gebruiken, maar het is goed om ze te kennen. In het bovenstaande voorbeeld hebben we ons programma gewijzigd om het erger te maken (d.w.z. meer instructies te nemen en dus meer tijd) en de O-notatie gemaakt. O is geweldig omdat het ons vertelt dat ons programma nooit langzamer zal zijn dan een bepaalde grens, en het geeft dus waardevolle informatie zodat we kunnen rechtvaardigen dat ons programma goed genoeg is. Als we het tegenovergestelde doen en ons programma veranderen om het beter te maken en de complexiteit van het resulterende programma berekenen, gebruiken we Ω. Ω geeft ons daarom een complexiteit waarbij we weten dat ons programma niet beter zal zijn dan wat we hebben. Dit is handig als we willen bewijzen dat een algoritme inefficiënt is, misschien voor een bepaald geval. Bijvoorbeeld, als u zegt dat een algoritme Ω(n3) is, betekent dit dat het algoritme niet beter is dan n3. Het kan Θ( n3 ) zijn, net zo erg als Θ(n4) of nog erger, maar we weten dat het in wezen slecht is. Dus Ω geeft ons een ondergrens voor de complexiteit van ons algoritme. Net als met “ο” kunnen we ω schrijven als we weten dat onze grens niet strak is. Bijvoorbeeld, een Θ(n3) algoritme is ο(n4) en ω(n2). Ω(n) wordt uitgesproken als "grote omega van n", en ω(n) wordt uitgesproken als "kleine omega van n".
Oefening 6
Neem voor de volgende Θ complexiteiten een strakke en een niet-strakke O grens, en een strakke en niet-strakke Ω grens, op voorwaarde dat deze bestaan.
- Θ( 1 )
- Θ(
 )
) - Θ( n )
- Θ( n2 )
- Θ( n3 )
Oplossing
Dit is een duidelijke gebruik van de bovenstaande definities.
- De strakke grenzen zullen O(1) en Ω(1) zijn. Een niet strakke O grens zal O(n) zijn. Onthoud dat O ons een bovengrens geeft. Aangezien n groter is dan 1 is dit een niet-strakke grens en kunnen we deze ook als o(n) schrijven. Maar we kunnen geen niet-strakke grens voor Ω vinden, omdat we voor deze functies niet lager dan 1 kunnen krijgen. Dus we hebben alleen de strakke grens.
- De strakke grenzen zullen hetzelfde moeten zijn als de Θ complexiteit, dus zijn ze respectievelijk O(
 ) en Ω(
) en Ω(  ). Voor niet-strakke grenzen kunnen we O( n ) hebben, aangezien n groter is dan
). Voor niet-strakke grenzen kunnen we O( n ) hebben, aangezien n groter is dan  en het dus een bovengrens is voor
en het dus een bovengrens is voor  . Omdat we weten dat dit een niet-strakke bovengrens is, kunnen we deze ook schrijven als o( n ). Voor een ondergrens die niet strak is, kunnen we gewoon Ω( 1 ) gebruiken. Omdat we weten dat deze grens niet strak is, kunnen we deze ook schrijven als ω( 1 ).
. Omdat we weten dat dit een niet-strakke bovengrens is, kunnen we deze ook schrijven als o( n ). Voor een ondergrens die niet strak is, kunnen we gewoon Ω( 1 ) gebruiken. Omdat we weten dat deze grens niet strak is, kunnen we deze ook schrijven als ω( 1 ). - De strakke grenzen zijn O( n ) en Ω ( n ). Twee niet-strakke grenzen kunnen ω( 1 ) en o( n3) zijn. Dit zijn in feite vrij slechte grenzen, omdat ze verre van de origineele complexiteit zijn, maar ze zijn nog steeds geldig met behulp van onze definities.
- De strakke grenzen zijn O(n2) en Ω(n2). Voor niet-strakke grenzen kunnen we opnieuw ω(1) en o(n3) gebruiken zoals in ons vorige voorbeeld.
- De strakke grenzen zijn respectievelijk O(n3) en Ω(n3). Twee niet-strakke grenzen kunnen ω(
 n2 ) en o o(
n2 ) en o o(  n3 ) zijn. Hoewel deze grenzen niet strak zijn, zijn ze beter dan degene die we hierboven gaven.
n3 ) zijn. Hoewel deze grenzen niet strak zijn, zijn ze beter dan degene die we hierboven gaven.
De reden dat we O en Ω gebruiken in plaats van Θ, hoewel O en Ω ook strakke grenzen kunnen geven, is dat we misschien niet kunnen zeggen of een grens die we hebben gevonden strak is, of dat we het proces misschien niet willen doorlopen om het zo te onderzoeken.
Als je niet alle symbolen volledig onthoudt en waarvoor ze worden gebruikt, maak je er dan nu niet al te veel zorgen over. Je kunt altijd terugkomen en opnieuw lezen. De belangrijkste symbolen zijn O en Θ.
Merk ook op dat hoewel Ω ons een ondergrens gedrag voor onze functie geeft (d.w.z. we hebben ons programma verbeterd zodat het minder instructies uitvoert), we nog steeds verwijzen naar een "worst-case" analyse. De reden is dat we ons programma de slechtst mogelijke input geven voor een gegeven n en het gedrag ervan analyseren onder deze veronderstelling.
De volgende tabel toont de symbolen die we zojuist hebben geïntroduceerd en hun equivalenten met de gebruikelijke wiskundige vergelijking symbolen die we voor getallen gebruiken. De reden waarom we hier niet de gebruikelijke symbolen gebruiken en in plaats daarvan Griekse letters gebruiken, is om erop te wijzen dat we een asymptotische vergelijking van gedrag maken, niet alleen een eenvoudige vergelijking.
| Asymptotische vergelijkingsoperator | Numerieke vergelijkingsoperator |
|---|---|
| Ons algoritme is o( iets ) | Een getal is < iets |
| Ons algoritme is O( iets ) | Een getal is ≤ iets |
| Ons algoritme is Θ( iets ) | Een getal is = iets |
| Ons algoritme is Ω( iets ) | Een getal is ≥ iets |
| Ons algoritme is ω( iets ) | Een getal is > iets |
Vuistregel: Vuistregel: Hoewel O, o, Ω, ω en Θ soms nuttig zijn, wordt O het meest gebruikt omdat het gemakkelijker is af te leiden van Θ en meer praktisch dan Ω.
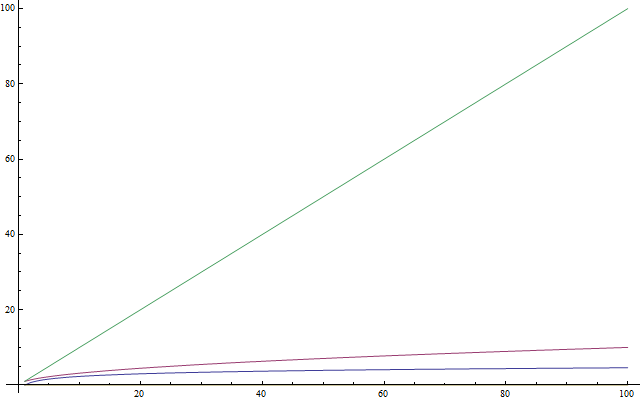
Logaritmen
Als u weet wat logaritmen zijn, kunt u deze sectie overslaan. Omdat veel mensen niet bekend zijn met logaritmen, of ze de laatste tijd niet veel hebben gebruikt en ze zich ze niet meer herinneren, is deze sectie hier als een introductie of herhaling voor hen. Deze tekst is ook voor jongere studenten die nog geen logaritmen op school hebben gezien. Logaritmen zijn van heel belang, omdat ze komen vaak met complexiteitsanalyse. Een logaritme is een operatie dat op een getal toegepast wordt die het heel klein maakt – zoon net als een vierkantswortel van een getal. Zo als er een ding is dat je over logaritmen moet herinneren is dat ze nemen een getal en maken het veel kleiner dan het origineel (zie figuur 4). Nu, op dezelfde manier dat de vierkantswortel inverse operaties zijn van iets kwadrateren, de logaritmen zijn het inverse van machtsverheffing. Het is niet zo moeilijk als het klinkt. Het is beter uitgelegd door een voorbeeld. Beschouw de volgende vergelijking:
2x = 1024
We willen nu de vergelijking voor x oplossen. Zo, we vragen ons af: Wat is het getal waartoe we grondtal 2 moeten verhogen zodat we 1024 krijgen? De getal is 10. En, inderdaad, we hebben dat 210 = 1024, wat gemakkelijk te verifiëren is. Logaritmen helpen ons dit probleem te presenteren met behulp van nieuwe notatie. In dit geval is 10 de logaritme van 1024 en we schrijven dit als log( 1024 ) en lezen we het als "de logaritme van 1024". Omdat we 2 als onze grondtal gebruiken, deze logaritmen zijn “logaritmen met grondtal 2” genoemd. Er zijn ook logaritmen in andere grondtallen, maar we zullen in dit artikel alleen logaritmen met base 2 gebruiken. Als je een student bent die deelneemt aan internationale competities en je weet niets van logaritmen, raad ik je ten zeerste aan om je logaritmen te oefenen na het lezen van dit artikel. In informatica zijn logaritmen met grondtal 2 de meest voorkomende. Dit komt omdat we vaak maar twee verschillende entiteiten hebben: 0 en 1. We halveren ook één groot probleem, waarvan er altijd twee delen zijn. U hoeft dus alleen kennis te hebben van logaritmen met grondtal 2 om door te gaan met dit artikel.
Oefening 7
Los de onderstaande vergelijkingen op. Geef in ieder geval aan welke logaritme je vindt. Gebruik alleen logaritmen met grondtal 2.
- 2x = 64
- (22)x = 64
- 4x = 4
- 2x = 1
- 2x + 2x = 32
- (2x) * (2x) = 64
Oplossing
We hebben niets meer nodig dan de toepassing van de hierboven gedefinieerde ideeën.
- Met trial-and-error kunnen we ontdekken dat x = 6 en dus log(64) = 6.
- Hier zien we dat (22)2, vanwege de eigenschappen van exponenten, ook kan worden geschreven als 22x. Dus we krijgen dat 2x = 6 omdat log(64) = 6 uit ons eerdere voorbeeld, en dus x = 3.
- Met behulp van onze kennis van de eerdere vergelijking, kunnen we 4 als 22 schrijven en dus wordt onze vergelijking (22)2 = 4, wat dezelfde is als 22x = 4. Dan merken we dat log(4) = 2 omdat 22 = 4, n dus krijgen we dat 2x=2, dus x=1. Dit is gemakkelijk te zien aan de hand van de originele vergelijking, aangezien het gebruik van een exponent van 1 de basis als resultaat oplevert.
- Onthoud dat een exponent van 0 een resultaat van 1 oplevert. Dus we hebben log( 1 ) = 0 als 20 = 1, en dus x = 0.
- Hier hebben we een som en zo kunnen we niet direct de logaritme krijgen. Merken we echter dat 2x + 2x = 2 * (2x). Dus we hebben vermenigvuldigd met nog eens twee, en daarom is dit hetzelfde als 2x+1 en nu hoeven we alleen nog maar de vergelijking 2x + 1 = 32 op te lossen. We vinden dat log( 32 ) = 5 en dus x + 1 = 5 en dus x = 4.
- We vermenigvuldigen twee 22x met elkaar, dus we kunnen ze verbinden door op te merken dat (2x) * (2x) hetzelfde is als 22x. Dan hoeven we alleen nog maar de vergelijking 22x = 64 op te lossen die we hierboven al hebben opgelost en dus x = 3.
Vuistregel: Voor algoritmen die je schrijft voor wedstrijden in C++, kun je, nadat je je complexiteit hebt geanalyseerd, inschatten hoe snel je programma zal draaien door te verwachten dat het ongeveer 1.000.000 bewerkingen per seconde uitvoert, waarbij de bewerkingen die je telt worden gegeven door de asymptotische gedragsfunctie het beschrijven van uw algoritme. Een Θ( n) algoritme heeft bijvoorbeeld ongeveer een seconde nodig om de invoer voor n = 1.000.000 te verwerken.
Recursieve complexiteit
Laten we nu kijken naar een recursieve functie. Een recursieve functie is een functie die zichzelf aanroept. Kan we de complexiteit ervan analyseren? De volgende functie die in python geschreven is evalueert een faculteit van een getal. De faculteit van een positief geheel getal wordt gevonden door deze te vermenigvuldigen met alle voorgaande positieve gehele getallen samen. De faculteit van 5 is bijvoorbeeld 5 * 4 * 3 * 2 * 1. We schrijven dat als "5!" en spreek het uit als "vijf faculteit" (sommige mensen schreeuwen liever "VIJF!!!")
def factorial( n ):
if n == 1:
return 1
return n * factorial( n - 1 )
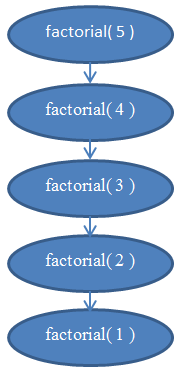
Laten we analyseren de complexiteit van de functie hierboven. De functie heeft geen lussen, maar zijn complexiteit is ook niet constant. Wat we moet doen om de complexiteit ervan te vinden is de instructies tellen. Het is duidelijk dat als we een aantal n aan deze functie doorgeven, deze zichzelf n keer zal uitvoeren. Als je daar niet zeker van bent, voer het dan handmatig uit voor n = 5 om te valideren dat het echt werkt. Als n = 5 bijvoorbeeld, wordt de functie 5 keer uitgevoerd en wordt n bij elke functieaanroep met 1 verlaagd. We zien dus dat deze functie complexiteit Θ (n) heeft.
Als je hier nog steeds niet zeker van bent, probeer dan te onthouden dat we de exacte complexiteit altijd kunnen vinden door het aantal instructies handmatig te tellen. Laten we nu proberen het aantal instructies te tellen dat in deze functie is afgeleid om f (n) te vinden en te bewijzen dat het inderdaad lineair is (onthoud dat lineair Θ (n) betekent).
Zie figuur 5 voor een diagram om de recursies te begrijpen die worden uitgevoerd wanneer faculteit( 5 ) wordt aangeroepen.
Dit moet duidelijk maken waarom deze functie van lineaire complexiteit is.
Logaritmische complexiteit
Een welbekende probleem in informatica is het waarde opzoeken uit een array. We hebben dit probleem eerder opgelost voor een algemene geval. Dit probleem wordt interessant als we een array hebben dat al gesorteerd is en we willen een waarde erbinnen opzoeken. Een methode om dat te doen, wordt binair zoeken of bisectie genoemd. We kijken naar het middelste element van onze array: als we het daar vinden, zijn we klaar. Anders, als de waarde die we daar vinden groter is dan de waarde die we zoeken, weten we dat ons element zich aan de linkerkant van de array zal bevinden. Anders weten we dat het zich aan de rechterkant van de array bevindt. We kunnen deze kleinere arrays in tweeën blijven splitsen totdat we een enkel element hebben om naar te kijken. Hier is de methode in pseudocode gepresenteerd:
def binarySearch( A, n, value ):
if n = 1:
if A[ 0 ] = value:
return true
else:
return false
if value < A[ n / 2 ]:
return binarySearch( A[ 0...( n / 2 - 1 ) ], n / 2 - 1, value )
else if value > A[ n / 2 ]:
return binarySearch( A[ ( n / 2 + 1 )...n ], n / 2 - 1, value )
else:
return true
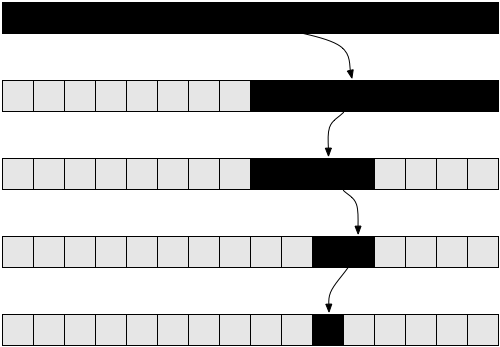
Dit pseudo code is een simplificatie van de echte implementatie. In praktijk is het methode eenvoudiger uitgelegd dan geïmplementeerd, omdat de programmeur enkele implementatieproblemen moet oplossen. Er zijn “off-by-one” fouten en de deling door 2 levert niet altijd een geheel getal op en daarom is het nodig om de waarde door de floor() of ceil() functies te duwen. Maar we kunnen aannemen dat, voor onze doeleinden, het werkt altijd met success en dat onze echte implementatie zorgt voor de off-by-one fouten omdat we willen gewoon de complexiteit van dit methode analyseren. Als je nooit een bisectie heeft geïmplementeerd, je zou dat in je favoriet programmeertaal doen omdat het echt verhelderend is.
Zie figuur 6 om u te helpen begrijpen hoe bisectie werkt.
Als je niet zeker weet of deze methode echt werkt, neem dan even de tijd om deze handmatig uit te voeren in een eenvoudig voorbeeld om je jezelf overtuigen dat het echt werkt.
Laten we nu proberen dit algoritme analyseren. We hebben weer een recursief algoritme. Stel voor de eenvoud dat de array altijd in tweeën wordt gesplitst, waarbij de huidige +1 en -1 in recursie worden genegeerd. Het zou inmiddels duidelijk moeten zijn dat het negeren van -1 en +1 het resultaat van complexiteit niet verandert. Dit is een feit dat we normaal gesproken zouden moeten bewijzen als we voorzichtig willen zijn vanuit wiskundig oogpunt, maar praktisch is het intuïtief duidelijk. Laten we aannemen dat de grootte van onze array precies de graad twee is, om de zaken niet ingewikkelder te maken. Nogmaals, dergelijke aannames veranderen niets aan de eindresultaten van de complexiteit die we moeten verkrijgen. In dit geval zou het ergste geval zijn wanneer de array die we onderzoeken niet de waarde zou hebben waarnaar we op zoek zijn. In dat geval zouden we beginnen met een array van grootte n in de eerste aanroep van de recursie, en dan een array van grootte n / 2 krijgen in de volgende aanroep. Dan krijgen we een array van grootte n / 4 in de volgende recursieve aanroep, gevolgd door een array van grootte n / 8 enzovoort. Over het algemeen wordt onze array bij elke aanroep in tweeën gesplitst, totdat we 1 bereiken. Laten we dus het aantal elementen in onze array voor elke aanroep schrijven:
Merk op dat bij de i-de iteratie, onze array heeft n/2i elementen. Het is omdat bij elke iteratie we in elke iteratie onze array in tweeën snijden, wat betekent dat we het aantal elementen door twee delen. Dit vertaalt zich in het vermenigvuldigen van de noemer met 2. Als we dat i keer doen, krijgen we n / 2i. Nu, dit procedureel gaat door en met elke grotere i krijgen we een kleiner aantal elementen totdat we de laatste iteratie bereiken waarin we nog maar 1 element over hebben. Als we i willen vinden om te zien in welke iteratie dit zal plaatsvinden, moeten we de volgende vergelijking oplossen:
1 = n / 2i
Dit is alleen waar als we de laatste aanroep van de functie binarySearch() hebben bereikt, niet in het algemeen. Dus door hier voor i op te lossen, kunnen we vinden in welke iteratie de recursie zal eindigen. Als we beide zijden met 2i vermenigvuldigen, krijgen we:
2i = n
Nu, deze vergelijking zal u bekend zijn als je de sectie over logaritmen geeft gelezen. Oplossen voor i hebben we:
i = log( n )
Dit vertelt ons dat het aantal iteraties dat nodig is om een binaire zoekopdracht uit te voeren log (n) is, waarbij n het aantal elementen in de originele array is.
Als we erover nadenken, is dit logisch. Laten we bijvoorbeeld zeggen n = 32, dus we hebben een array van 32 elementen. Hoe vaak moeten we het halveren om bij een enkel element te komen? We hebben: 32 → 16 → 8 → 4 → 2 → 1. We hebben dit dus 5 keer gedaan, wat een logaritme is van 32. De complexiteit van het binair zoeken naar gletsjers is dus Θ (log (n)).
Dit laatste resultaat geeft ons de mogelijkheid om binair en lineair zoeken te vergelijken. Het is duidelijk dat log (n) kleiner is dan n, dus het is redelijk om te concluderen dat bisectie een veel snellere methode is om naar een string te zoeken dan lineair zoeken, dus het zou verstandig zijn om strings te sorteren voor efficiënter zoeken.
Vuistregel: Het verbeteren van de asymptotische looptijd van een programma verbetert vaak de uitvoering aanzienlijk, veel meer dan enige minder "technische" optimalisatie, zoals het gebruik van een snellere programmeertaal.
Optimaal sorteren
Gefeliciteerd! Je weet nu over analyse van het complexiteit van je algoritmen, de asymptotische gedrag van functies en het Big-O notatie. Je weet ook intuïtief te achterhalen dat de complexiteit van een algoritme O(1), O(log(n)), O(n), O(n2) enzovoort is. Je kent de symbolen o, O, ω, Ω en Θ en ook wat worst-case analyse betekent. Als je zo ver bent gekomen, heeft deze tutorial met succes zijn doel bereikt.
Deze laatste sectie is onverplicht. Het is beetje meer ingewikkeld, dus sla vrij over als je zo voelt. Voor de volgende sectie is het nodig om te focussen en wat tijd met oefeningen doorbrengen. Het zal u echter een zeer nuttige methode bieden bij de analyse van de complexiteit van algoritmen, dus het is zeker de moeite waard om te begrijpen.
We keken naar selectie sortering hierboven. We hebben vermeld dat selectiesortering niet optimaal is. Een optimaal algoritme lost een probleem op de best mogelijke manier op, wat betekent dat hier geen betere algoritmen voor zijn. Dit betekent dat alle andere algoritmen voor het oplossen van dat specifieke probleem een slechtere of gelijke complexiteit hebben in vergelijking met dat optimale algoritme. Er kunnen veel optimale algoritmen zijn voor een probleem die allemaal dezelfde complexiteit hebben. Het probleem met sorteren kan verschillende optimale oplossingen hebben. We kunnen hetzelfde idee gebruiken als bij bisectie om snel te sorteren. Deze sorteermethode heet mergesort.
Om mergesort te doen, moeten we ten eerste een helpfunctie maken die we dan zullen gebruiken om de eigenlijke sortering uit te voeren. We zullen een merge functie maken die twee arrays neemt die beide al gesorteerd zijn en ze samenvoegt tot een grote gesorteerde array. Dit is eenvoudig te doen:
def merge( A, B ):
if empty( A ):
return B
if empty( B ):
return A
if A[ 0 ] < B[ 0 ]:
return concat( A[ 0 ], merge( A[ 1...A_n ], B ) )
else:
return concat( B[ 0 ], merge( A, B[ 1...B_n ] ) )
De concat functie neemt een element, de “hoofd” en een array, de “staart”, en bouwt en retourneert een nieuwe array die het "head" -item bevat als het eerste ding in de nieuwe array en het "tail" -item als de rest van de elementen in de array. Bijv. concat( 3, [ 4, 5, 6 ] ) retourneert [ 3, 4, 5, 6 ]. We gebruiken A_n en B_n om de grootte van respectievelijk de arrays A en B aan te duiden.
Oefening 8
Verifieren dat de bovenstaande functie echt een samenvoeging uitvoert. Herschrijf het in uw favoriete programmeertaal met iteraties (met for loops) in plaats van met recursie.
Analyse van dit algoritme laat zien dat het een looptijd heeft van Θ( n ), waarbij n de lengte is van de resulterende array (n = A_n + B_n).
Oefening 9
Verifieren dat de looptijd van merge Θ( n ) is.
Met behulp van deze functie kunnen we een beter algoritme bouwen voor het sorteren. Het idee is als volgt: we splitsen de array in twee delen. We sorteren elk van de twee delen recursief, waarna we de twee gesorteerde arrays samenvoegen tot één grote array. In pseudocode:
def mergeSort( A, n ):
if n = 1:
return A # it is already sorted
middle = floor( n / 2 )
leftHalf = A[ 1...middle ]
rightHalf = A[ ( middle + 1 )...n ]
return merge( mergeSort( leftHalf, middle ), mergeSort( rightHalf, n - middle ) )
Deze functie is moeilijker te begrijpen dan wat we eerder hebben gedaan, dus de volgende oefening kan even duren.
Oefening 10
Verifieren de correctheid van mergeSort. D.w.z. controleer dat de mergeSort, zoals hierboven gedefinieerd, de gegeven string echt correct sorteert. Als je problemen hebt om te begrijpen waarom het werkt, probeer het dan met een kleine voorbeeld array en voer het handmatig uit. Wanneer u deze functie handmatig uitvoert, zorg er dan voor dat leftHalf en rightHalf zijn wat u krijgt als u de array ongeveer in het midden splitst. Het hoeft niet precies in het midden te zijn als de array een oneven aantal elementen heeft (daar wordt de floor functie boven voor gebruikt).
Als laatste voorbeeld zullen we de complexiteit van de functie mergeSort analyseren. Voor elke stap van de functie mergeSort verdelen we de string in twee gelijke delen, zoals bij binarySearch. In dit geval behouden we echter beide helften tijdens de uitvoering. Vervolgens passen we het algoritme recursief in elke helft toe. Nadat de recursie terugkeert, passen we de merge functie toe op het resultaat, dat complexiteit Θ (n) heeft.
Dus splitsen we de originele array in twee array, elk met maat n/2. Vervolgens voegen we deze arrays samen, wat een functie is die n elementen met elkaar verbindt en dus Θ (n) complexiteit heeft.
Zie figuur 7 om recursie te begrijpen.
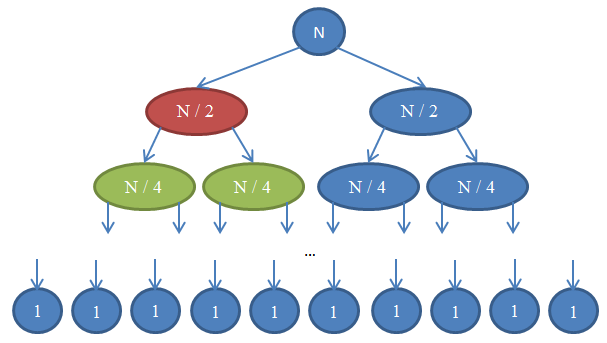
Laten we eens kijken wat hier aan de hand is. Elke cirkel is een aanroep van de mergeSort functie. Het getal in de cirkel geeft de grootte van de array aan die wordt gesorteerd. De bovenste blauwe cirkel is de originele oproep tot mergeSort, waarbij we een array sorteren met de grootte n. De pijlen geven recursieve aanroepen aan tussen functies. De originele aanroep van mergeSort maakt twee aanroepen van mergeSort op twee arrays, elk van grootte n/2. Dit wordt aangegeven door de twee pijlen bovenaan. Elk van deze aanroepen doet op zijn beurt twee eigen aanroepen om samen te mergeSort twee arrays van grootte n/4 elk, enzovoort totdat we bij arrays van grootte 1 aankomen. Dit diagram wordt een recursieboom genoemd, omdat het illustreert hoe de recursie zich gedraagt en eruitziet als een boom (de wortel staat bovenaan en de bladeren onderaan, dus in werkelijkheid ziet het eruit als een omgekeerde boom).
Merk op dat op elke array in het bovenstaande diagram het totale aantal elementen n is. Om dit te zien, bekijkt u elke array afzonderlijk. De eerste array bevat slechts een aanroep naar mergeSort met een array met grootte n, dus het totale aantal elementen is n. De tweede array heeft twee aanroepen van mergeSort elk met de grootte n/2. Maar n/2 + n/2 = n en dus ook in deze array is het totaal aantal elementen n. In de derde array hebben we 4 aanroepen, die elk worden toegepast op een array met de grootte van n/4, wat een totaal aantal elementen oplevert gelijk aan n/4 + n/4 + n/4 + n/4 = 4n/4 = n. Dus opnieuw krijgen we n elementen. Merk nu op dat bij elke array in dit diagram de beller een merge moet uitvoeren op de elementen die door de callees worden geretourneerd. De rode cirkel moet bijvoorbeeld n/2 elementen sorteren. Om dit te doen, splitst het de array met een grootte van n/2 in twee arrays met elk een grootte van n/4, roept mergeSort recursief aan om die te sorteren (deze aanroepen zijn groene cirkels) en voegt ze vervolgens samen. Deze merge operatie vereist het samenvoegen van n/2 elementen. Op elke array in onze boom is het totale aantal samengevoegde elementen n. In de array die we zojuist hebben onderzocht, voegt onze functie n/2 elementen samen en de functie aan de rechterkant (die in blauw staat) moet ook n/2 eigen elementen samenvoegen. Dat levert in totaal n elementen op die moeten worden samengevoegd voor de array waar we naar kijken.
Door dit argument is de complexiteit voor elke rij Θ(n). We weten dat het aantal rijen in dit diagram, ook wel de diepte van de recursie boom genoemd, log(n) zal zijn. De argumentatie hiervoor is precies dezelfde als die we gebruikten bij het analyseren van de complexiteit van bisectie. We hebben log(n) rijen en elk daarvan is Θ(n), daarom is de complexiteit van mergeSort Θ(n * log(n)). Dit is veel beter dan Θ(n2) en dat is wat selectie sort ons gaf (onthoud dat log(n) veel kleiner is dan n, en dus is n * log(n) veel kleiner dan n * n = n2). Als dit ingewikkeld voor je klinkt, maak je geen zorgen: het is niet gemakkelijk de eerste keer dat je het ziet. Kom een paar keer terug naar dit gedeelte en lees het opnieuw nadat je mergeSort in je favoriete programmeertaal hebt geimplementeerd en hebt gevalideerd dat het werkt.
Zoals je in dit laatste voorbeeld hebt gezien, stelt analyse van complexiteit ons in staat om algoritmen te vergelijken om te zien welke beter is. Onder deze omstandigheden kunnen we er nu vrij zeker van zijn dat merge sort een betere selection sort zal uitvoeren voor grote arrays. Deze conclusie zou moeilijk te trekken zijn als we niet de theoretische achtergrond hadden van het analyseren van algoritmen die we hebben ontwikkeld. In de echte wereld worden inderdaad sorteren algoritmen voor looptijd Θ(n * log(n)) gebruikt. De Linux kernel gebruikt bijvoorbeeld heapsort, een sorteren algoritme dat dezelfde looptijd heeft als mergesort (namelijk Θ(n log(n))) dat we hier hebben onderzocht en dus zeer optimaal is. Merk op dat we niet hebben bewezen dat deze sorteren algoritmen optimaal zijn. Dit vereist een iets meer ingewikkelde wiskunde, maar je kunt er zeker van zijn dat als het om complexiteit gaat, deze niet beter kunnen.
Na het lezen van deze tekst, zou de intuïtie voor analyse van algoritmische complexiteit die je hebt ontwikkeld, je moeten helpen om snellere programma's te ontwerpen en je te concentreren op het optimaliseren van zeer belangrijke dingen in code in plaats van triviale dingen, waardoor je de kans krijgt om productiever te zijn. Trouwens, de wiskundige en professionele taal en het vocabulaire zoals de Big-O notatie die je uit de tekst hebt geleerd, kunnen nuttig zijn in de communicatie met andere softwareontwikkelaars als je wilt discussiëren over de looptijd van algoritmen, wat je hopelijk kunt doen met je nieuwe vaardigheden.
Over deze tekst
Dit artikel is gelicentieerd onder Creative Commons 3.0 Attribution. Dit betekend dat je kan het kopiëren en plakken, delen, op je eigen website posten, veranderen, en doe in het algemeen wat je wilt, op voorwaarde dat je mijn naam noemt. Hoewel u niet verplicht bent, als u mijn werk als basis voor uw eigen werk gebruikt, moedig ik u aan om uw eigen geschriften onder Creative Commons te publiceren, zodat het voor anderen gemakkelijker is om te delen en ook samen te werken. Evenzo moet ik het werk dat ik hier heb gebruikt, toeschrijven. De handige iconen die je op deze pagina ziet zijn de fugue icons. Het mooie streeppatroon dat je in dit ontwerp ziet is ontworpen door Lea Verou. En, nog belangrijker, de algoritmen die ik ken, zodat ik dit artikel kon schrijven, werden onderwezen door mijn professoren Nikos Papaspyrou en Dimitris Fotakis.
Ik werk momenteel aan een doctoraat in cryptografie aan de Universiteit van Athene. Op het moment van schrijven was ik een bachelor in elektrotechniek en informatica aan het Nationaal Technisch Instituut in Athene, waar ik aan software werkte, en ik was een coach bij de Griekse competitie van Informatica. Wat de industrie betreft, heb ik als lid van het ontwikkelingsteam gewerkt waar we deviantART hebben gebouwd, een sociaal netwerk voor artiesten. Ook werkte ik bij de beveiligingsteams van Google en Twitter, en bij twee start-ups, Zino en Kamibu, waar we respectievelijk sociale netwerken en videogames ontwikkelden. Je kunt me volgen op twitter en op github. U kunt mij een e-mail sturen als u wilt dat wij contact met u opnemen. Je kunt me ook een e-mail sturen als je de tekst in je moedertaal wilt vertalen, zodat meer mensen het kunnen lezen.
Bedankt voor het lezen. Ik heb geen geld verdiend met het schrijven van deze tekst, dus als je dit leuk vond, stuur me dan een welkomstmail. Ik ontvang graag foto's van plaatsen over de hele wereld, dus voeg een foto van jezelf toe in jouw stad!
Referenties en literatuur
- Cormen, Leiserson, Rivest, Stein. Introduction to Algorithms, MIT Press.
- Dasgupta, Papadimitriou, Vazirani. Algorithms, McGraw-Hill Press.
- Fotakis. Course of Discrete Mathematics at the National Technical University of Athens.
- Fotakis. Course of Algorithms and Complexity at the National Technical University of Athens.

